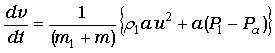エクセルで解く!ロケットの飛ぶ原理
(visitor
since 2004.6.30)
このページの感想をお寄せください。
ファイルをダウンロードしたら、メールくださいね。励みになりますので(^^)。
nozomu@asahi-net.email.ne.jp
§1 連続して銃を撃つ場合を考えてみよう!
台車に乗っている人が、連続して銃を撃つ場合を考えてみよう。
台車は、弾丸を発射する反動で、だんだん加速されます。
これが、まさに、ロケットの推進力の原理です!
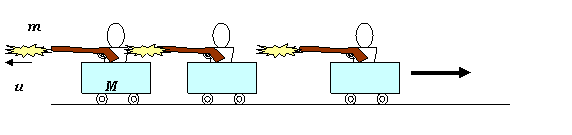
質量mの弾丸に速さu(銃に対する弾丸の速度)を与えることで、台車の速度がV からV+ΔV に変化したとしましょう。
地面に対する弾丸の速度をv とすれば、-u=v-Vであり、
また、運動量保存の法則より、
MV=mv+(M-m)(V+ΔV) がなりたつので、
=m(V-u)+(M-m)(V+ΔV)
これを整理して、
ΔV=mu/(M-m)
となります。1回の弾丸の発射で、台車がどれだけの速度を得るかが計算できるわけです。
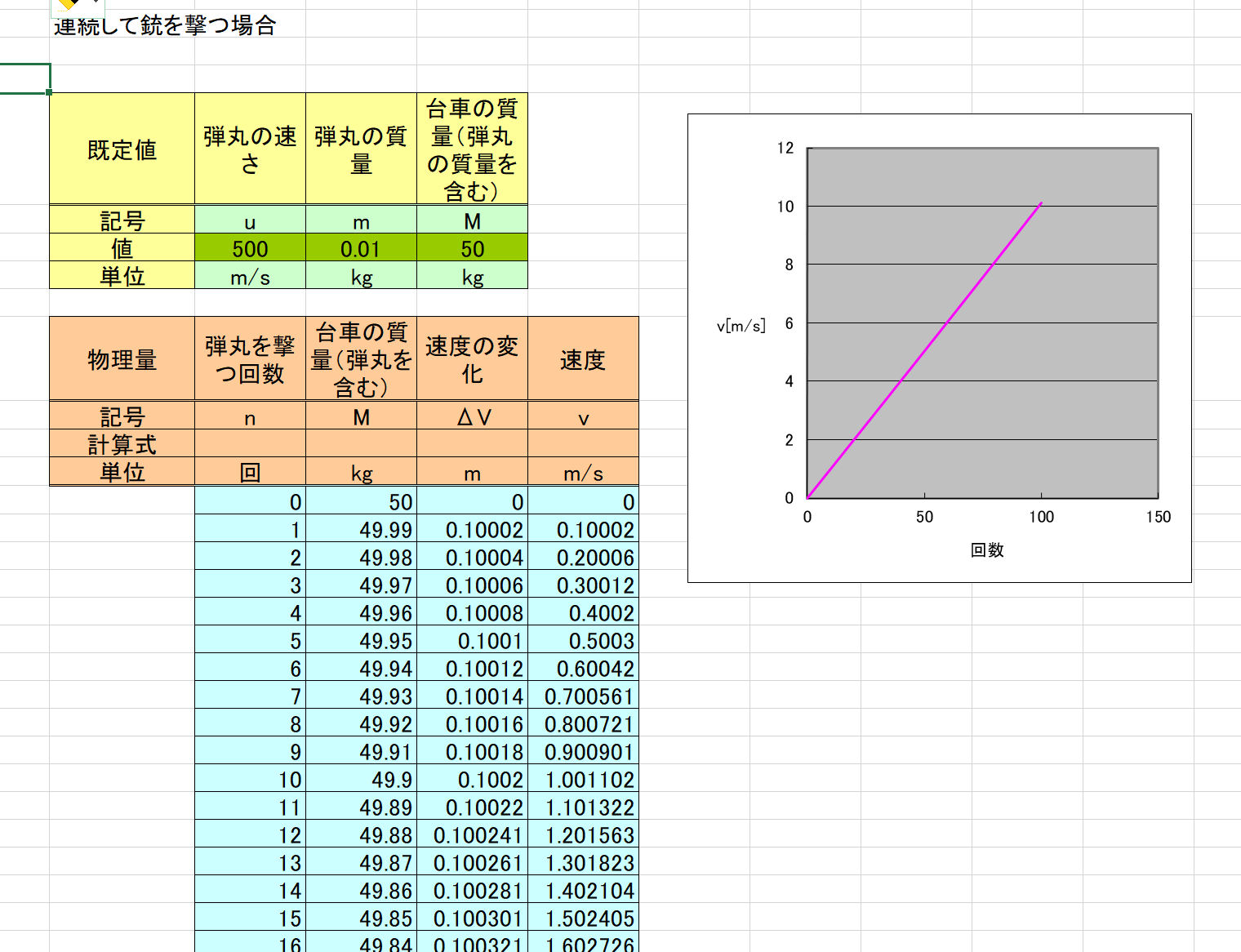
台車の速度がどのように変化するか、エクセルで計算してみましょう。
弾丸を重くしたり、軽くしたり、いろいろ変えて、台車の速さの変化を調べてみよう。
(下のファイルをダウンロードしてください)
![]() dangan1.xls ・・・・・・・・・・・・download
dangan1.xls ・・・・・・・・・・・・download ![]()
10gの弾丸を500m/sで100発撃った場合で計算してみました。
§2 連続してガスを放出するロケットエンジンの推力とは!

ロケットが、毎秒、質量βのガスを、ロケットに対して、uの速さで噴出しているとしましょう。
微小な時間Δt間に、ロケットの速さがV からV+ΔVに変化したとします。
ロケットが噴出するガスはβ・Δtなので、§1の議論と同じ要領で、
運動量保存の法則より、
MV=βΔt(V-u)+( M-βΔt)(V+ΔV)
ここでΔt×ΔVの項は無視して整理すると、
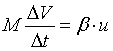 ・・・・・(1)
・・・・・(1)
これは、ロケットの運動方程式を表していますね。右辺は、ロケットにはたらく力すなわち推力を与える式です。
また、噴出したガスの圧力Peが大気圧Poより高いときは、ロケットには、圧力推力と呼ばれる力が作用します。(文献5)
これは、また後で議論することにします。
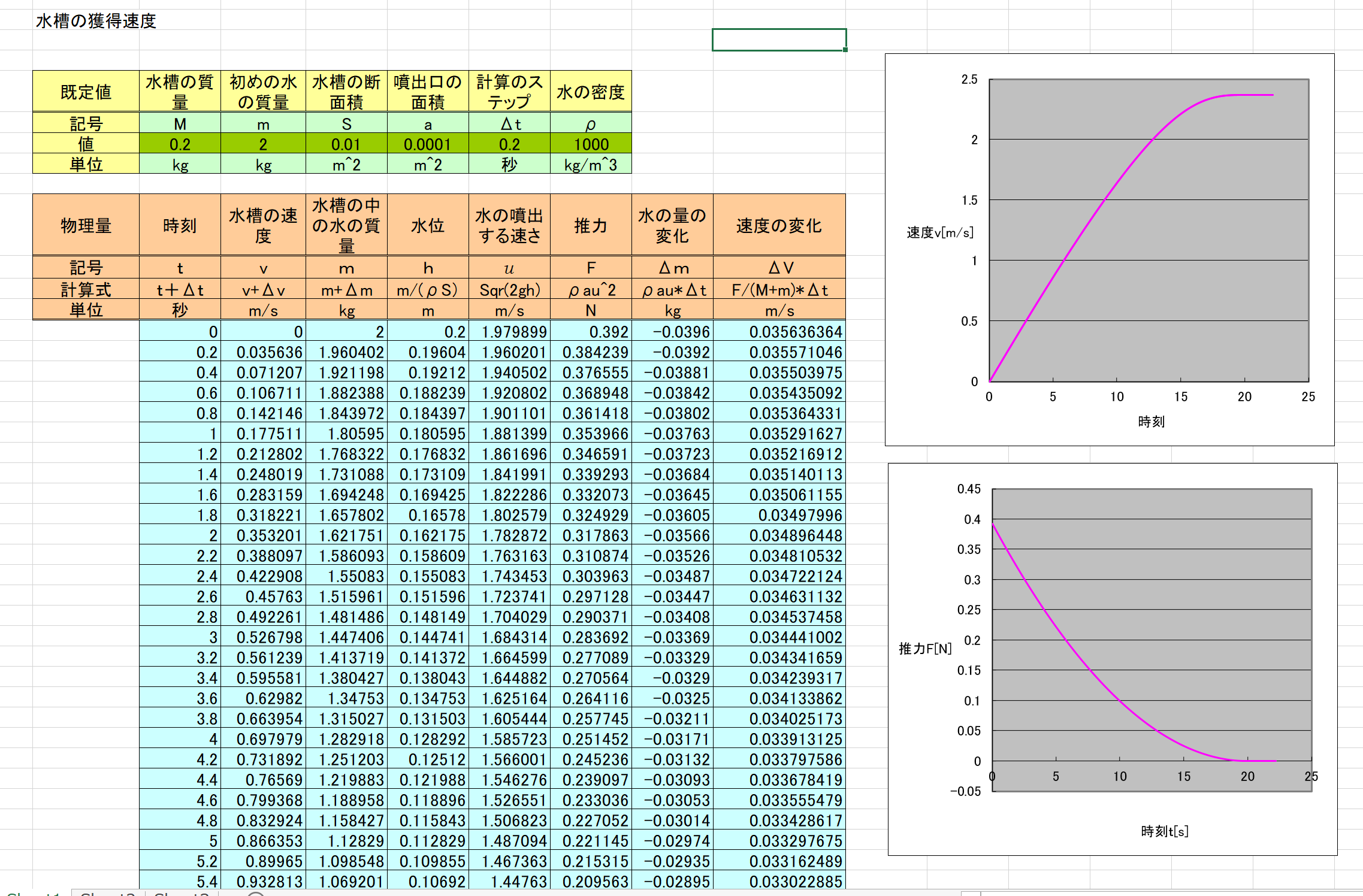
§3 水を噴出するときに得る推力とは!
今、水槽に、水が入っていて、小さな穴から水が噴出しているとしましょう。
水が噴出することで、水槽は推力を得て、加速されていきます。
水が全部出てしまうまでに、水槽がどれだけの速さになるのか(獲得速度)を計算してみましょう。
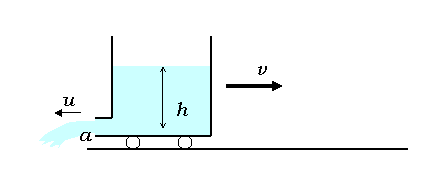
このとき、噴出する水は、水槽に対して、uの速さであるとすると、
![]() ・・・(2)
・・・(2)
となることがわかっています。(文献6)
推力Fは、(1)より、
F=β・u
でしたが、βは
β=ρa・u
とあらわされます。
(ここで、aは、水の噴出する穴の面積、ρは水の密度です。)
そこで
![]()
とあらわされます。
よって、水槽の運動方程式は
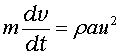 ・・・(3)
・・・(3)
ここで、m
は時間t の関数です。(水が噴出すれば、m は減少します。)
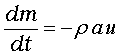 ・・・(4)
・・・(4)
さて、(2)、(3)、(4)式をエクセルで解いてみましょう。(下のファイルをダウンロードしてください)
![]() waterjet1.xls ・・・・・・・・・・・・download
waterjet1.xls ・・・・・・・・・・・・download ![]()
§4 ガスを噴出するときの推力の計算!(ちょっと難しい)
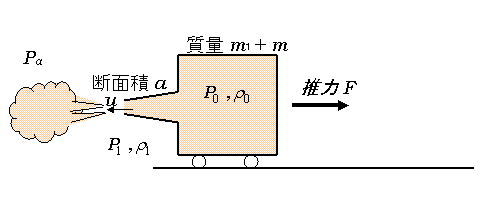
今、断熱容器の中に、圧力P0、密度ρ0のガスが入っており、このガスを圧力Paの外部へ噴出することによって、推力Fを得ているとしましょう。容器の質量をm1、内部のガス質量をmとします
ガスは噴出口(断面積a)で膨張し、圧力がP1、密度がρ1 になったとします。
ここで、噴出口での圧力は、外気圧Paと必ずしも一致していないことに注意が必要です。
さて、噴出するガスの流速uは、
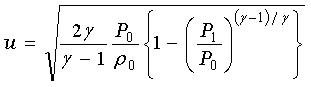 ・・・(5)
・・・(5)
となることがわかっています。(文献8)
ここで、γはこのガスの比熱比を表しています。
ここで、質量流量(単位時間あたりの噴出ガスの質量)βを考えてみましょう。
![]() に、
に、
(5)式と、断熱変化の式
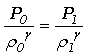 ・・・(6)
・・・(6)
を用いて整理すると、
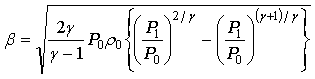 ・・・(7)
・・・(7)
が得られます。 (文献8)
さて、このβの式を吟味してみましょう。
今、容器が十分に大きく、ガスが少々噴出しても、内部の圧力が保たれているとします。そこで外気圧Paの値を内部の圧力P0より徐々に下げていき、ガスを外へ噴出させたとしましょう。ここで、P1とPaの関係に注意が必要です。初めは外気圧Paを下げれば、P1がPaと同じ値まで下がります。初めのうちはP1=Paです。
外気圧を下げるほど噴出するガスの速さは速くなると想像できると思いますが、流量βには限界値が存在します。
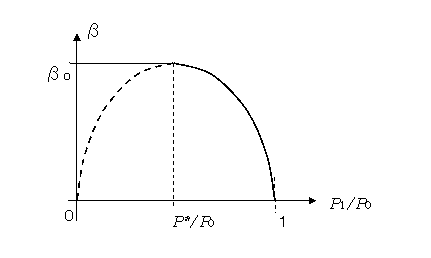
(6)式をグラフにしてみると、P1 の値を下げていくと、P*となった時点でβは最大値となります。このP*の値からいくら外気圧をPa下げても、P1 の値はP*のままでそれ以下にはならず、βはβ0から増えません。(グラフでは点線のようにβが下がっていきますが、現実はβの値は変化しない)。この状態を流れの閉塞(チョーキング)といい、外気圧が変化しても流量が一定になる状態です。実はこのとき、ガスの流れの速さが音速に等しくなっています。(文献8)
(噴出するガスは外気から、圧力の低さで引っ張り出されているわけですが、P*の値以下に外気圧を下げても、その圧力の情報が容器の内部に伝わらないのです。この引っ張る力が内部の気体に音速でしか伝わらないので、これ以上速く引っ張り出せないということでしょうか=筆者の解釈)
ここで、P*の値は、
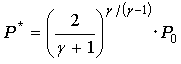
です。(文献8)
γ=1.4として計算すると、
![]()
となるので、おおざっぱに言って、容器の中の圧力が外気圧より2倍以上あれば、閉塞状態となります。
さて、それでは、この容器の運動方程式ですが、
式(1)で議論した推力βu は運動量推力と呼ばれますが、
噴出口での圧力P1 がPa まで下がらないとき(閉塞状態のとき)は、
圧力推力 a(P1- Pa)が加わります。(文献5)
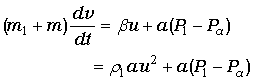 ・・・(8)
・・・(8)
ここで、m
は時間t とともに変化します。(ガスが噴出した分、m は減少)
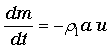 ・・・(9)
・・・(9)
uは、(5)式の通り、容器内部のガスの圧力P0 と P1の関数です。
P1 の値は、閉塞していないときは外気圧Paに等しく、
閉塞状態のときは、P* に等しいと考えます。つまり、
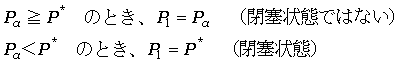
として、(5)式に代入し、u を求めることになります。
また、ρ1の値は、(6)式を変形した次式で求めて代入します。
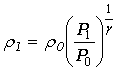 ・・・(10)
・・・(10)
また、容器内の圧力P0の値は、ガスを噴出するにつれ下がっていきます。
このP0 の変化を微分方程式にしてみましょう。
ガスが噴出し内部のガスの質量が Δm 変化したことで、
容器の内部のガスの密度が Δρ0 変化したとすると、
容器の体積を Vとして、密度が m/V であることから、
![]()
また、 (9)式より、![]() なので
なので
![]() ・・・(11)
・・・(11)
また、断熱変化の式より、
内部のガスの密度の変化を Δρ0 と圧力の変化を ΔP0 として
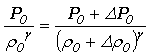
これを変形して
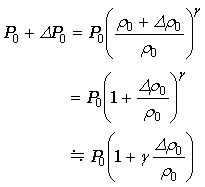
この式を整理して、
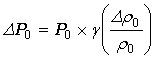 ・・・(12)
・・・(12)
ここで、(11)式より、
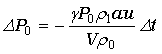 ・・・(13)
・・・(13)
よって、
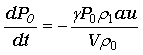 ・・・(14)
・・・(14)
それでは、この容器の運動を解析する式をまとめてみましょう。
(8)、(9)、(14)、(5)、(10)、などから
|
ここで、
また、P1 の値は、
ここで、P* とは
|
以上です。
それでは、準備ができましたので、これらの式をエクセルで解いてみましょう。
![]() gas_jet1.xls ・・・・・・・・・・・・download
gas_jet1.xls ・・・・・・・・・・・・download ![]()
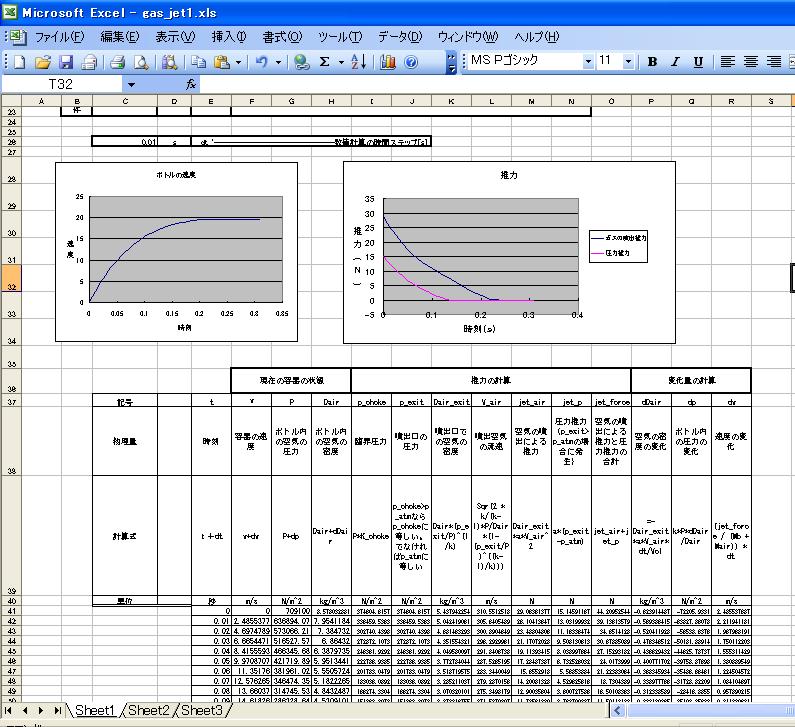
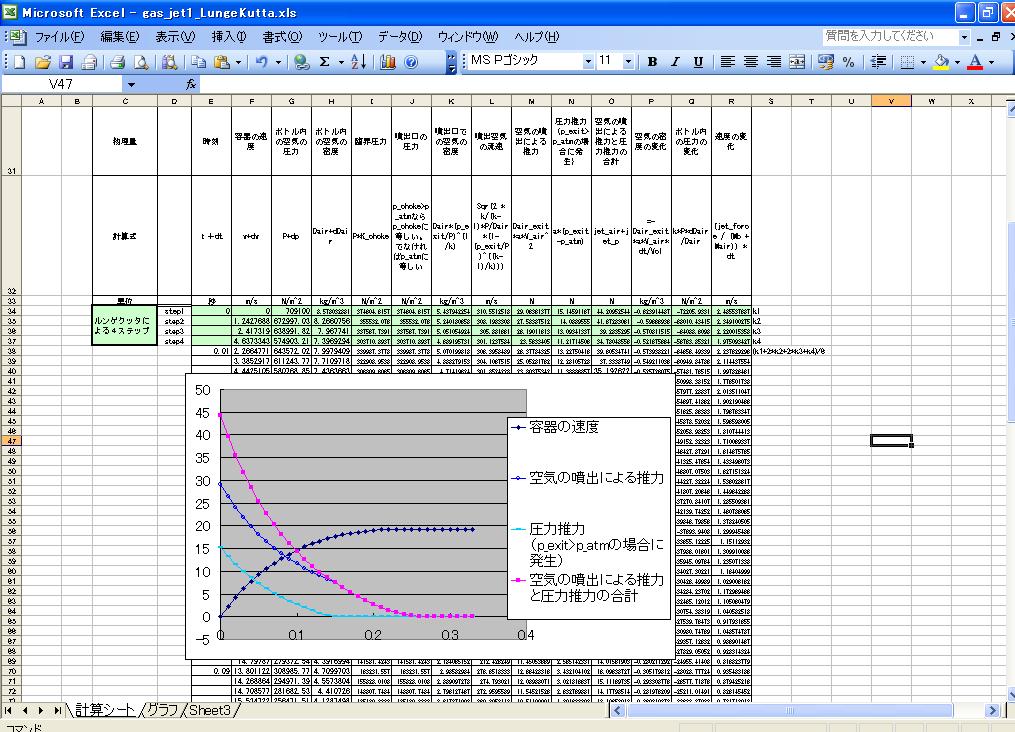
ルンゲクッタでシミュレーションしてみました。
![]() gas_jet1_LungeKutta.xls ・・・・・・・・・・・・download
gas_jet1_LungeKutta.xls ・・・・・・・・・・・・download
まだまだつづく。
まだまだ工事中です。
![]() 工事中
工事中
5 やってみよう! ペットボトルロケットの推力の計算!
軌道計算の方法をアップロードしました。
ペットボトルロケットの力学(全面改訂版)
(2020.8.1)
![]()