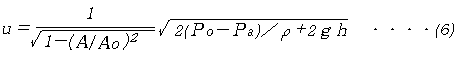 となる7)。
となる7)。これを推力Fの式に代入すれば推力は
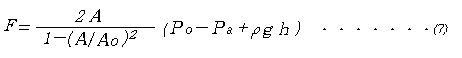 となる。近似的には、F=2A(P0-
Pa)としてもよい。
となる。近似的には、F=2A(P0-
Pa)としてもよい。圧力タンク内の圧力P0は水の噴出に伴い急激に減少するが、この変化は断熱変化とみなし計算すればよい。
ペットボトルロケットの推力には、水の噴出によるものと、水がなくなった後に起きる空気の噴出によるものとがある。
まず、水の噴出によって得られる推力を考える。水(密度ρ)を、断面積A の口からロケットに対し速さ u で噴出するとき、微小時間 dt 間に噴出する水の質量dmは、
dm=ρ A u・dt -------(1)
となる。dmがロケットからuの速さで後方に噴射されたことで、ロケットの受けた力積F・dtは
F・dt = dm・u -------(2)
となり、これに前式を代入し整理すれば、ロケットの推力Fの式、
F=ρA u2 -------(3)
が得られる6)。
流体力学の基礎式であるベルヌーイの式および連続の式より、
(1/2)・ρu2+Pa =(1/2)・ρu02+ρg h+P0 -------(4) u・A=u0・A0 -------(5)
がなりたつ。ここでPaは大気圧、P0は圧力タンク内の圧力である。gは重力加速度、hは噴射口からタンク内の水面までの高さである。この2式から、
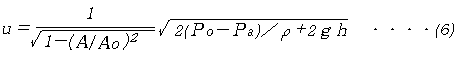 となる7)。
となる7)。
これを推力Fの式に代入すれば推力は 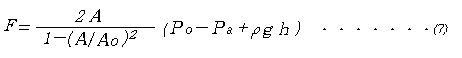 となる。近似的には、F=2A(P0-
Pa)としてもよい。
となる。近似的には、F=2A(P0-
Pa)としてもよい。
圧力タンク内の圧力P0は水の噴出に伴い急激に減少するが、この変化は断熱変化とみなし計算すればよい。
水の噴出が終わった時点で、圧力タンク内にはまだ圧縮空気が残っている。この空気が噴出することにより、ロケットは推力を得てさらに加速されることになる。
空気の圧力、密度がP0、ρ0であるタンク内から、圧力Paの外気に流出する場合を考える。噴出口で気体の圧力、密度がそれぞれP1、ρ1とすれば、噴出口での流出速度u1は、圧縮性流体の式より、
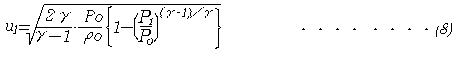
γは空気の比熱比でγ=1.4を代入し整理すれば、

と表される8)。
ここで、噴出口での圧力P1は外気圧Paと等しいとは限らない。噴出する気体の流速u1が音速を超えていないときは、噴出口圧力P1は外気圧Paにほぼ等しいと考えてよい。
しかし、内外の圧力差が大きくなるとともに、流速が増しても、流速は音速の壁を乗り越えることができないので、噴出口圧力P1は外気圧Paまで下がらず、
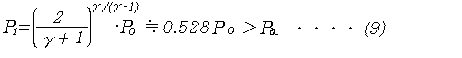
となる。このような状態をチョーキング(流れの閉そく)という7)8)。
噴出空気に与える運動量の反作用としての推力Faは、水の噴出の場合と同じようにρ1・A・u12
となり、また断熱膨張の式ρ1=ρ0・(P1/P0)(1/γ)
を用いることで、
Fa=ρ1・A・u12=7・A・P1・{ (P0/P1)(2/7)-1 } -------(10)
となる。また、空気の噴出口圧力が大気圧より大きいときには、
これに圧力の差からくる推力 Fp
(圧力推力という)
Fp= A(P1−Pa) -------(11)
が加わる5)。
まとめると、推力Fは
F=Fa+Fp=7AP1・{ (P0/P1)(2/7)-1 }+ A・(P1−Pa) -------(12)
となり、ここで、P1については
0.528×P0≧Paのとき、P1=0.528×P0 0.528×P0<Paのとき、P1=Pa
を代入する。
「§5.パソコンによるシミュレーション」へ
|