分数の割り算って小学校の時習いましたよね。私は“おもひでぽろぽろ”のタエ子のように、分数を分数で割るって事がさっぱりわかりませんでした。ただ答えを出すには、ひっくり返して掛け算をすればいいと単純に覚えたわけです。それからずぅ〜っと事あるたびに、分数で割るってどういうことだろうと悩んでました。

　先日、姪っ子が夏休みの宿題をしていて、やはり分数の割り算をしていました。分数の割り算ってどういうことか、またまた気になって、たまたま下のような図を描いてみました。これもたまたま　６分の１÷３分の１　を思いついて…



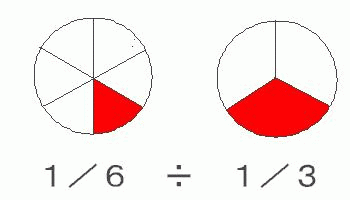
　「そうか！」ってこの時思いました。６分の１にしたもの（１／６の赤い部分）を割ろうとしていたからおかしくなってたんですね。“÷”の意味をBをAにするにはどうしたらいいのかと考えればいいわけです。この場合、“１／３を１／６にするにはどうしたらいいのか”、つまり１／２（＝半分）にすればいいわけですね。これが答え。

　６÷３を考えればもっとわかりやすくなります。“３を６にするにはどうしたらいいのか”。２倍にすればいい。つまり答えは２。

　25年ぐらい悩んでいた頭がやっとすっきりしました。きっとこんな事当たり前じゃん！って方、多いでしょうが、私にはもう最高の発見でした。

I could not understand the meaning of division of fraction for a long time. For example, 1/6 ÷ 1/3. This fractional expression means, I thought, that 1/6 should be dividened to make it smaller than 1/6. But when I drew the above schematic, I had one idea. I should not do anything to 1/6. I must make 1/6 using 1/3 ! I say, "what should 1/3 be done to make 1/6?" 1/3 should be made half. The answer is 1/2 (= a half).

6÷3 is easier to understand. "What should 3 to be done to make 6?" You must make 6 using 3. Yes, you must multiply 3 by 2. The answer is 2.

My head is clear now.

to Home表紙へ