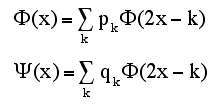
さて、ここまでのところ、Haar以外のウェーブレットについては詳しく触れることを避けてきた。多重解像度解析の概念的説明はHaarウェーブレットでは比較的容易だが、次に簡単な2次のドベシィ(Daubechies)ウェーブレットでさえも格段に見通しが悪くなるようで参考書では数式での説明に終始している。
2次のドベシィウェーブレットでできる限りの説明を試みてみよう。
スケーリング関数φ(x)は以下の関係式で規定されている。
φ(x)=0.683013φ(2x)+1.183013φ(2x-1)+0.316987φ(2x-2)-0.183013φ(2x-3)
マザーウェーブレットψ(x)はスケーリング関数を使って以下の関係式で規定されている。
ψ(x)=-0.183013φ(2x+2)-0.316987φ(2x+1)+1.183013φ(2x)-0.683013φ(2x-1)
右辺の係数は注意深く選ばれたものででたらめな値では使い物にならない。ここでは係数の決め方については触れない。上の式はトゥースケール関係と言われていて、一般的には以下のようにまとめられている。
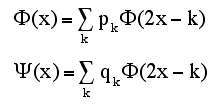
2次のドベシィウェーブレットのスケーリング関数のpはkが0から3までが0ではない値を持ち、それ以外のkでは0となっている。マザーウェーブレットのqはー2から1までが0ではない値を持ち、それ以外のkでは0となっている。これらの係数は、フィルターとして使われているものと同じものだ。
さて、φ(x)はどんな形をしているのだろう。はじめに書かれている書き下した式の方が取りつきやすいとはいえ、どんな形の関数なのか式だけで理解できる人はいないだろう。
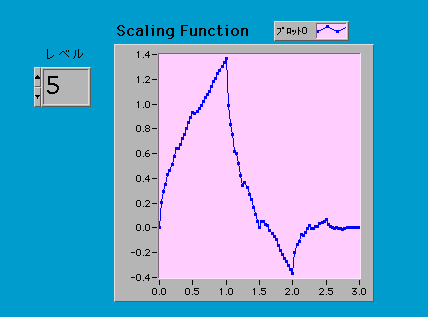
まず、局所的な関数としたときに関数の範囲をチェックしてみよう。x=-1でφ(x)が0以外の値aでx=-2以下ではφ(x)=0だとしよう。x=-1を代入すると、
φ(-1)=0.683013φ(-2)+1.183013φ(-3)+0.316987φ(-4)-0.183013φ(-5)
左辺はa、右辺は0だからaは0になる。こんなやりかたで確認していくと0と3に挟まれた狭い範囲でしか値を持たないことがわかる。
φ(0)=0.683013φ(0)+1.183013φ(-1)+0.316987φ(-2)-0.183013φ(-3)
φ(1)=0.683013φ(2)+1.183013φ(1)+0.316987φ(0)-0.183013φ(-1)
φ(2)=0.683013φ(4)+1.183013φ(3)+0.316987φ(2)-0.183013φ(1)
φ(3)=0.683013φ(6)+1.183013φ(5)+0.316987φ(4)-0.183013φ(3)
φ(0)、φ(1)、φ(2)、φ(3) 以外は関数の範囲外なので消してしまうと、
φ(0)=0.683013φ(0)
φ(1)=0.683013φ(2)+1.183013φ(1)+0.316987φ(0)
φ(2)=1.183013φ(3)+0.316987φ(2)-0.183013φ(1)
φ(3)=-0.183013φ(3)
φ(0)=0、φ(3)=0となる。
φ(1)とφ(2)の式は整理すると
φ(1)=0.683013φ(2)+1.183013φ(1)
φ(2)=0.316987φ(2)-0.183013φ(1)
になってどちらも-0.183013φ(1)=0.683013φ(2)になる。これではまだ決まらないので、もうひとつφ(0)+φ(1)+φ(2)+φ(3)=1という
条件を追加すると次のようになる。
φ(0)=0、φ(1)=1.366026、φ(2)=-0.366026、φ(3)=0
x=0.5での値はいくつになるだろう。
φ(x)=0.683013φ(2x)+1.183013φ(2x-1)+0.316987φ(2x-2)-0.183013φ(2x-3)
にx=0.5を代入すると
φ(0.5)=0.683013φ(1)+1.183013φ(0)+0.316987φ(-1)-0.183013φ(-2)
だからφ(0.5) = 0.683013×1.366026 = 0.933014
このようにスケーリング関数がxと2xの関数になっていることを利用して2分割点での値を次々に求めることができる。
随分細かな手計算が続いてきたので、嫌になった人もいるかもしれないが、ダイアグラムだけではなにをやっているのか分かりにくいので具体的に書いてみた。
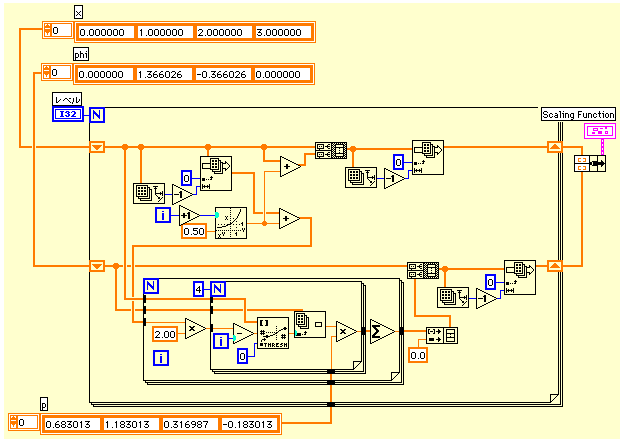
ここまではトゥースケール関係を同じスケールの中での関係と考えて2分割点を増やして関数の形を考えてきた。見方を変えて異なるスケール間の関係式と考えてみる。
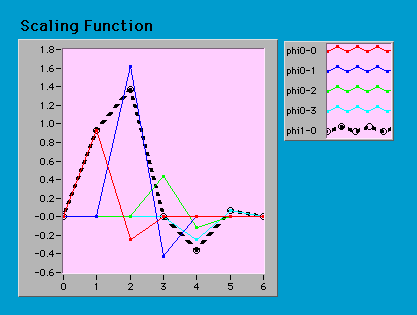
φ(x)=0.683013φ(2x)+1.183013φ(2x-1)+0.316987φ(2x-2)-0.183013φ(2x-3)
右辺は解像度の高いスケールでの4つのスケーリング関数の和であり、左辺は一段階だけ解像度を下げたスケーリング関数である。この状況をグラフで示すと、実線の4つのグラフの合成で解像度の低い(低周波の)破線のグラフになる。
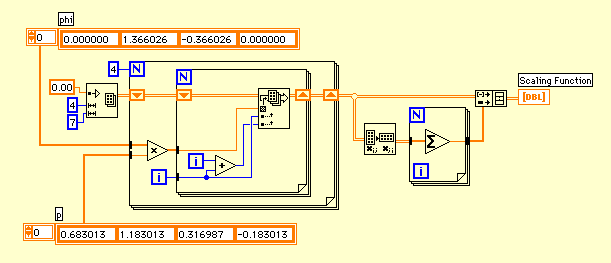
上のダイアグラムのpをqに変更するとウェーブレットのトゥースケール関係で同様の表示を行うことができる。
ψ(x)=-0.183013φ(2x+2)-0.316987φ(2x+1)+1.183013φ(2x)-0.683013φ(2x-1)
ただし、横軸がシフトしていることに注意。
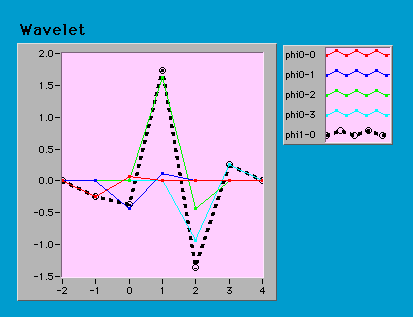
スケーリング関数の線形結合は一段階低解像度のスケーリング関数とウェーブレットに分解できる、というのが離散ウェーブレット変換の要点なのだが本当にできるのだろうか? 基本的な例として、大きさ1のφが1個あったとき、どのように分解されるか計算してみた。低解像度ではφとψ2個ずつに分解された。巧妙に係数が与えられて4〜6列、9〜11列でφとψがキャンセルされている。
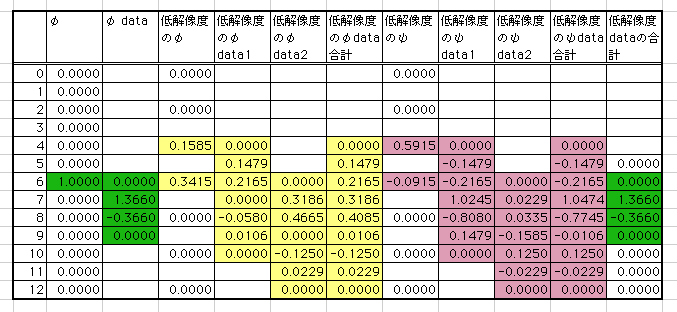
Haarウェーブレットでは分解の様子がわかりやすかったが、関数の形が複雑になっているため分解合成も複雑になっている。
次回は、フィルターによる違い、ノイズ除去、突発的スパイクの検出など、どんな時にウェーブレット解析が役に立つのか見てみよう。