その中で、訂正が一つ。周波数の時間変化を見たいときには『短時間コサイン変換』を使うとグラフィカルに周波数変化を探ることができる、と書いたが、実際にグラフを書くのに使ったのは短時間コサイン変換ではなく、コサインからつくった連続ウェーブレット変換といわなければいけないようだ。その辺の細かいこだわりはウェーブレット変換の利点に直接かかわってくるので次回ぐらいに考えてみたい。
さて、コサイン波形が短時間で減衰するように適当な窓関数をかけたexp(-(x^2/64))*cos(x)を基本に、時間軸を平行移動させるパラメータbと周波数を変化させるパラメータaを導入して次のような関数を考えよう。
F(x,a,b) = exp(-((x-b)/a)^2/64)*cos((x-b)/a)
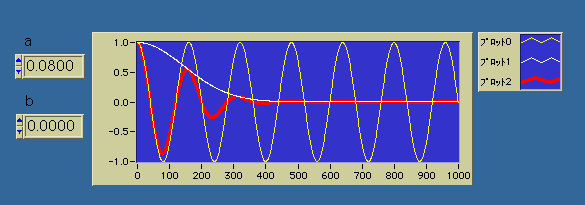
プロット0はcos((x-b)/a)、プロット1はexp(-((x-b)/a)^2/64)、プロット2はexp(-((x-b)/a)^2/64)*cos((x-b)/a)として下のグラフに表示した。

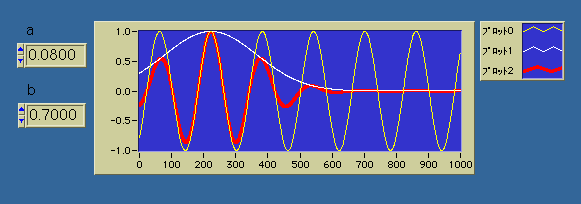
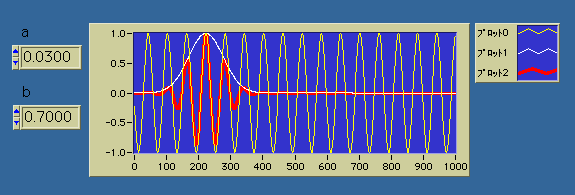
bはトランスレート、aはスケールと呼ばれているが、グラフからイメージが伝わるだろうか?このような小さな(局所的な、短時間の)波の愛称をウェーブレットといっている。周波数が高くなるにつれて窓の幅が狭まってスケールを変えても山谷の数が一定になっていることに注意しよう。
aとbを変化させながら信号とウェーブレットの積を作って数値積分を行うと、信号とウェーブレットの一致度合が高い場合に絶対値が大きな数値になる。下のダイアグラムでは信号をf(x)[0,Pai]という1次元配列に保存しておいて、2重のホワイルループの中で計算を行っている。
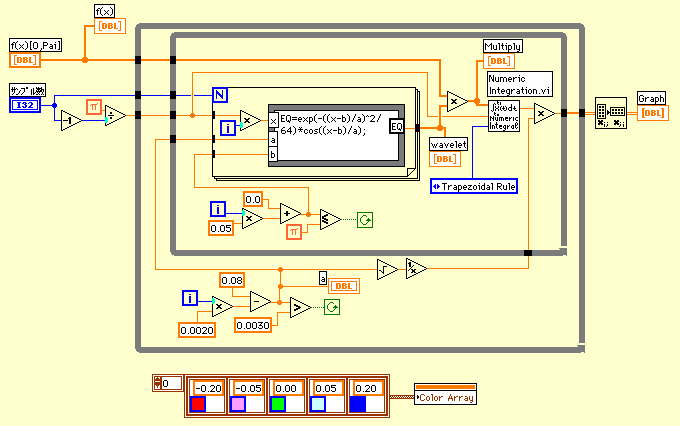
下のグラフは上から信号、ウェーブレット、それらの積の順番になっている。ウェーブレットが移動すると積分値は正負に振れる。
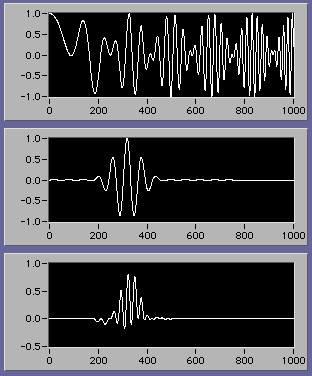
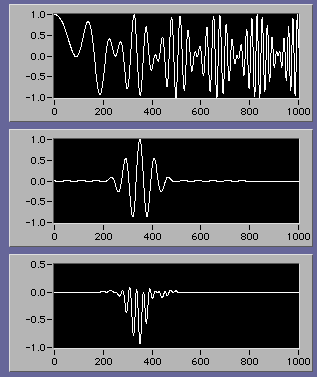
そんなわけで青と赤の縞模様になるのだ。
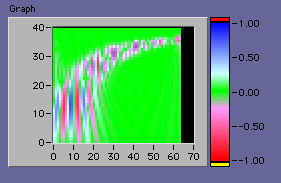
もう少し先まで行きたかったが、今回はここまでとしよう。