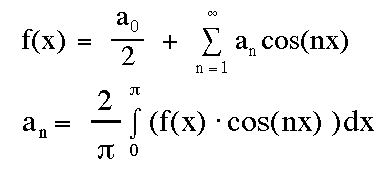
正確な説明を調べてみようと思い、二昔前のテラカン(寺澤寛一)の数学概論を開いてみた。ところどころ今から見るとどうでもいい場所にアンダーラインや書き込みがしてある。当時は本を読んで理解(?)するしか手がなかったが、今はLabVIEWがそばにある。人によってはMathematicaかもしれないが、、、。
フーリエ級数の説明では、だいたい普通の関数(Dirichletの条件を満たす関数と書いてある)だったらフーリエ級数で級数展開ができて、関数がたまたま偶関数だったらサイン成分が消えて定数と定数とコサイン成分だけが残る。これがコサイン変換というものらしい。
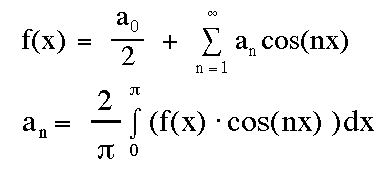
小手調べということで実際にコサイン変換のVIを作ってみた。
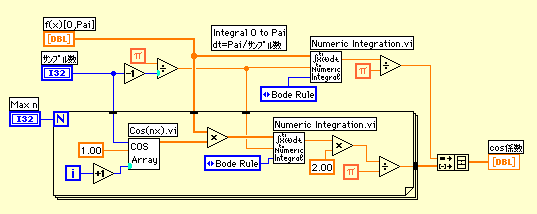
数値積分のviを使うのは初めてだったから少し戸惑ったが、なかなか速くて良い。cos(nx)は信号生成のsin wave.viの位相を変えれば良いと思ったが、どうも三角関数のsine関数を使って作ったものと比べると精度が落ちるようだ。小数点13位以下で違う値を出してくるようなので積分するとちょっと具合が悪い。あまりよくはわからないのだが、今回は三角関数のcosine関数を使って自分でサブviを作ることにした。
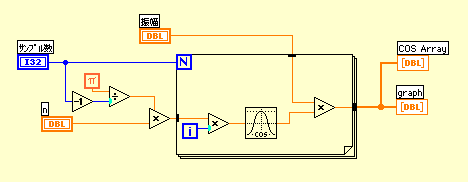
さて、うまく動くか確認してみよう。
f(x)=cos(4x)*cos(11x)という結果の簡単に分かる関数を変換してみよう。0からπまでをサンプル数1000個で入力してみると、結果は7と15で0.5になった。
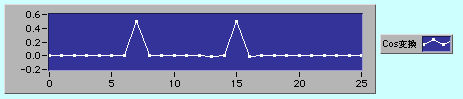
1/2(cos(11x+4x)+cos(11x-4x)) = cos(4x)*cos(11x)
だったよね。n=15のときはf(x)とcos(15x)の山と谷が一致しているからそれらの積(黄色)は下のように正の値になっている。
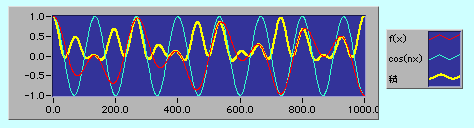
n=14のときはf(x)とcos(15x)の山と谷が徐々にずれて、それらの積(黄色)は下のように正の部分、負の部分が出てきて積分すると計算誤差の範囲でゼロになってしまう。
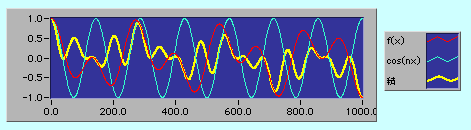
それでは連続的に周波数が変化するような関数ではどんな結果になるのだろう。
f(x)=cos( x )*cos(x^2/2)を例にとって変換してみよう。
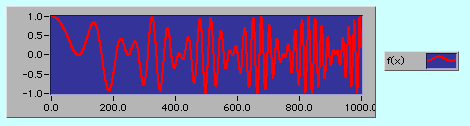
コサイン変換VIで変換すると下のグラフのような結果が得られた。nは110までを計算させた。
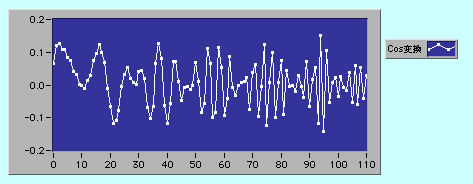
入力波形とかなり似通ったスペクトルが表示された。画像圧縮などで用いられる離散コサイン変換と同じような理屈が働いているのだろう。これはこれで興味深いが、周波数の時間変化を知りたいときにはあまり有効ではない(と思う)。
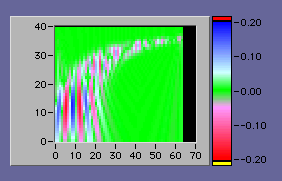
周波数の時間変化を見たいときには短時間コサイン変換を使うとグラフィカルに周波数変化を探ることができる。VIの説明などは次回に回すことになるが、結果だけを示すと下のグラフのようになった。縦軸が周波数、横軸が時間で時間が経つにつれて周波数が高くなっている様子を感覚的に捕らえることができる。
では、次回も気長に待っていてください。