Chapter Eighteen

第18話

さて、前回までで四則演算と１０進数の表現ができあがった。今回は公開鍵暗号方式の鍵となる素数を見つけだす方法について説明しよう。
厳密に素数であることを確認するには今でも「エラトステネスの素数の篩」を使わなくてはならないようだ。この方法は、第１０話で素因数分解をするVIとして紹介した。最小の素数である２からスタートして、２の倍数をすべて消去する。次に消去されていない数（３）を素数としてその倍数をすべて消去する。このような手順で整数を篩にかけて徐々に素数を選び出していく。手順は簡単だが、この方法では探索範囲が広いとメモリが膨大に必要になるのが欠点だ。
第１３話で公開鍵暗号方式の仕掛けを説明したが、その中でつぎの「フェルマーの定理」についてもふれた。
「任意の素数pと任意の整数m ( 1 < m < p ) に対して、
m^(p-1) mod p = 1
が成り立つ。」
逆は真ならずで、pが素数でないときにも成り立つ場合があるため、この関係が成り立っても素数とは決めつけられない。但し、１００桁程度の十分大きな素数の場合、素数でない確率は10^(-13)程度で、たぶん僕のVIにバグがない確率よりも低いため実質的にはあまり気にする必要はないようだ。暗号の本には、ラビンテストという方法でさらに確からしいものにすることができると書いてあるが、今回はパスすることにした。

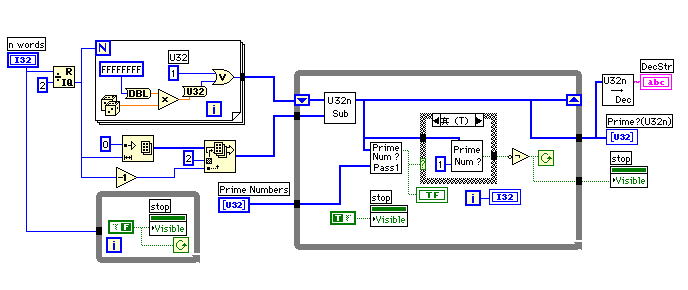
作り出すキー(N)のサイズを入力してその半分の大きさの素数を見つけることにし、探索のスタートポイントを適当な奇数にするため、左上のフォーループでランダムな数のビット０を１にして必要な大きさの配列をつくった。右側のホワイルループでは２段階に分けて素数の判定をおこなう。素数でない場合は２を引いて素数が見つかるまで繰り返す。パス１は「エラトステネスの素数の篩」で作った約350個の素数で割り切れないことを確認する。パス２では、「フェルマーの定理」が成り立つことを確認する。ちょっと粗雑だが、これが通れば素数と考えることにしよう。
一応、大きな素数を見つけ出すVIができたようだが、問題は結果が正しいかどうか確認する方法がないことだ。すばらしい手抜きだと思ったブルーバックスの「素数の不思議」の１０万までの素数表に類するものが手元にない。今できる方法は、暗号プログラムを作り上げて上手く動くことを確認するのが良いだろう。
もうすぐ夏の休暇が始まるからゆっくり楽しむことにしよう。
See you! Nigel Yamaguchi 戻る