Chapter Twelve

第12話

今回は公開鍵N,e と秘密鍵dを決めるVIを作ろう。
その前に、繰り返しになるが手順をもう一度確認しておこう。
１）素数を二つ選ぶ。p, q とする。
２）N = p * q を計算する。
３）(p-1) と(q-1) の最小公倍数L を求める。
４）L と互いに素となるe を選ぶ。
５）1 = L*c + e*d となるd を求める。
計算の途中で、"mod N"と"mod N"の積が出てくるので、最大U32でVIを作ろうとしたとき、NはU16の数にとどめないといけない。従ってp, qはU8の数字になる。
暗号化、復号化にフェルマーの定理を使っている関係からNは平文をブロック化したときの数値よりも大きい必要がある。フェルマーの定理については、次回ぐらいにふれることになると思う。本格的な暗号VIを作るときには同じ考え方で変数のサイズを決定する。
Nがあまり小さな数になっても困るので、128から255の間の素数からp, qを選ぶことにしよう。条件に合うものを列挙すると次の23個になる。
131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,
211,223,227,229,233,239,241,251
本来は素数を探すことも重要なポイントだが、ここでは手順１、２を軽くクリアしたとして先に進もう。
最小公倍数は積を最大公約数で割ることによって得られる。
最大公約数を求めるには、ユークリッドの互除法を使う。ふつうの人は名前ぐらいしか覚えていないと思うが、割算の余りで除数を割るという計算を割り切れるまで繰り返し、最後の除数が、最大公約数となる、という計算方法だ。最大公約数が１のときそれらの数の関係を"互いに素"という。

これで手順３がクリアできる。
手順４は"L と互いに素となるe "を見つけるのだが、適当な数から順番にGCM＝１となるまで探していけばよい。
問題は、手順５だ。
L とe が"互いに素"のとき1 = L*c + e*d となる整数d, cが存在する。
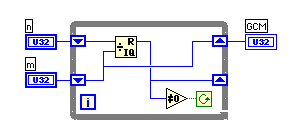
手順が少しややこしいのだが、互除法の副産物としてdを求めることができる。互除法では余りを使うが、その時に出てくる商をKiとしてXiを計算していき、余りが１になったときのXiがd である。

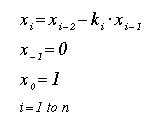
マイナスがでてくるのが困るのだが、しょうがないので符号付きU32(?)の引き算を作ってしまった。分かりにくいがダイアグラムと式を比べれば、手順は理解できると思う。


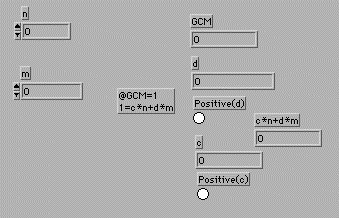
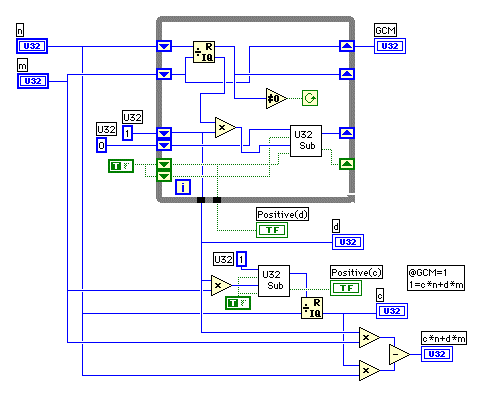
結果として得られるd はL, e の組み合わせによって正の場合もあれば、負の場合もある。d が負の場合は、解読の時の計算ができない（と思う）ので、e を選ぶときにd が正になるものを選ぶことにした。
これで全ての手順が用意できた。p, q を入力するとN, e, d を出力するVIが下のダイアグラムだ。


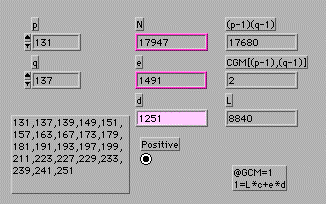
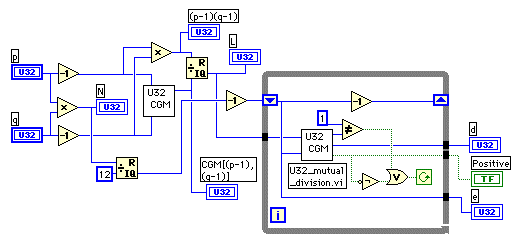
上のダイアグラムでGCMを求めるアイコンがU32 CGMとなっているのをいま気がついたが、まあ、いいでしょう。
今回は少し長くなってしまった。
See you! Nigel Yamaguchi 戻る