更新履歴
7. Warren & Bodensteinの散乱強度式を用いた炭素の二次元解析法
―結晶子サイズ分布解析―
7.1 原理
第2章では、Diamondの方法が、炭素網面による散乱強度がDebyeの散乱強度の式に従うとして、 結晶子サイズが既知の数種類のモデル炭素の11バンドの理論散乱強度を求め、 被測定炭素試料の結晶子サイズをこれらの理論散乱強度でフィッティングを行い、解析する方法であることを紹介した。また、この方法では、単一網面からの理論散乱強度のみの計算しかなされておらず、 積層網面部による00l回折線強度およびhk0回折線の変調等が考慮されていないことなどから、 厳密には単一網面から構成される試料にしか適用できず、積層網面体群を含む系には適用できないことも指摘した。 さらに、Warren & Bodensteinらが、Diamondの散乱強度式を拡張し、積層網面体群を含む系に適用できる理論散乱強度式を提案したことも第6章で述べた。
Fujimoto & Shiraishiは、Diamondの方法におけるDebyeの散乱強度式をWarren & Bordesteinの散乱強度式で置き換えると、 11バンドのみならず回折パターン全体にわたってフィッティングが行えるため、a, b軸方向の結晶子サイズ分布のみならず、c軸方向の結晶子サイズ分布も同時に求められることになり、二次元的に炭素の構造解析が可能となると考えた[1,2]。 彼らの方法は、Warren & Bodensteinの理論散乱強度式を用いて10000種類以上のモデル炭素結晶子について理論散乱強度を計算し、 それらを基に最小二乗法により実測X線回折パターンをフィッティングし、LaおよびLcサイズの分布を二次元的に解析するというものである。この方法によって得られる結果はおよそFig.7.1のようになる。
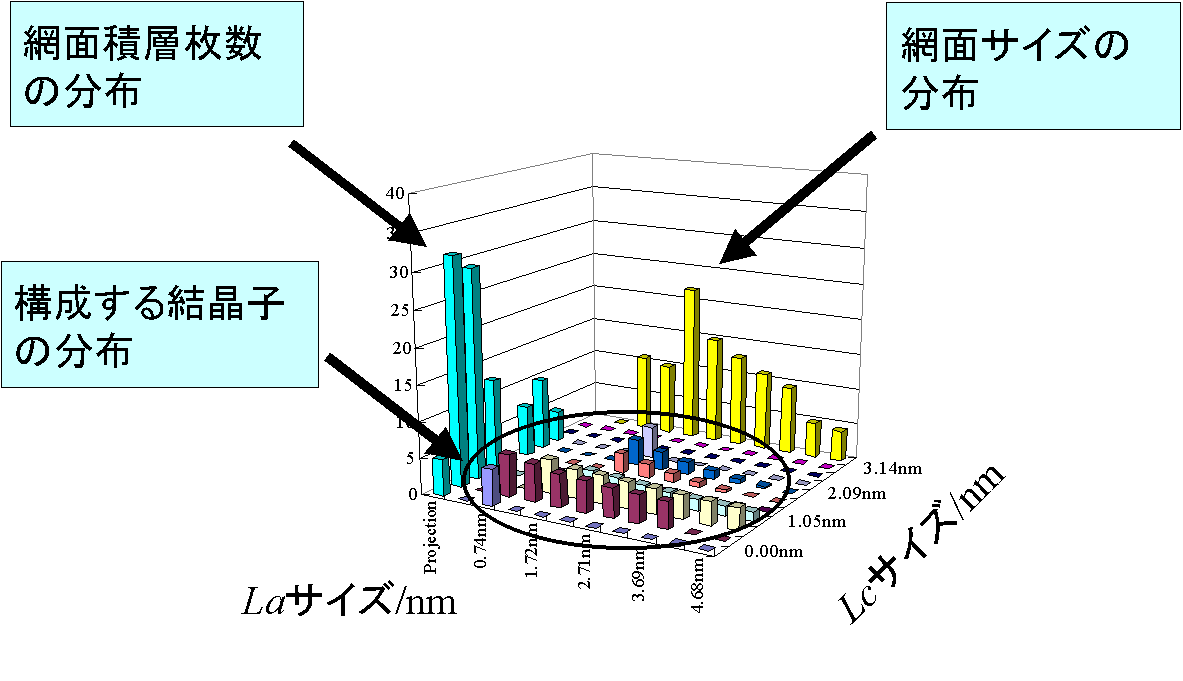
Fig.7.1 二次元解析法によって得られる結晶子サイズ分布結果イメージ
7.2 解析対象試料
第6章でも述べたように、Warren & Bodensteinの理論散乱強度式は乱層構造性炭素に関する散乱強度式であるため、 黒鉛化の進んだ材料、すなわちABAB型積層構造をとるような材料に対しては適用できない。易黒鉛化性炭素材料の場合、 およそ1500℃以下で炭素化された炭素材料が解析対象となる。また選択配向の強い試料に関しては、 フィッティングが困難となるため、実測強度の測定に工夫が必要となる。 難黒鉛系材料の場合には、黒鉛系材料ほどの配慮なく解析が可能である。
7.3 解析データ例
実測散乱強度を結晶子サイズが既知の10000種類以上のモデル結晶子の組み合わせによってフィッティングを行うため、 Fig.7.2およびFig.7.3に示すようなフィッティング結果と二次元的なヒストグラムが得られる。 このグラフは1400℃で焼成したメソカーボンマイクロビーズの解析例である[1]。 すなわちLaサイズおよびLcサイズを軸にとるとすべてのLa およびLcサイズの組み合わせに相当する結晶子の存在割合がヒストグラムとしてプロットされる。
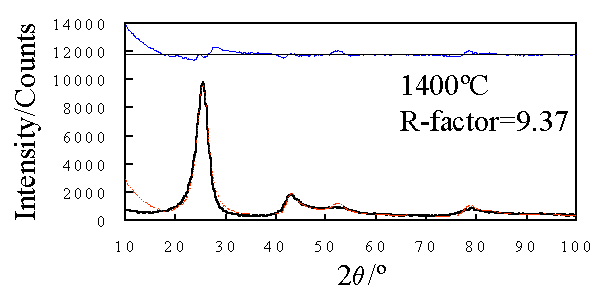
Fig. 7.2 実測X線回折強度のフィッティング結果
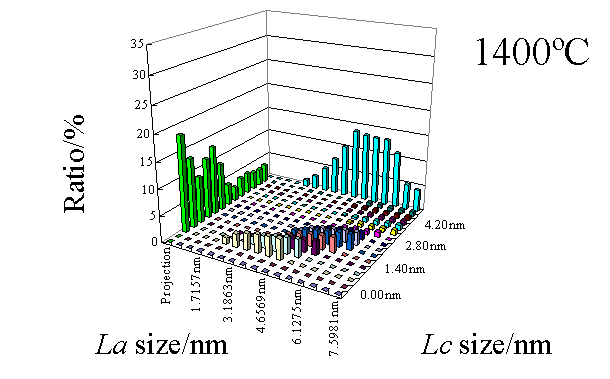
Fig. 7.3 二次元解析結果
7.4 解析手順
二次元解析法の手順は、基本的にDiamondの方法と同じである。
(1)未知試料中に存在すると予想されるモデル網面の想定
(2)想定したモデル網面からの理論散乱強度の計算
(3)未知試料の強度測定
(4)求めた実測強度の理論散乱強度による最小二乗フィッティング
(5)各理論散乱強度の重みからのモデル網面の重量分率および平均結晶子サイズの算出
の5つのステップからなる。Diamond法との違いはフィッティング範囲が11バンドだけではなく、回折パターン全体であることである。
参考文献
[1] 藤本宏之、白石稔、第26回炭素材料学会年会予稿集、356-359(1999)
[2] Hiroyuki Fujimoto, Minoru Shiraishi, Carbon 39, 1753-1761(2001)