本ホームページに記載されている内容を論文等に引用される場合には、 参考文献として本ホームページの制作者　藤本宏之およびアドレスを掲載してください。 更新履歴 2016/09/23（金）　ホームページ全体の見直し 2011/06/16（木）　アクセスカウンター設置 2011/06/05（日）　文章体裁見直し 2001/08/19（日）　掲載開始日 6. Warren & Bodensteinの方法 6.1 原理 　Diamondの方法(2.章参照）は、炭素網面による散乱強度がDebyeの散乱強度の式に従うものとして､ 結晶子サイズが既知の数種類のモデル炭素の11バンドの理論散乱強度を求め、 被測定炭素試料の結晶子サイズをこれらの理論散乱強度でフィッティングを行い、 解析する方法であることはすでに述べた。しかしながら､Diamondの方法では､ 単一網面からの散乱強度のみの計算しかなされておらず､積層網面部による00l回折線強度 およびhk0回折線の変調等が考慮されていないことなどから､ 厳密には単一網面から構成される試料にしか適用できず、積層網面体群を含む系には適用できない。 こうした理由からWarren & Bodensteinは､Debyeの散乱強度式を拡張し、 積層網面体群を含む系に適用できる理論散乱強度式を提案した[1] 。すなわち彼らは､積層網面体群からの干渉性散乱強度Ieu を炭素網面の積層枚数Mおよび単一網面内の炭素原子の数Nを用いて 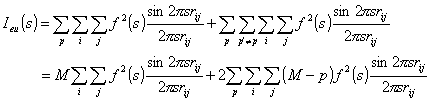(）　(6.1) で表わした。ここで、2q,l, fは、 それぞれ回折角、Ｘ線波長、原子散乱因子である。またrijは２つの炭素原子間距離である。 iおよびjに関する総和は、単一網面内における2つの原子間の干渉性散乱を表し、 pに関する総和は異なる網面間における2つの原子間の干渉性散乱を表している。 Warren & Bodensteinは円盤状の結晶子を考え､2枚の炭素網面の相対的な幾何学的な位置関係を考慮し 第2項をFourier積分で近似的に置き換え、１原子あたりの干渉性散乱Icohを以下のように誘導した｡ 　　　　　　　　　　 　(6.2) 　　　　　　 　　　　 　　　 　　　(6.3) 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(6.4) 本方法は、この式を用いて、理論散乱強度を計算し実測強度との比較を行うことによって、 未知試料の構造について、解析を行うものである。 彼らは比較的小さな結晶子サイズのカーボンブラックについて その散乱強度の計算を行い、その有効性を検討している。 また本方法では、未知試料中の全炭素原子のうち、炭素網面を構成する原子の割合が次式で得られる。 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(6.5) A1:100-004回折線間(2q=40-60°)におけるベースラインより上の部分の面積 A2: 100-004回折線間におけるベースラインより下の部分の面積 A3: 2q=40-60° における単体炭素原子からの干渉性散乱曲線より下の部分の面積 a:A1のA2に対する比 6.2 解析対象試料 　この方法において、Warren & Bodensteinは、式（6.1）の第2項を計算するために, 2枚の炭素網面に関して幾何学的解析を行い、Fourier近似積分を行っている。近似積分の物理的な意味を考慮すると最終的に誘導された理論散乱強度式は、 乱層構造炭素に関する理論散乱強度式と解釈される。したがって、この方法は黒鉛化処理を施した、いわゆるABAB型積層秩序性を有するような炭素材料の解析には適用できない。 6.3 解析データ例 　 Fig.6.1は本方法で解析を行った場合に得られる結果の一例である。 実測散乱強度から得られる平均結晶子サイズおよび格子定数を用いて理論散乱強度を計算し 重ね合わせるとおよそのプロファイル形状が一致することがわかる。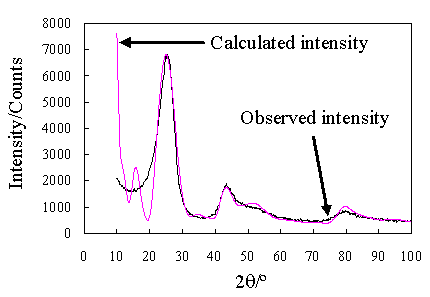 Fig.6.1 Warren & Bodensteinの方法による解析例 6.4 解析手順 　解析手順は、以下の通りである。 (1) 未知試料のＸ線回折パターンの測定 (2) 未知試料の回折線からの結晶子サイズLaおよびLcの算出 (3) 得られた結晶子サイズに相当する理論散乱強度の計算 (4) 実測散乱曲線と理論散乱曲線の比較 (5) 炭素網面を構成する炭素原子の割合の算出 参考文献 [1] B.E.Warren and P.Bodenstein, Acta Cryst., 18(1965)282-286 [2] Hiroyuki Fujimoto and Minoru Shiraishi, Carbon, 39, 1753-1761(2001) [3] Hiroyuki Fujimoto, Carbon 41, 1585-1592(2003)