本ホームページに記載されている内容を論文等に引用される場合には、
参考文献として本ホームページの制作者 藤本宏之およびアドレスを掲載してください。

更新履歴
5. Debyeの理論散乱強度式
5.1 原理
X線による散乱には干渉性散乱と非干渉性散乱があり、前者はDebyeの理論散乱強度式によって計算することができる。
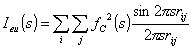
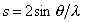 (5.1)
ここで、f, rij
はそれぞれ原子散乱因子、2つの原子iおよびj間の原子間ベクトルのスカラー量(原子間距離)である。
Diamondは、数種類のモデル網面(Diamondの方法Fig.3.5.1参照)について原子1個あたりの理論散乱強度を計算するために上式を以下の式に変形表現している。 (5.1)
ここで、f, rij
はそれぞれ原子散乱因子、2つの原子iおよびj間の原子間ベクトルのスカラー量(原子間距離)である。
Diamondは、数種類のモデル網面(Diamondの方法Fig.3.5.1参照)について原子1個あたりの理論散乱強度を計算するために上式を以下の式に変形表現している。
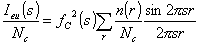 (5.2)
ここで、n(r)は網面中に存在する炭素原子間ベクトルrの数である。
この式を用いてモデル網面の理論散乱強度の計算を行うためには、Nc, n(r)およびrを あらかじめ求めておく必要がある。
これが案外と面倒な作業となる。筆者はFig.5.1に示した網面モデルを提案し計算を行っている[1]。 これらのモデル網面は一定の規則の下に考案されたモデルであるため、
すべてのパラメータがn の関数として表現できる。
それ故、コンピュータを用いた理論散乱強度計算プログラムの記述も極めて容易になる。 (5.2)
ここで、n(r)は網面中に存在する炭素原子間ベクトルrの数である。
この式を用いてモデル網面の理論散乱強度の計算を行うためには、Nc, n(r)およびrを あらかじめ求めておく必要がある。
これが案外と面倒な作業となる。筆者はFig.5.1に示した網面モデルを提案し計算を行っている[1]。 これらのモデル網面は一定の規則の下に考案されたモデルであるため、
すべてのパラメータがn の関数として表現できる。
それ故、コンピュータを用いた理論散乱強度計算プログラムの記述も極めて容易になる。
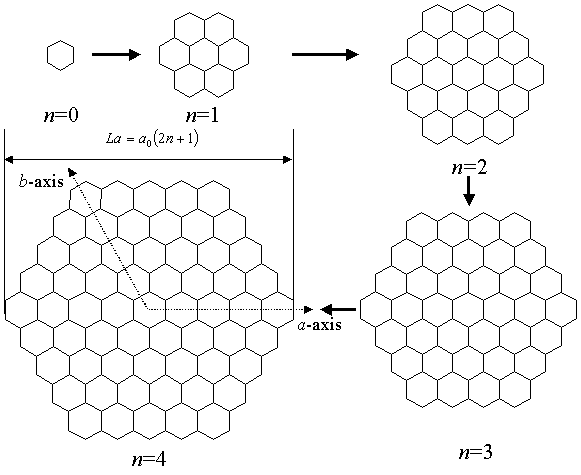
Fig.5.1 筆者が提案したモデル網面
5.2 計算上の注意点と計算結果の一例
Debyeの散乱強度式をそのまま解釈すると互いに異なる2つの炭素原子間の干渉性散乱の和となっているが、
実際にはそれぞれの炭素原子自身からの干渉性散乱をも加味する必要がある。
炭素原子自身からの干渉性散乱を加味しなければ、ある散乱角度範囲で理論散乱強度が負になり、注意が必要である。
厳密には、Debyeの散乱強度式は、式(5.1)は正確ではなく、次式のように書くべきである。
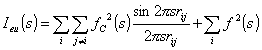 (5.3)
あるいは炭素原子1個あたりの強度で表現するとすれば (5.3)
あるいは炭素原子1個あたりの強度で表現するとすれば
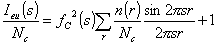 (5.4)
Fig.5.1におけるn=4の時のモデル網面の理論散乱強度を上式によって計算した結果を Diamondが求めた理論散乱強度(Diamondの方法の項のFig.2.1参照、La=2nm)と比較した結果をFig.5.2に示す。
両者のモデル網面形状は異なっているが、理論散乱強度曲線は、ほぼ一致していることがわかる。
この結果が示唆することは、炭素数がおよそ等しければ、網面形状が多少異なっていても散乱強度はほとんど同じになるということである。
したがって、未知試料中に含まれる網面を厳密に決めることに重点を置くよりも、
平均的な網面としてどのような網面が含まれるのかといった観点から網面を選定する方が良いことを示している。 (5.4)
Fig.5.1におけるn=4の時のモデル網面の理論散乱強度を上式によって計算した結果を Diamondが求めた理論散乱強度(Diamondの方法の項のFig.2.1参照、La=2nm)と比較した結果をFig.5.2に示す。
両者のモデル網面形状は異なっているが、理論散乱強度曲線は、ほぼ一致していることがわかる。
この結果が示唆することは、炭素数がおよそ等しければ、網面形状が多少異なっていても散乱強度はほとんど同じになるということである。
したがって、未知試料中に含まれる網面を厳密に決めることに重点を置くよりも、
平均的な網面としてどのような網面が含まれるのかといった観点から網面を選定する方が良いことを示している。
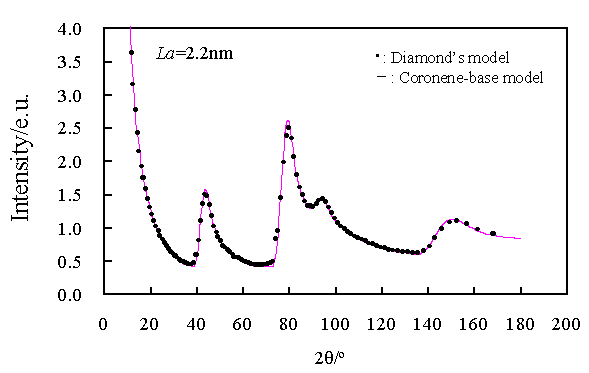
Fig.5.2 理論散乱強度計算結果の一例
(5.4)式より得られる強度は干渉性散乱項のみである。ところが実測散乱強度には、非干渉性散乱、偏光因子、吸収因子などが影響を与える。
したがって、実際の理論散乱強度を求めるためには、(5.4)式を以下の式に代入する必要がある。
 (5.5)
非干渉性散乱強度は、Hajduの非干渉性散乱式[2,3]にRulandの減衰関数Q(s/2)[4]を乗じたものを採用すると良い。 (5.5)
非干渉性散乱強度は、Hajduの非干渉性散乱式[2,3]にRulandの減衰関数Q(s/2)[4]を乗じたものを採用すると良い。
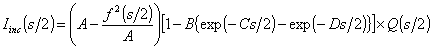 (5.6) (5.6)
A=6, B=0.4972, C=1.8438, D=7.8917
参考文献
[1] 藤本宏之、白石稔、炭素 No.187, (1999)83-87
[2] F.Hajdu, Acta. Cryst., A27(1971)73-74.
[3] F.Hajdu, Acta. Cryst., A28(1972)250-252.
[4] W.Ruland, Britt. J. Appl.Phys., 15(1964)1301-1307.
|

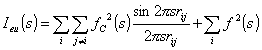 (5.3)
(5.3)
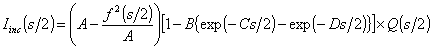 (5.6)
(5.6)