本ホームページに記載されている内容を論文等に引用される場合には、 参考文献として本ホームページの制作者　藤本宏之およびアドレスを掲載してください。 更新履歴 2016/09/23（金）　ホームページ全体の見直し 2011/06/05（日）　内容修正 2001/08/19（日）　掲載開始日 3. Hirschの方法 3.1 原理 　この方法は、石炭やピッチのような比較的網面サイズの小さな試料中の炭素網面の平均積層枚数および積層分布を 評価するためにHirschによって、1954年に提案された方法である[1]。彼は、002バンドおよび20Aバンドを含む 回折角度領域における散乱強度を定量的に扱うために、一次元のFourier変換 　　（ただし、s=2sinq/ l） 　　  (3.1) を考え計算を行った。層内の構造が均一であると仮定すると、(3.1)式のFourier解析結果は、 任意の層面からそれに平行に存在する層面の分布を与えることになる。Fig.3.1はFourier変換結果の一例であるが、関数P(u)はある任意の層面から距離uの点における平行な層面の存在確率を意味している。 従って、P(u)は炭素層面間隔距離の整数倍に等しい点において極大値をとり、 極大値の中間の距離の時には極小値をとることになる。また、P(u)は一般に振動関数となり、 振幅が減衰していくことは距離uが長くなるにつれて、平行な網面の存在確率が小さくなることを示している。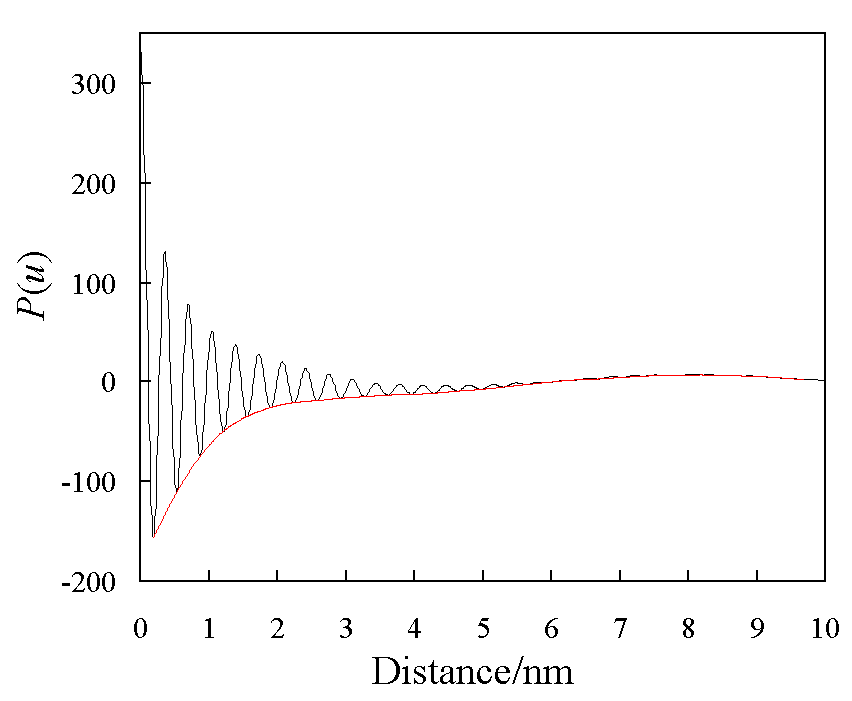 Fig.3.1 Fourier解析の一例 　彼は、このFourier変換の物理的意味合いを以下のように説明している。選択配向した積層構造を持つ試料において、c軸に投影される電子密度関数t(x)を考えると、 この関数はxが炭素層面間隔距離の倍数に等しくなる点においてピークを持つ。もし、P(u) が完全に選択配向した試料からの実測散乱強度のFourier変換であるなら、P(u)はすべての点x にわたって平均化された点xおよびx+uにおける密度の積に等しくなるはずである。 すなわち 　　　　　　　　　　　　　　　　　　　　(3.2) となり、原子間ベクトルに対応するところにピークが現れることになる。 3.2 原理の拡張 　Hirschの方法によって求められる振動関数の極小値を結んで得られる包絡線と振動関数によって囲まれる部分の面積から 網面の積層分布を得ることができる。白石によって報告された方法を以下に紹介する[2]。 すべての層面が、同じ面積で等間隔に積層しているものとすると、P(u)=0におけるピークはその層面自身を表しており、 次のピーク（第１ピーク）は２層目、その次のピーク（第２ピーク）は３層目に由来するピークとなる。 P(u)のm番目のピークの面積p(m)は 　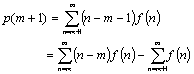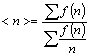　　　　　　　　　　　　　　　　　(3.3) となる。f(n)はn層を含む積層構造の重量割合である。 それ故 　　　　　　　　　　　　　　　　(3.4) 従って 　　　　　　　　　　　　(3.5) となる。p(m)はP(u)の１番目のピーク以上のピークで求めることができる。従って、m≧2 のf(m)が得られる。２層以上を含む積層構造の全体に対する割合で規格化すると 　　　　　　　　(3.6) と表わすことができる。 　層面の積み重なりの数の平均値<n>は以下の式より算出される。 　　　　　　　　　　　　　　　　　　　　　　(3.7) 3.3 解析対象試料 　これまで、石炭をはじめとして、比較的低温で焼成された炭素材料に関する解析例が多数存在する[2-8]。 また、本解析方法は、均一な層内構造の仮定の下に分布を求めるものであるため、 多相系炭素の場合には、非常に精度良く002回折線が分離されない限り適用が困難である。 3.4 解析手順 　Hirschの提案した解析方法の手順は、基本的に (1)未知試料の002回折線強度の測定 (2)測定回折線強度の強度補正 (3)補正回折線強度のFourier変換によるPatterson関数計算 (4)求めたPatterson関数の逆Fourier変換による計算結果の信頼性確認 (5)網面の積層分布の算出 の５つのステップからなる。 3.5 解析結果の一例と解釈上の注意点 　Fig.3.2にFourier解析結果より得られる積層分布解析結果の一例を示す。13層目でヒストグラムが負になっていることがわかるが、 これはFig.3.1のFourier曲線がFourierリップルの影響を受けているからである。 従ってヒストグラムで信頼性のあるのは最大でも12層目までと解釈される。 Fourierリップルは、測定時のサンプリング間隔やS/N比などの影響により変化するので注意が必要である。 こうした議論は文献[8,9]において詳しくなされている。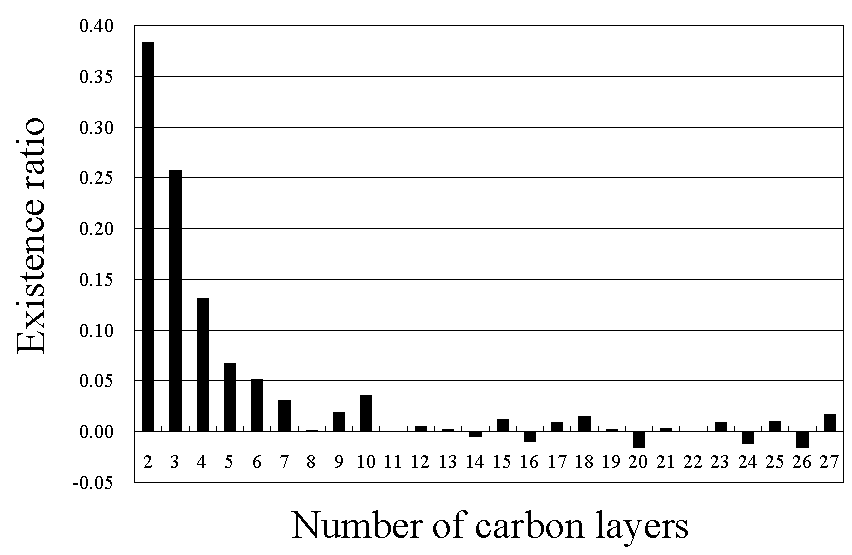 　 Fig.3.2 Fourier解析結果より得られる積層分布解析結果 参考文献 [1] P.B.Hirsch, Proc.Roy.Soc.,A226(1954)143-169 [2] W.Ruland, Carbon, 2,365-370(1965) [3] M.Shiraishi,K.Kobayashi,Bull.Chem.Soc.Jap., 46(1973)2575-2578 [4] 白石稔, 真田雄三, 日本化学会誌, 1(1976)153-160 [5] 横野哲朗, 渋谷隆夫, 真田雄三, 日本化学会誌, 8(1978)1132-1136 [6] 小川一太郎, 小林和夫, 炭素 No.120(1985)28-33 [7] 井本浩, 小丸篤雄, 東秀人, 日本国公開特許, 特開平6-89721(1994) [8] 藤本宏之, 白石稔, 炭素 No.167, 101-107(1995) [9] 藤本宏之、白石稔 炭素 No.213, 144-150(2004)