更新履歴
2. Diamondの方法
2.1 原理
この方法は、石炭やピッチのような比較的網面サイズの小さな試料中の炭素網面の平均サイズ及びその分布を評価するために Diamondによって1956年に提案された方法である[1-4]。構造が未知の炭素試料は、構造が既知の数種類のモデル炭素網面(Fig.2.1) の集合体であるとの仮定の下に、未知試料のX線回折プロファイルにおける11バンドの実測強度Iosをモデル 網面の理論X線散乱強度Bi(s)に重量分率wiを乗じたものの和で表現し、 最小二乗法によって各々の重量分率を求め、網面サイズの分布を評価する方法である。すなわち、誤差をv(s)とすると
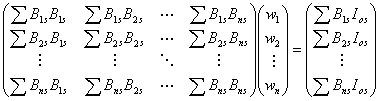 (2.5)
(2.5)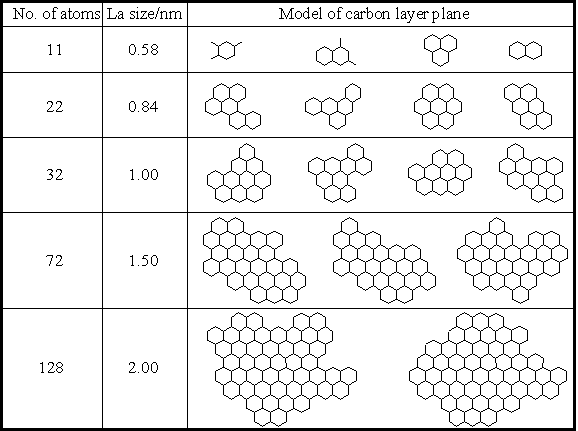
Fig.2.1 Diamondが採用したモデル網面
2.2 解析対象試料
本解析方法では、ヘテロ原子を含まない単一網面モデルからの理論散乱強度に基づいて、実測散乱強度をフィッティングしているため、 網面の積層枚数が比較的小さく、ヘテロ原子などの異種原子があまり含まれていない炭素材料が理想的な解析対象となる。 網面サイズが大きくなっても、単一網面からの理論散乱強度が計算できる限り、解析は可能であるが、 実際の試料においては網面サイズが大きくなるとVon der Waals力による網面の積層が生じるため次第に誤差が大きくなる。 こうした理由から、経験的には積層枚数は4-6層程度が限界かもしれない。 また、石炭やピッチあるいは低温で焼成された炭素は、一般にジグザグ網面から形成されているため、 本方法により得られる炭素網面サイズは透過型電子顕微鏡観察によって得られる網面サイズに比べて、小さくなる[9]。
2.3 解析手順
Diamondの提案した解析方法の手順は、基本的に
(1)未知試料中に存在すると予想されるモデル網面の想定
(2)想定したモデル網面からの理論散乱強度の計算
(Debyeの理論散乱強度計算方法の項を参照)
(3)未知試料の11バンドの強度測定
(4)求めた実測強度の理論散乱強度による最小二乗フィッティング
(5)各理論散乱強度の重みからのモデル網面の重量分率および平均網面サイズの算出
の5つのステップからなる。
2.4 解析結果の一例と解釈上の注意点
以上に説明した手順で試料中の網面サイズ分布が得られることになる。以下に実際の解析例を紹介する。Fig.2.2は、同一のデータに対してコロネンベースモデル、ピレンベースモデルおよびコロネン・ピレン混合モデルを用いてフィッティングを行った例である。いずれの場合においても良好にフィッティングされており、平均網面サイズもほとんど変わらないが、Fig.2.3に示すように網面サイズ分布ヒストグラムではかなり違った結果となる。混合モデルでフィッティングを行った場合には、最大網面サイズが3.67nmとなっているが実際にはそれ以上の網面が存在しているために、ピレンベースモデル、コロネンベースモデルで計算した場合には、より大きな網面の存在を示唆するヒストグラムが得られている。網面サイズをあらかじめ予想できない場合には、それぞれのモデルで計算を行って、結果を比較する必要がある。
本解析法によって得られる網面サイズの分布および平均網面サイズは、一般に透過型電子顕微鏡観察から得られる網面サイズ分布とは一致しない。前者のデータの方が後者のデータよりも小さく見積もられる。これは網面が一般にジグザグ状に折れ曲がっていることによる。透過型顕微鏡ではジグザグ網面全体の大きさを反映したサイズが見積もられるが、X線回折プロファイルにおける11バンドは面内反射であるため、ジグザグ状網面中の折れ曲がり単位を構成するフラットな部位からの反射を反映するためである[8]。
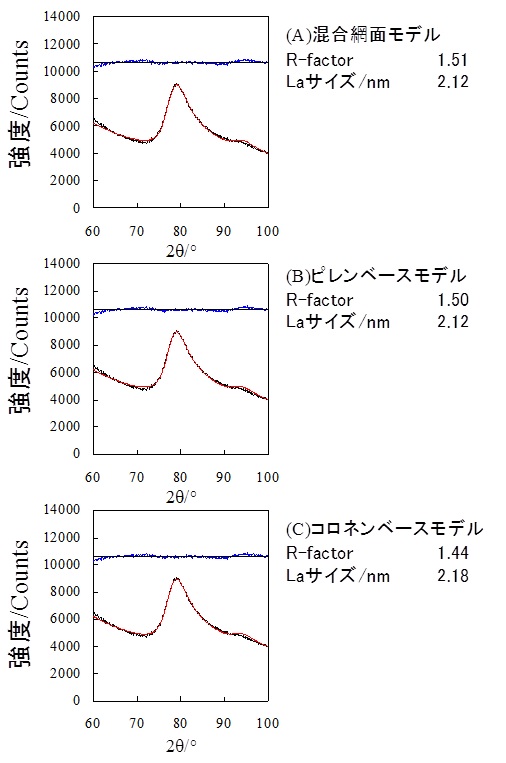
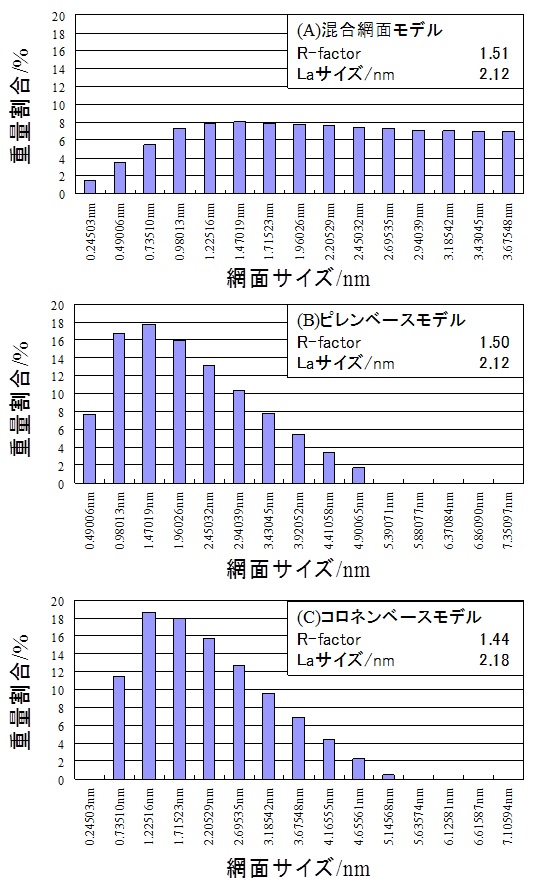
Fig.2.2 Diamond法によるフィッティング結果 Fig.2-3 網面サイズ分布結果
参考文献
[1] R.Diamond, Ph.D.Dissertation, University of Cambridge, England, 1956.
[2] R.Diamond, Acta. Cryst. 10(1957)359-363.
[3] R.Diamond, Acta. Cryst. 11(1958)129-138.
[4] R.Diamond, Phil. Trans. Roy. Soc. London A252(1960)193-223.
[5] J. D. Brooks and J. F. Stephens, Carbon 2(1965)379-384.
[6] 白石稔、小林和夫、日本化学会誌 6(1972)1135-1139.
[7] Minoru Shiraishi and Kazuo Kobayashi, Bull. Chem. Soc. Japan, 46(1973)2575-2578.
[8] 藤本宏之、白石稔、炭素、No.187(1999)83-87.
[9] 藤本宏之、第27回炭素材料学会年会予稿集3C03, (2000)366-367
[10] 藤本宏之、白石稔、炭素 No.213, 144-150(2004)