問題４-１-３ 解説

以下， \(\log_{10}\) と \(\log_e\) はそれぞれ \(\log\) と \(\ln\) と表記し， \(N(M)\) は \(N\) などと略記します．

（１） \(E\) の式， \(\log E = 4.8 + 1.5M\) と \(N\) の式， \(\log N = 9.0 - 1.0M\) を指数表示します． \begin{eqnarray*} E & = & 10^{4.8+1.5M} = e^{\ln10(4.8+1.5M)} = e^{4.8\ln10}\times e^{(1.5\ln10)M}, \\ N & = & 10^{9.0-1.0M} = e^{\ln 10(9.0-1.0M)} = e^{9.0\ln10}\times e^{(-1.0\ln10)M}. \end{eqnarray*} \(N\) を \(M\) で微分して絶対値を取ると， \[ \left|\frac{dN}{dM}\right| = 1.0\ln10\,e^{9.0\ln10}\times e^{(-1.0\ln10)M}. \] これに \(E\) を掛けて \(M_1\) から \(M_2\) まで積分すると， \begin{eqnarray*} E_T & = & \int_{M_1}^{M_2}E\left|\frac{dN}{dM}\right|dM, \\ & = & 1.0\ln10\,e^{13.8\ln10}\int_{M_1}^{M_2}e^{(0.5\ln10)M}, \\ & = & \frac{1.0\ln10}{0.5\ln10}e^{13.8\ln10}\left[e^{(0.5\ln10)M}\right]_{M_1}^{M_2}, \\ & = & 2\,e^{13.8\ln10}\left(e^{(0.5\ln10)M_2}-e^{(0.5\ln10)M_1}\right). \end{eqnarray*} \(M_1\) = 5， \(M_2\) = 8.5 とおいて， \[ E_T \approx 2.2\times10^{18}\ \mathrm{J}. \] これを 50 年で割って，地震のエネルギーの年平均値は， \[ 4.4\times10^{16}\ \mathrm{J/yr}, \] となります．地球全体での地震のエネルギーの年平均は水谷・渡部（1978）によると， 1920〜1976 年で 4.5\(\times\)10¹⁷ J/yr です．よって，上の計算結果は日本付近の地震のエネルギーが地球全体の約 10% を占めることを示します．

（２） 期間中最大の地震と東北地方太平洋沖地震の１回のエネルギーは次の通りです． \begin{eqnarray*} M_W=8.5：\ & & 10^{4.8+1.5\times 8.5} = 10^{17.55} \approx 3.5\times 10^{17}\ \mathrm{J}, \\ M_W=9.1：\ & & 10^{4.8+1.5\times 9.1} = 10^{18.45} \approx 2.8\times 10^{18}\ \mathrm{J}. \end{eqnarray*} これより \(M_W\) = 8.5 の地震の放出したエネルギーは日本付近の 50 年間の地震のエネルギーの約 16% を占めていることが分かります．そして \(M_W\) = 9.1 の東北地方太平洋沖地震については， 50 年分の地震のエネルギーのおよそ 1.3 倍ものエネルギーを放出したことになります．

(1) の別解

\(n\) と \(E\) の式から計算します．問題４-１-２（２）で導いた \(A\)， \(a\)， \(b\) の関係， \[ A = a - \log_{10}(b\ln 10), \] より \(a\) を求めると次の \(n\) の式を得ます． \[ \log n = 9.36 - 1.0M. \] よって， \(n\) と \(E\) の指数表示は次の通りです． \begin{eqnarray*} n & = & e^{\ln10(9.36-1.0M)} = e^{9.36\ln10}\times e^{(-1.0\ln10)M}, \\ E & = & e^{\ln10(4.8+1.5M)} = e^{4.8\ln10}\times e^{(1.5\ln10)M}. \end{eqnarray*} 地震のエネルギーの総量 \(E_T\) は \(EndM\) を \(M_1\) から \(M_2\) まで積分して， \begin{eqnarray*} E_T & = & \int_{M_1}^{M_2}E\,n\,dM, \\ & = & e^{14.16\ln10}\int_{M_1}^{M_2}e^{(0.5\ln10)M}dM, \\ & = & \frac{e^{14.16\ln10}}{0.5\ln10}\left(e^{(0.5\ln10)M_2}-e^{(0.5\ln10)M_1}\right). \end{eqnarray*} \(M_1\) = 5， \(M_2\) = 8.5 とおいて， \[ E_T \approx 2.2\times10^{18}\ \mathrm{J}. \]

補足：

この演習問題の計算過程から分かるように，地震の積算エネルギー \(E_T\) の見積もりは積分範囲の \(M_2\) = 8.5 で決まり， \(M_1\) = 5 の寄与はほとんどありません．そのため，問題では \(\log N\) を１本の直線で近似しましたが， \(M\) ≥ 7 の近似が正確ではないために，見積もった \(E_T\) はかなり大きな値となりました．下図のように \(\log N\) を２本の直線で近似すると正確さは多少向上すると思われます．この場合， \(E_T\) は約 1.6\(\times\)10¹⁸ J とかなり小さい値になります．

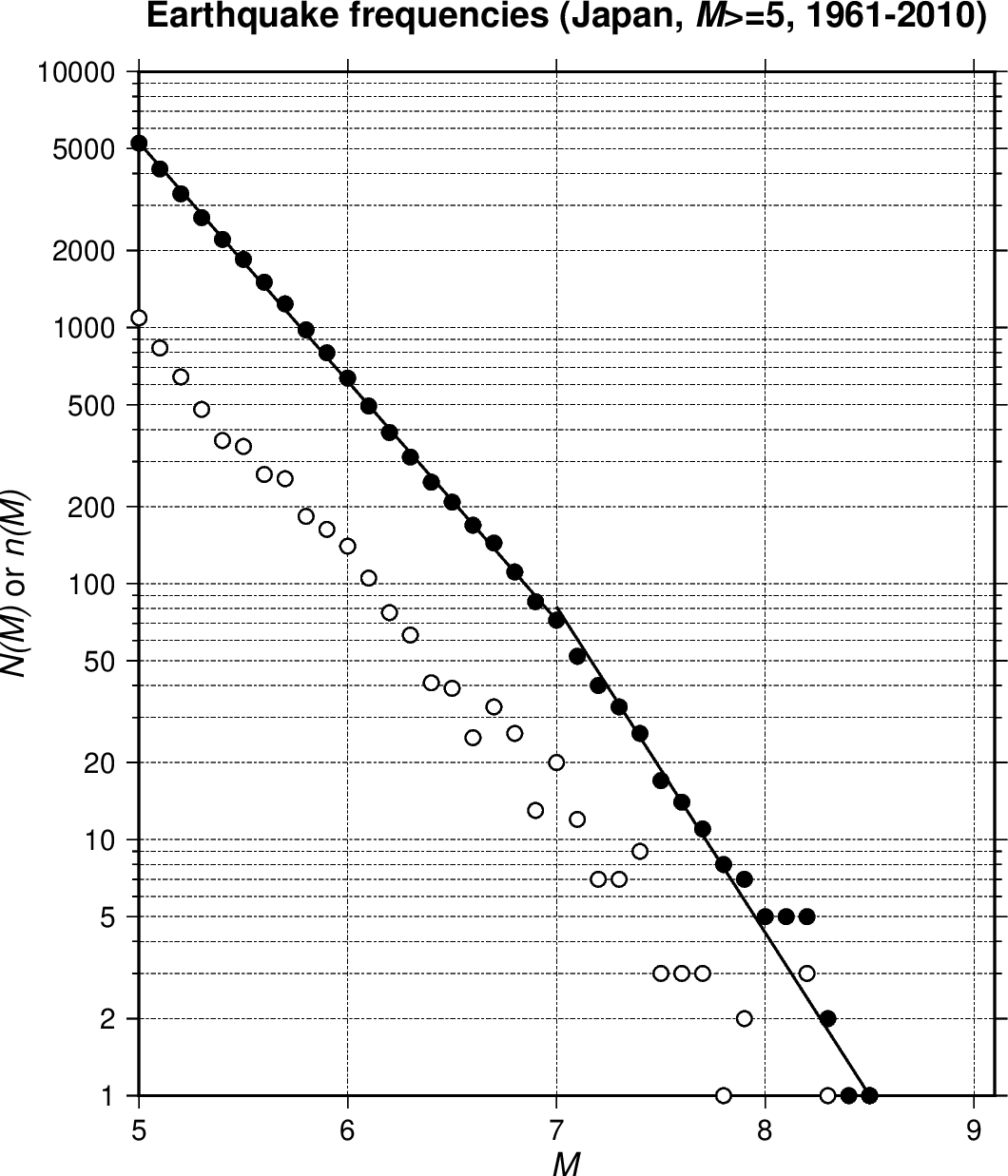
どちらにしろ，地震のエネルギーと発生頻度の式は経験式ですので，あまり詳細な議論は必要ないと思われます．それよりも，より正確な地震のエネルギーを見積もるためには，地震を種類に分けて（プレート間かプレート内か，浅発地震か深発地震か，など）解析することが考えられます．また，個々の地震の断層モデルから地震モーメントを求めエネルギーに換算するなどの高度な作業も必要と思われます．

参考文献：

• 水谷仁・渡部輝彦，第４章 地球熱学 (p.169-223)，岩波講座 地球科学１ 地球， 318 pp.，岩波書店，東京， 1978．

→ ホーム