問題7-3-4 解説
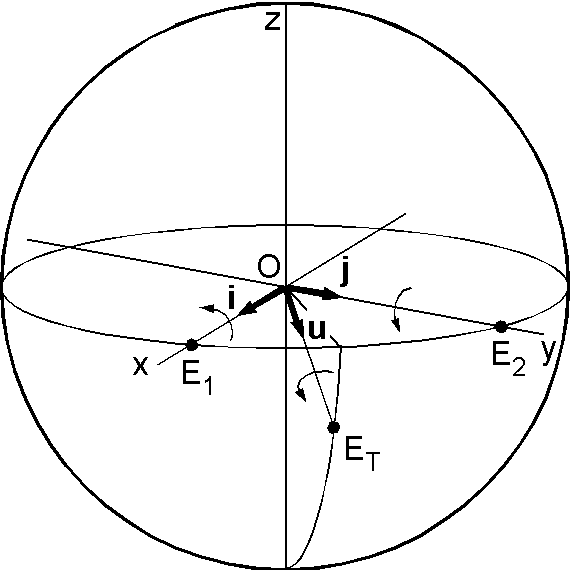
本文に示したように, x 軸と y 軸の回りの回転行列は次の通りです. \[ A_x = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{array}\right), \quad A_y = \left(\begin{array}{ccc} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{array}\right). \]
(1) 回転行列 \(A_1\) と \(A_2\) はそれぞれ上式の \(A_x\) と \(A_y\) で \(\theta\) = 90° として次のようになります. \[ A_1 = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right), \quad A_2 = \left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{array}\right). \] 全回転 \(A_T=A_2A_1\) は次のようになります. \begin{eqnarray*} A_T = \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right) & = & \left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{array}\right) \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right), \\ & = & \left(\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & -1 \\ -1 & 0 & 0 \end{array}\right). \end{eqnarray*}
(2) 以下の計算は,→ 回転行列に対応するオイラー極の求め方の式 (8), (10), (11) を使用します. \[ a_{32}-a_{23} = 1, \quad a_{13}-a_{31} = 1, \quad a_{21}-a_{12} = -1, \quad a_{11}+a_{22}+a_{33} = 0. \] となるので,オイラー極の経度 \(\phi_E\) は, \[ \phi = \tan^{-1}\left(\frac{a_{13}-a_{31}}{a_{32}-a_{23}}\right) = \tan^{-1}\left(\frac{1}{1}\right) = 45°. \] 緯度 \(\lambda_E\) は, \begin{eqnarray*} \lambda & = & \sin^{-1}\left(\frac{a_{21}-a_{12}}{\sqrt{(a_{32}-a_{23})^2 + (a_{13}-a_{31})^2 + (a_{21}-a_{12})^2}}\right), \\ & = & \sin^{-1}\left(\frac{-1}{\sqrt{3}}\right) = -35.26°. \end{eqnarray*} 回転角 \(\theta\) は, \[ \theta = \cos^{-1}\left(\frac{a_{11}+a_{22}+a_{33}-1}{2}\right) = \cos^{-1}\left(\frac{-1}{2}\right) = 120°. \] 以上より,全回転のオイラー極の緯度・経度は (35.3°S, 45°E) で回転角は 120° となります.
因みに,回転行列の掛け算を逆にすると全回転のオイラー極は次のように北半球の赤道に対象な位置となり,回転角は同じ 120° です. \[ A_1A_2 = \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{array}\right) \left(\begin{array}{ccc} 0 & 0 & 1 \\ 0 & 1 & 0 \\ -1 & 0 & 0 \end{array}\right) = \left(\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right). \] \begin{eqnarray*} \phi & = & \tan^{-1}\left(\frac{a_{13}-a_{31}}{a_{32}-a_{23}}\right) = \tan^{-1}\left(\frac{1}{1}\right) = 45°, \\ \lambda & = & \sin^{-1}\left(\frac{a_{21}-a_{12}}{\sqrt{(a_{32}-a_{23})^2 + (a_{13}-a_{31})^2 + (a_{21}-a_{12})^2}}\right), \\ & = & \sin^{1}\left(\frac{1}{\sqrt{3}}\right) = 35.26°, \\ \theta & = & \cos^{-1}\left(\frac{a_{11}+a_{22}+a_{33}-1}{2}\right) = \cos^{-1}\left(\frac{-1}{2}\right) = 120°. \end{eqnarray*}