問題７-３-３ 解説

下図で，既知の変数は \(\theta_1\)， \(\theta_2\)， \(\phi_1\)， \(\phi_2\)， \(\beta_1\)， \(\beta_2\) で，決定すべき変数は \(\theta\) と \(\alpha\) です．

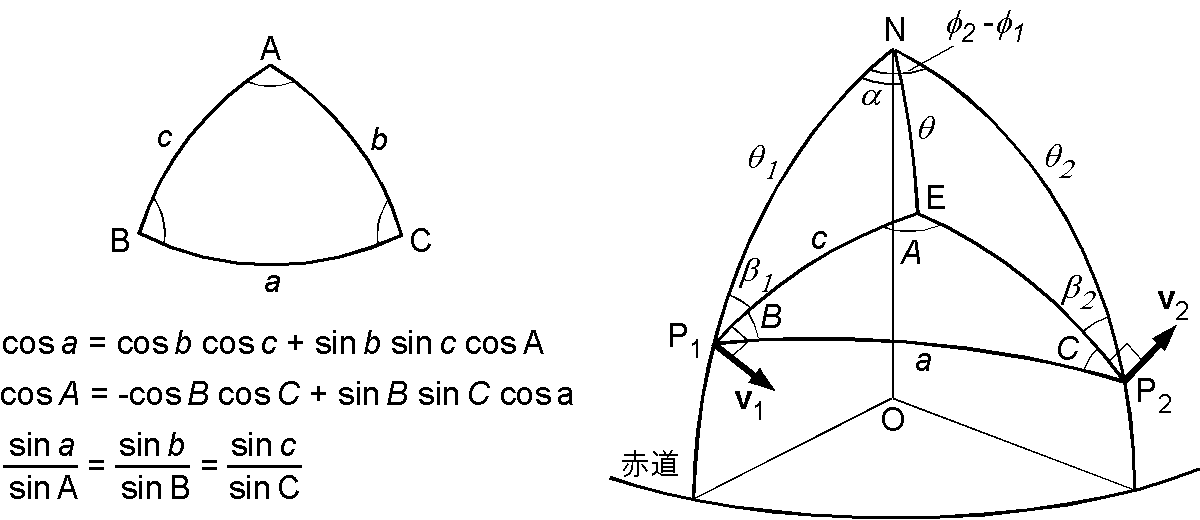
速度ベクトルに垂直な２本の大円の交点としてのオイラー極

（１）

  1. 三角形 NP1P2 で，１番目の余弦定理と正弦定理から， \begin{eqnarray*} \cos a & = & \cos\theta_2\cos\theta_1 + \sin\theta_2\sin\theta_1\cos(\phi_2-\phi_1), \\ \sin(\beta_1+B) & = & \sin\theta_2\sin(\phi_2-\phi_1)/\sin a, \\ \sin(\beta_2+C) & = & \sin\theta_1\sin(\phi_2-\phi_1)/\sin a, \end{eqnarray*} より \(a\)， \(B\)， \(C\) が決まります．
  2. 三角形 EP1P2 で２番目の余弦定理と正弦定理から， \begin{eqnarray*} \cos A & = & -\cos B\cos C + \sin B\sin C\cos a, \\ \sin c & = & \sin a\sin C/\sin A, \end{eqnarray*} より \(A\) と \(c\) が決まります．
  3. 三角形 NP1E で１番目の余弦定理と正弦定理から， \begin{eqnarray*} \cos\theta & = & \cos\theta_1\cos c + \sin\theta_1\sin c\cos\beta_1, \\ \sin\alpha & = & \sin c\sin\beta_1/\sin\theta, \end{eqnarray*} より \(\theta\) と \(\alpha\) が決まります．

最後に， \(\lambda_E\) と \(\phi_E\) を次式で決定します． \[ \lambda_E = 90 - \theta, \quad \phi_E = \phi_1 + \alpha. \]

（２） \(\theta_1\) = 50°， \(\theta_2\) = 60°， \(\beta_1\) = 30°， \(\beta_2\) = 20°， \(\phi_1\) = 90°， \(\phi_2\) = 160° を各式に代入し，途中結果は小数点以下２桁まで残すと，

  1.   \(a\) = 56.75°， \(B\) = 46.68°， \(C\) = 39.40°．
  2.   \(A\) = 106.08°， \(c\) = 33.53°．
  3.   \(\theta\) = 25.54°， \(\alpha\) = 39.84°．

以上よりオイラー極 \((\lambda_E, \phi_E)\) は (64.5°N， 129.8°E) となります．

→ ホーム