天体スケールの力学的エネルギー保存則
本文では,重力加速度が一定と見なせる地表付近での力学的エネルギー保存則, \[ \frac{1}{2}mv^2 + mgx = \frac{1}{2}mv_0^2 + mgx_0, \] を導きました.重力加速度が距離とともに変化する天体のスケールでも,同様の方法で,以下のように力学的エネルギー保存則を導くことができます.
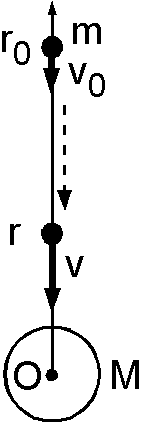
図のように,質量 \(M\) の天体の中心から r 軸を取り,質量 \(m\) の物体が r0 の位置から天体に向け落下する現象を考えます.物体は質点と見なし,天体の引力はその中心に位置する質量 \(M\) の質点の引力と同等とします.ニュートンの運動方程式と万有引力の法則から, \[ m\frac{d^2r}{dt^2} = -\frac{GMm}{r^2}. \] 両辺に \(dr/dt\) をかけて変形し, \(t_0\) から \(t\) まで積分すると, \begin{eqnarray*} m\frac{dr}{dt}\frac{d^2r}{dt^2} & = & -\frac{GMm}{r^2}\frac{dr}{dt}, \\ \frac{1}{2}m\frac{d}{dt}\left[\left(\frac{dr}{dt}\right)^2\right] & = & -\frac{GMm}{r^2}\frac{dr}{dt}, \\ \frac{1}{2}m\left[\left(\frac{dr}{dt}\right)^2\right]_{t_0}^t & = & -GMm\int_{t_0}^t \frac{1}{r^2}\frac{dr}{dt}dt. \end{eqnarray*} 時間 \(t_0 \rightarrow t\) で,物体の位置は \(r_0 \rightarrow r\),速度は \(v_0 \rightarrow v\) とすると, \begin{eqnarray*} \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2 & = & -GMm\left[-\frac{1}{r}\right]_{r_0}^r, \\ \frac{1}{2}mv^2 - \frac{1}{2}mv_0^2 & = & GMm\left(\frac{1}{r} - \frac{1}{r_0}\right), \\ \frac{1}{2}mv^2 - \frac{GMm}{r} & = & \frac{1}{2}mv_0^2 - \frac{GMm}{r_0}. \end{eqnarray*} となり,運動エネルギーと位置のエネルギーの和は一定となります.位置エネルギーの項に負記号が付いていて,地表付近の場合と異なる印象を与えますが,天体からの距離が大になるほど \(-GMm/r\) は大きくなるので(無限遠でゼロ),地表付近の場合と同じ理屈です.