問題1-1-3 解説
座標軸を下図のように取ります.
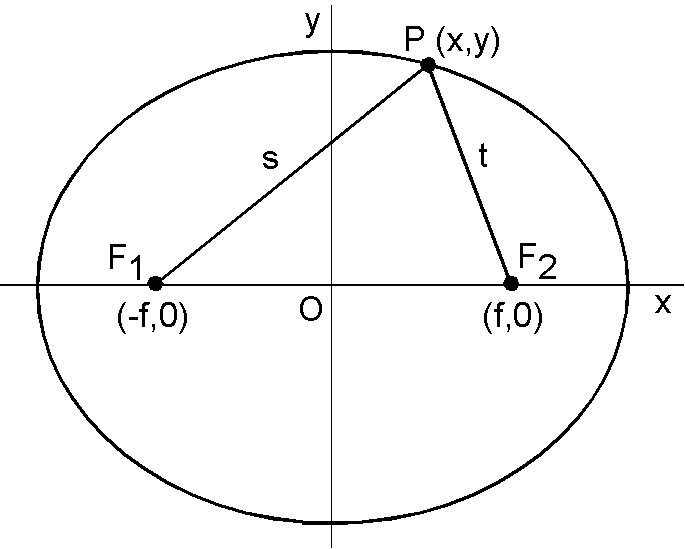
(1) 条件の \(s+t=2a\) より, \[ \sqrt{(x+f)^2 + y^2} + \sqrt{(x-f)^2 + y^2} = 2a. \] 計算を簡単にするために,左辺の第2項を右辺に移行してから2乗します. \begin{eqnarray*} \sqrt{(x+f)^2 + y^2} & = & 2a - \sqrt{(x-f)^2 + y^2}, \\ (x+f)^2 + y^2 & = & 4a^2 + (x-f)^2 + y^2 -4a\sqrt{(x-f)^2 + y^2}. \end{eqnarray*} 整理すると, \[ a\sqrt{(x-f)^2 + y^2} = a^2 - fx. \] 更に2乗して整理すると, \begin{eqnarray*} (a^2 - f^2)x^2 + a^2y^2 & = & a^2(a^2 - f^2), \\ \frac{x^2}{a^2} + \frac{y^2}{a^2 - f^2} & = & 1. \end{eqnarray*} よって, \[ b^2 = a^2 - f^2. \] と置けば,次の楕円の方程式を得ます. \[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1. \]
(2) 解法は以下のように3つ考えられます.
解1: \(s+t\) は一定の 2\(a\) ですので,その平均 \(\overline{s+t}\) も当然一定値の 2\(a\) です.一方, \(s\) と \(t\) は全く反対称に変化しますので,その平均値は等しく, \(\overline{s+t}\) の 1/2 となります.よって, \[ \overline{s} = \overline{t} = (\overline{s+t})/2 = a. \]
解2: \(s\) を \(x\) の式で表すことを考えます.上記の途中の式, \[ a^2y^2 = a^2(a^2 - f^2) - (a^2 - f^2)x^2. \] を,以下のように \(s\) を表す式へ代入して変形します. \begin{eqnarray*} s & = & \sqrt{(x+f)^2 + y^2}, \\ & = & (1/a)\sqrt{a^2(x+f)^2 + a^2y^2}, \\ & = & (1/a)\sqrt{a^2(x^2 + 2fx + f^2) + a^2(a^2 - f^2) - (a^2 - f^2)x^2}, \\ & = & (1/a)\sqrt{f^2x^2 + 2fa^2x + a^4}, \\ & = & (1/a)\sqrt{(fx + a^2)^2}, \\ & = & \frac{f}{a}x + a. \end{eqnarray*} よって, \(s\) は \(x\) の1次式で変化し,その平均は最小値と最大値の平均に等しくなるので, \[ \overline{s} = \frac{(a-f) + (a+f)}{2} = a. \]
解3: 解2と同じことですが,平均を厳密に求めると, \begin{eqnarray*} \overline{s} & = & \frac{\int_{-a}^{a}s dx}{\int_{-a}^{a}dx}, \\ & = & \frac{1}{2a}\int_{-a}^{a}\left(\frac{f}{a}x + a\right)dx, \\ & = & \frac{1}{2a}\left[\frac{f}{2a}x^2 + ax\right]_{-a}^a, \\ & = & a. \end{eqnarray*}