問題3−5−1 解答
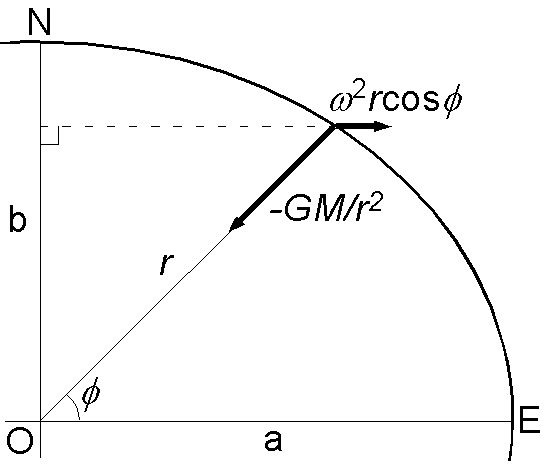
(1) 重力ポテンシャルの式, \[ V = -\frac{GM}{r} - \frac{1}{2}r^2\omega^2\cos^2\phi. \] を使用して,極 N と赤道 E で等しいとおき,式を変形します. \begin{eqnarray*} -\frac{GM}{b} & = & -\frac{GM}{a} - \frac{\omega^2}{2}a^2, \\ GM\left(\frac{1}{b}-\frac{1}{a}\right) & = & \frac{\omega^2}{2}a^2, \\ 1 - \frac{b}{a} & = & \frac{\omega^2}{2GM}a^2b. \end{eqnarray*} 右辺の \(M\) に,\(M = (4\pi/3)a^2b\rho\) を代入して, \[ f = 1 - \frac{b}{a} = \frac{3\omega^2}{8\pi G\rho}. \]
(2) 数値を代入して計算すると, \[ f = \frac{3\times (7.292\times 10^{-5})^2}{8\times 3.14\times 6.674\times 10^{-11}\times 5500} = 1.730\times 10^{-3} = \frac{1}{578}. \]
補足:より正しい地球の扁平率について
ホイヘンスが求めた扁平率と同じ値となりましたが,実際の地球楕円体の値は \(\sim\)1/298 です.1/578 という値がこれとかなり異なる理由は,上記の方法は地球の全質量が地球中心に集中していると仮定している点です.この仮定は球では成立しますが (問題3-5-2),回転楕円体には適用できません.この点を考慮して近似を高くした方法を → このページで解説しています.
問題3−5−2 解答
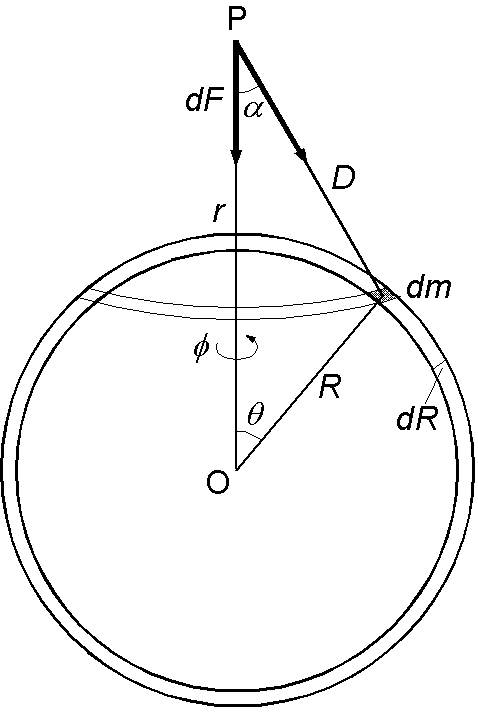
\(dF=\frac{G}{D^2}\cos\alpha dm\) を \(\phi\) は 0 から 2π, \(\theta\) は 0 から π, \(R\) は 0 から \(a\) まで積分します. \[ F = \int\int\int\frac{G}{D^2}\cos\alpha dm = \int_0^a dR\int_0^\pi d\theta\int_0^{2\pi}\frac{G}{D^2}\cos\alpha \rho R^2\sin\theta d\phi. \] \(\cos\alpha\) に余弦公式を適用して式を変形します. \begin{eqnarray*} F & = & 2\pi\rho G\int_0^a dR\int_0^\pi\frac{D^2+r^2-R^2}{2rD}\frac{1}{D^2}R^2\sin\theta d\theta, \\ & = & \frac{\pi\rho G}{r}\int_0^a dR\int_0^\pi\left(1+\frac{r^2-R^2}{D^2}\right)R^2\frac{\sin\theta}{D}d\theta. \end{eqnarray*} ここで, \(D=\sqrt{r^2 + R^2 - 2rR\cos\theta}\) を \(\theta\) で微分すると, \[ dD = \frac{rR\sin\theta}{\sqrt{r^2 + R^2 - 2rR\cos\theta}}d\theta = rR\frac{\sin\theta}{D}d\theta, \] 即ち, \[ \frac{\sin\theta}{D}d\theta = \frac{1}{rR}dD, \] の関係を使用して,積分変数を \(\theta\) から \(D\) へ変換します. \begin{eqnarray*} F & = & \frac{\pi\rho G}{r^2}\int_0^a dR\int_{r-R}^{r+R}\left(1+\frac{r^2-R^2}{D^2}\right)R dD, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a dR\left[D - \frac{r^2-R^2}{D}\right]_{r-R}^{r+R} R, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a dR\left(r+R-r+R-\frac{r^2-R^2}{r+R}+\frac{r^2-R^2}{r-R}\right)R, \\ & = & \frac{\pi\rho G}{r^2}\int_0^a R(r+R-r+R-r+R+r+R)dR, \\ & = & \frac{4\pi\rho G}{r^2}\int_0^a R^2 dR = \frac{4\pi\rho G}{r^2}\frac{a^3}{3} = \frac{GM}{r^2}. \end{eqnarray*}
補足:球殻の内部の点には力が働かないことについて
上図で,点 P が厚さ \(dR\) の球殻の内部(球殻で囲まれた空間)にある場合, P より上部の球殻による力と下部の球殻による力が相殺して,点 P には力が働かないことが予想されます.この場合,三角形 P-dm-O の角 \(\alpha\) が鈍角から鋭角まで変化しますが,上で導いた積分の式はそのまま使えます.但し, \(D\) の積分範囲が \(R-r\) から \(R+r\) となり,半径 \(R\),厚さ \(dR\) の球殻の全質量による力 \(dF\) は次の積分で与えられます. \[ dF = \frac{\pi\rho G}{r^2}\int_{R-r}^{R+r}\left(1+\frac{r^2-R^2}{D^2}\right)R dD. \]
この積分を上と同様に実行すると \(dF\) はゼロになることが分かります.この結果から,球の内部で半径 \(r\) に位置する質点に働く力は,その点より内側の部分の質量だけから力を受けることが分かります.球の密度を \(\rho\),質点は単位質量とすれば力は, \[ F = G\rho\frac{4\pi r^3}{3}\frac{1}{r^2} = \frac{4\pi\rho G}{3}r, \] となります.例えば,地球内部の重力は地球中心からの距離に比例し,中心でゼロになります.
問題3−5−3 解答
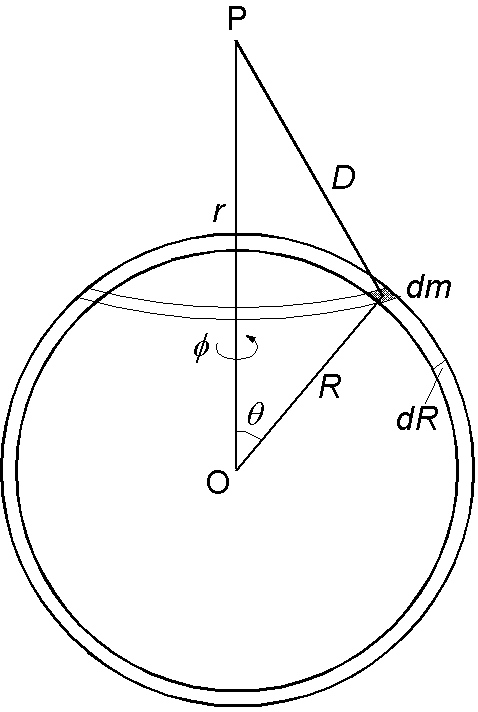
\(dV=-\frac{G}{D}dm\) を \(\phi\) は 0 から 2π, \(\theta\) は 0 から π, \(R\) は 0 から \(a\) まで積分します. \begin{eqnarray*} V & = & \int_0^a dR\int_0^\pi d\theta\int_0^{2\pi}-\frac{G}{D}\rho R^2\sin\theta d\phi, \\ & = & -2\pi\rho G\int_0^a dR\int_0^\pi R^2\frac{\sin\theta}{D}d\theta. \end{eqnarray*} ここで,前問と同様に \[ \frac{\sin\theta}{D}d\theta = \frac{1}{rR}dD \] の関係を使用して,積分変数を \(\theta\) から \(D\) へ変換します. \begin{eqnarray*} V & = & -\frac{2\pi\rho G}{r}\int_0^a RdR\int_{r-R}^{r+R}dD = -\frac{2\pi\rho G}{r}\int_0^a RdR[r+R-r+R], \\ & = & -\frac{4\pi\rho G}{r}\int_0^a R^2dR = -\frac{4\pi\rho G}{r}\frac{a^3}{3} = -\frac{GM}{r}. \end{eqnarray*} 得られた \(V\) は \(r\) だけの関数ですので,点 P における球の引力による加速度 \(g\) は, \[ g = -\frac{dV}{dr} = -\frac{d}{dr}\left(-\frac{GM}{r}\right) = -\frac{GM}{r^2}. \] 負の記号は加速度が \(-r\) の方向,球の中心を向いていることを示します.
補足:球殻の内部の点のポテンシャルは一定となることについて
球殻の内部の点(球殻で囲まれた空間に位置する点)には力が働かないこともポテンシャルを用いると式が簡単になります.厚さ \(dR\) の球殻の内部の点 P のポテンシャルは,上記で \(R\) で積分する前の式を \(D\) について \(R-r\) から \(R+r\) まで積分することで得られます. \[ dV = -\frac{2\pi\rho G}{r}R\int_{R-r}^{R+r} dD = -4\pi\rho GR. \] これは \(r\) に依存しない一定値ですので,球殻の内部の点 P には力は働きません.例えば,厚さ \((b-a)\) の球殻で囲まれた空間内の任意の点のポテンシャルは,これを \(R\) で積分して, \[ V = -4\pi\rho G\int_a^b R dR = -2\pi\rho G(b^2-a^2), \] となり, \(-\nabla V=0\) となります.