問題3-1-2 解説
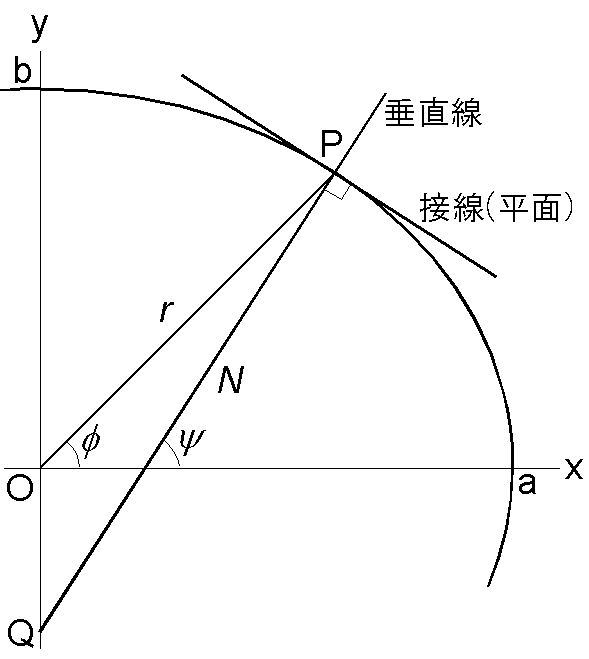
(1) \(x=r\cos\phi\) と \(y=r\sin\phi\) を楕円の方程式, \begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \label{eq01} \end{equation} に代入します. \begin{eqnarray*} r^2 & = & \frac{a^2b^2}{b^2\cos^2\phi + a^2\sin^2\phi}, \\ & = & \frac{a^2b^2}{a^2 - (a^2-b^2)\cos^2\phi}, \\ & = & \frac{b^2}{1 - \left(1-\frac{b^2}{a^2}\right)\cos^2\phi}. \end{eqnarray*} これに \(e^2=1-b^2/a^2\) を代入して, \[ r = \frac{b}{\sqrt{1-e^2\cos^2\phi}}. \]
(2) 楕円の式(1)を \(x\) で微分して, \(2b^2x+2a^2y(dy/dx)=0\) より, \[ \frac{dy}{dx} = -\frac{b^2}{a^2}\frac{x}{y} = -\frac{b^2}{a^2}\frac{1}{\tan\phi}. \] PQ の傾き \(\tan\psi\) と点 P での接線の傾き \(dy/dx\) は直交するので, \[ \tan\psi\frac{dy}{dx} = -\frac{b^2}{a^2}\frac{\tan\psi}{\tan\phi} = -1. \] よって, \begin{equation} \tan\phi = \frac{b^2}{a^2}\tan\psi. \label{eq02} \end{equation}
(3) 図から, \(r\cos\phi = N\cos\psi\).この関係式を2乗して, \begin{eqnarray*} N^2 & = & r^2\frac{\cos^2\phi}{\cos^2\psi}, \\ & = & \frac{b^2}{1 - \left(1-\frac{b^2}{a^2}\right)\cos^2\phi}\times\frac{\cos^2\phi}{\cos^2\psi}, \\ & = & \frac{b^2}{\frac{1}{\cos^2\phi} - 1 + \frac{b^2}{a^2}}\times\frac{1}{\cos^2\psi}, \\ & = & \frac{b^2}{\tan^2\phi+\frac{b^2}{a^2}}\times\frac{1}{\cos^2\psi}. \end{eqnarray*} これに式(2)を2乗した \(\tan^2\phi=(b^4/a^4)\tan^2\psi\) を代入して, \begin{eqnarray*} N^2 & = & \frac{a^2}{\frac{b^2}{a^2}\tan^2\psi + 1}\times\frac{1}{\cos^2\psi}, \\ & = & \frac{a^2}{\frac{b^2}{a^2}\sin^2\psi + \cos^2\psi}, \\ & = & \frac{a^2}{1-\left(1-\frac{b^2}{a^2}\right)\sin^2\psi}. \end{eqnarray*} よって, \[ N = \frac{a}{\sqrt{1 - e^2\sin^2\psi}}. \]