問題3-1-1 解説
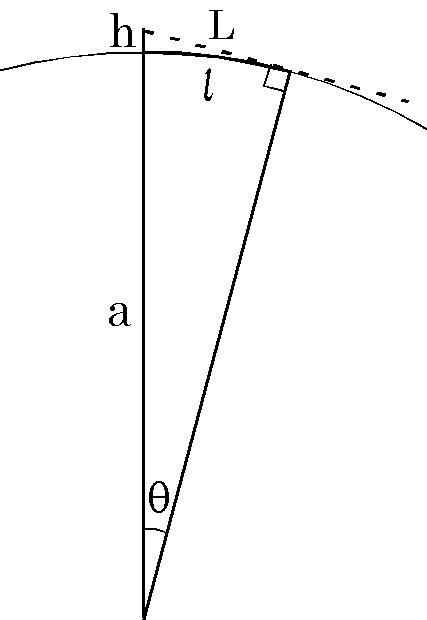
右の地球の断面図で,円弧の距離 \(\ell\) は,ラジアンで表した角度 \(\theta\) を用いて, \[ \ell = a\theta, \] ですが, \(\theta\) については, \[ \cos\theta = \frac{a}{a+h}, \] となります.左辺を \(|\theta| \ll 1\) として近似し,右辺も変形して, \begin{eqnarray*} 1 - \frac{1}{2}\theta^2 & \approx & 1 - \frac{h}{a+h}, \\ \theta & \approx & \sqrt{\frac{2h}{a+h}}. \end{eqnarray*} 以上より, \[ \ell = a\sqrt{\frac{2h}{a+h}}. \] 因みに,近似しない真の距離 \(\ell_0\) と直線距離 \(L\) は次のようになります. \begin{eqnarray*} \ell_0 & = & a \cos^{-1}\left(\frac{a}{a+h}\right), \\ L & = & \sqrt{h(h+2a)}. \end{eqnarray*} これらを \(a\) を 6400 km,\(h\) を 1 m,10 m,... として計算し,有効数字5桁まで取り表にまとめてみます.
| \(h\) [m] | \(\ell_0\) [km] | \(\ell\) [km] | \(L\) [km] |
| 1 | 3.5777 | 3.5777 | 3.5777 |
| 10 | 11.314 | 11.314 | 11.314 |
| 100 | 35.777 | 35.777 | 35.777 |
| 1000 | 113.13 | 113.13 | 113.14 |
全ての場合で,近似した値は真値と一致しています.直線距離も,高さが 1 km になって初めて円弧距離との差が現れます.これらのことは逆に言えば,普通の生活上の感覚からは地球が巨大であることを示唆していると考えられます.