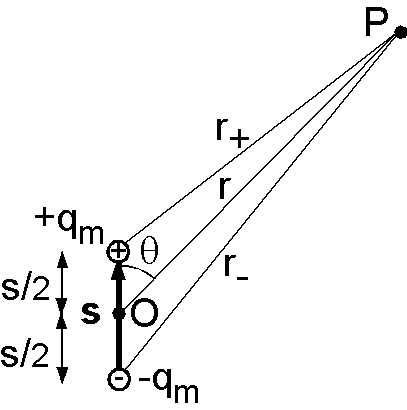
問題6-2-2 解説
図のような2つの正負の磁荷 \(\pm q_m\) による点 P のポテンシャル \(W\) を, OP の距離 \(r\) で表わす式を導きます.まず, \(+q_m\) と \(-q_m\) と P との距離 \(r_+\) と \(r_-\) を用いて, \(W\) は次式で表わされます. \[ W = \frac{\mu_0 q_m}{4\pi}\left(\frac{1}{r_+} - \frac{1}{r_-}\right). \] これを, \(r_+\) と \(r_-\) を余弦定理から \(r\), \(\theta\), \(s\) で表わし, \(r \gg s\) として近似する式の変形は次の通りです. \begin{eqnarray*} W & = & \frac{\mu_0 q_m}{4\pi}\left(\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2-2r\frac{s}{2}\cos\theta}} -\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2+2r\frac{s}{2}\cos\theta}}\right), \\ & = & \frac{\mu_0 q_m}{4\pi r}\left(\frac{1}{\sqrt{1+\frac{s^2}{4r^2}-\frac{s}{r}\cos\theta}} -\frac{1}{\sqrt{1+\frac{s^2}{4r^2}+\frac{s}{r}\cos\theta}}\right), \\ & \approx & \frac{\mu_0 q_m}{4\pi r}\left(1-\frac{s^2}{8r^2}+\frac{s}{2r}\cos\theta -1+\frac{s^2}{8r^2}+\frac{s}{2r}\cos\theta\right), \\ & = & \frac{\mu_0}{4\pi}\frac{q_ms\cos\theta}{r^2}. \end{eqnarray*} ここで, \(q_ms\) を一定の値 \(M\) に保ちながら \(q_m\rightarrow\infty\), \(s\rightarrow 0\) とした極限が磁気双極子で, \(M\) を磁気双極子モーメントといいます.結局,磁気双極子のポテンシャルは次式となります. \[ W = \frac{\mu_0}{4\pi}\frac{M\cos\theta}{r^2}. \] また,ベクトル \({\bf s}\) を用いて,磁気双極子モーメントを, \[ {\bf M} = q_m{\bf s}, \] で表わされるベクトルとして考えることができます.上の導出においては,ベクトル \({\bf s}\) の向きや点 P の位置は任意ですので,ポテンシャルの一般的な式は点 P の位置ベクトルを \({\bf r}\) として,次式となります. \[ W = \frac{\mu_0}{4\pi}\frac{{\bf M}\cdot{\bf r}}{r^3}. \]