問題2-4 解説
解1: 放射性元素の数 \(N\) は,初期値を \(N_0\) とすると,時間 \(t\) ともに次式に従って減少します. \[ N = N_0 e^{-\lambda t}. \] 時刻 \(t\) において,微小時間 \(dt\) の間に崩壊する放射性元素の数 \(dn\) は次式で与えられます. \[ dn = -\frac{dN}{dt}dt = N_0\lambda e^{-\lambda t}dt. \] このことは,時刻 \(t\) の時点で寿命が \(t\) の放射性元素の数が \(dn\) 個であったことを意味します.よって, \(t\times dn\) を全時間について積分し, 同様に \(dn\) を積分した総数で割れば平均寿命 \(\overline{T}\) となります. \begin{eqnarray*} \overline{T} & = & \frac{\int_{t=0}^\infty t dn}{\int_{t=0}^\infty dn}, \\ & = & \frac{N_0\int_0^\infty t\lambda e^{-\lambda t}dt}{N_0\int_0^\infty \lambda e^{-\lambda t}dt}, \\ & = & \frac{\left[-t e^{-\lambda t}\right]_0^\infty + \int_0^\infty e^{-\lambda t}dt}{\int_0^\infty \lambda e^{-\lambda t}dt}, \\ & = & \frac{\frac{1}{\lambda}\left[-e^{-\lambda t}\right]_0^\infty}{\left[-e^{-\lambda t}\right]_0^\infty}, \\ & = & \frac{1}{\lambda}. \end{eqnarray*} 以上,計算の途中で部分積分の公式を使用しました.なお,分母の \(dn\) の積分は \(N_0\) になることは明らかですので省略できます.また, \(t=\overline{T}\) で, \[ N = N_0 e^{-\lambda\overline{T}} = \frac{N_0}{e}, \] となり,放射性元素の平均寿命とは元素の数が \(1/e\) に減少する時間であることが分かります.放射性元素の特性を表すのに半減期よりは寿命を使用する学問分野もあるようです.
解2: \((N_0-N)/N_0\) は時間 \(t\) の間に崩壊する放射性元素の割合を表わします.この量は,1つの放射性元素が崩壊する確率という観点から見ると,時間 \(t\) の間に崩壊する確率 \(P\) (正確には累積確率)を表します.そこで,元素の寿命 \(T\) を確率変数と考えれば,次式は \(T\) が \(t\) 以下である累積確率を表す累積分布関数となります. \[ F(t) = P\{T\leq t\} = \frac{N_0-N}{N_0} = 1 - e^{-\lambda t}. \] 一方,時刻 \(t\) において放射性元素が崩壊する確率を表す確率密度関数 \(f(t)\) は \(F(t)\) を微分して得られますので次式となります. \[ f(t) = dF(t)/dt = \lambda e^{-\lambda t}. \] よって,放射性元素の平均寿命は次のようにして求められます. \begin{eqnarray*} \overline{T} & = & \int_0^\infty tf(t)dt, \\ & = & \int_0^\infty t \lambda e^{-\lambda t}dt, \\ & = & \left[-t e^{-\lambda t}\right]_0^\infty + \int_0^\infty e^{-\lambda t}dt, \\ & = & \frac{1}{\lambda}\left[-e^{-\lambda t}\right]_0^\infty, \\ & = & \frac{1}{\lambda}. \end{eqnarray*}
補足:確率密度と関数の平均について
上で \(t\) の平均を求めた方法について,正確さは欠けますが平易な説明は以下の通りです.試験の成績表から平均点を求める方法を考えます. \(i\) は表の列番号, \(x_i\) は得点, \(n_i\) は成績が \(x_i\) だった生徒の人数, \(f_i\) は \(n_i\) を生徒の総数 25 で割って規格化した値, \(F_i\) は \(f_i\) を \(i\)=1 から \(i\) まで合計した値です.
| \(i\) | 1 | 2 | 3 | 4 | 5 |
| \(x_i\) | 50 | 60 | 70 | 80 | 90 |
| \(n_i\) | 3 | 5 | 8 | 7 | 2 |
| \(f_i\) | 3/25 | 5/25 | 8/25 | 7/25 | 2/25 |
| \(F_i\) | 3/25 | 8/25 | 16/25 | 23/25 | 25/25 |
一般には得点の平均は次のように求めます. \[ \overline{x} = \frac{50\times 3 + 60\times 5 + 70\times 8 + 80\times 7 + 90\times 2}{3+5+8+7+2} = \frac{1750}{25} = 70. \] 式で表すと次式となります. \begin{equation} \overline{x} = \frac{\sum_{i=1}^5 x_i n_i}{\sum_{i=1}^5 n_i}. \end{equation} 一方,得点の平均は次のようにしても得られます. \begin{eqnarray*} \overline{x} & = & 50\times\frac{3}{25} + 60\times\frac{5}{25} + 70\times\frac{8}{25} + 80\times\frac{7}{25} + 90\times\frac{2}{25}, \\ & = & 6+12+22.4+22.4+7.2 = 70. \end{eqnarray*} 式で表すと次式となります. \begin{equation} \overline{x} = \sum_{i=1}^5 x_i f_i. \end{equation} ここで,得点を確率変数 \(X\) と考えると, \(X=x\) となる確率を表す確率密度関数 \(f(x)\) と \(X\leq x\) となる累積確率を表す累積分布関数 \(F(x)\) のグラフは図のようになります.
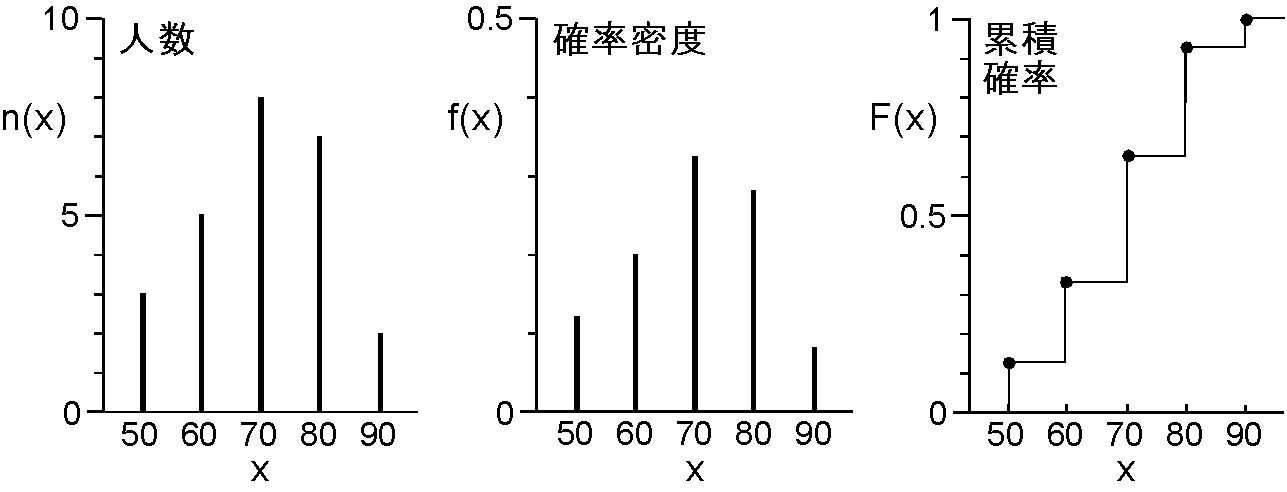
上記の問題の解は \(x_i\) を連続変数に拡大した場合と考えれば良く,解1は式 (1) を,解2は式 (2) を積分の形に拡大して利用したものです.特に確率密度関数を使用すれば関数の平均も求めることができます.例えば,定義域が \([a,b]\) である \(x\) の関数 \(g(x)\) の平均は, \begin{equation} \overline{g(x)} = \int_a^b g(x)f(x)dx, \end{equation} で求められます.但し, \(f(x)\) は \(x\) の確率密度関数で, \begin{equation} \int_a^b f(x)dx = 1, \end{equation} を満たす必要があります.