以上、見てきたように、非対称静電力を使用する新型静電発電機の原理も、その構造も簡明で何ら問題
はないように見えます。しかし、最後に、大きな疑問が残されています。
それは、電界のエネルギーに関する疑問です。
通常、静電気の教科書では、電界は電気のエネルギーを蓄えている、と記述されています。
そして、その部分の電気エネルギーが消費されると、その部分からは、もう電気のエネルギーを得る
ことができない、と説明されています。
　例えば、先に紹介した、「物理学の基礎」[1]に次のような例題があります。（例題２６−５、P.88)
「電気容量Cが13.5μFの平行極板キャパシターを電位差V=12.5Vの電池で充電した後、電池を取り外して、
板状の磁器（κ=6.5）を電極板間に差し込んだ。磁器の板を差し込む前後でのキャパシターの
ポテンシャルエネルギーはいくらか？」
解答は、磁器を差し込む前、1055pJ、後　162pJ です。このあと、次のような記述があります。
「誘電体を挿入した人はおそらく”失われた”エネルギーを感じ取ることができたであろう。
キャパシターが誘電体板をわずかに引っ張り、板に対して仕事をする；その量は
　　　　　W＝（1055-162）pJ=893pJ
拘束力も摩擦もない状態で板が電極板間に滑り込むならば、板は電極板間を出たり入ったり振動する。
このときの力学的エネルギーは一定値893pJであり、振動する板の運動エネルギーと電場に蓄えられるポテンシャルエネルギーの間で行ったり来たりする。」

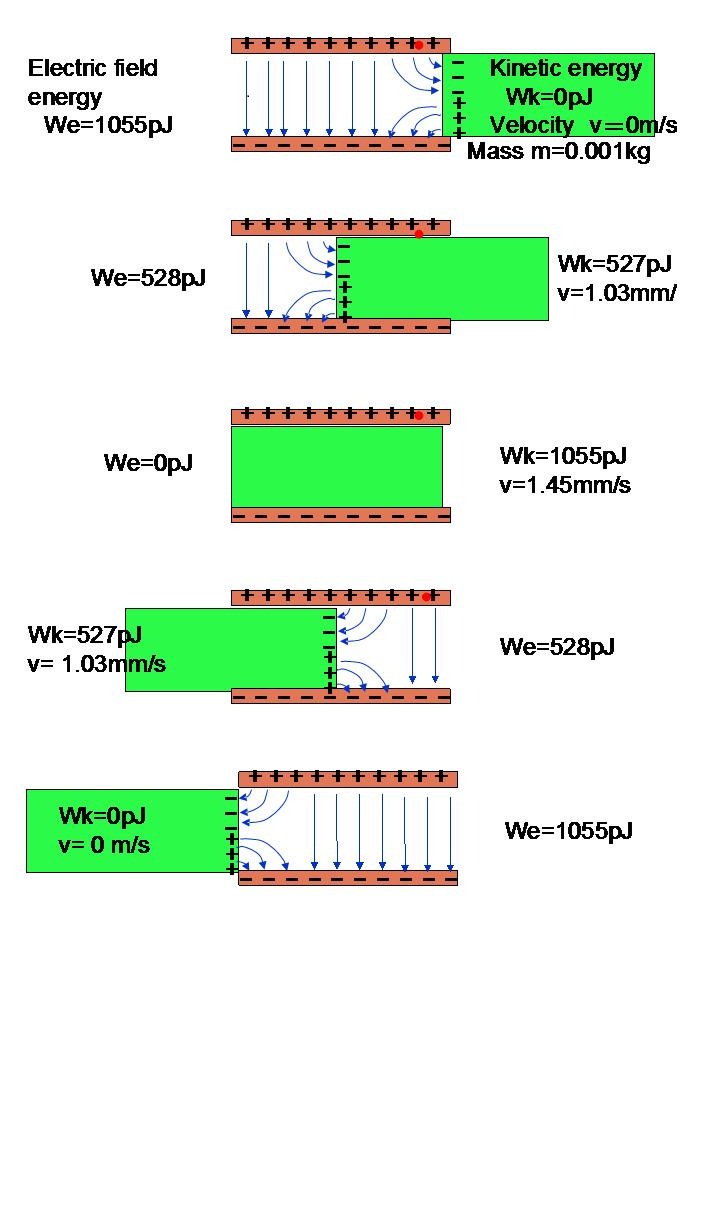
　この記述のみでは分かりにくいと思われるので具体的な説明を加えます。図２９において、上下の黄銅色
の平行平板がキャパシターを構成する電極です。その中に、正と負の電荷が分布しています。
緑色の立方体が、磁器に代わる導体です。導体の方が分かりやすいと考えて置き換えました。もちろん、
電極板との間は薄い絶縁膜で絶縁されています。この導体の質量は１グラムとします。
青い矢印は、電気力線です。導体の影響の無い左側では、電気力線は、上から下に垂直に伸びています。
しかし、導体の近くでは、導体側面に静電誘導された対抗電荷に曲がって行きます。そして、導体の側面に垂直に入ります。その結果、導体の左側面に、これを左方向に引く静電力が発生します。
　左方向に徐々に進んで、導体の左側面が電極板の中央まで来たとき、キャパシターの蓄えていたポテンシャルエネルギー（We）1055pJの半分、527pJが、導体の運動エネルギーWkに変換されます。
この時の、導体の速度vは、1.03mm/sです。
　さらに、進んで、導体の左側面が、電極板の左端に到達すると、ポテンシャルエネルギーWeはゼロとなり、全て、導体の運動エネルギーWkに変換されます。この時の、速度が最大値になり1.45mm/sです。
この時、導体をさらに左に引く静電力はありません。しかし、導体は慣性の法則で、さらに左に進みます。
この時、速度は徐々に遅くなります。導体の右端が電極板の真ん中に来たとき、その速度は、1.03mm/sまで
遅くなります。この間に、導体が失った運動エネルギーWkは、527pJです。このエネルギーは、キャパシターの右半分のポテンシャルエネルギーWe　527pJ　に変換されました。
　導体がさらに進み、その右側面が、電極板の左端に到達した時、その速度はゼロになります。
この間に失われた運動エネルギーWk528pJは、キャパシターの左半分のポテンシャルエネルギーに変換されています。この地点で、導体の速度はゼロになったのですが、図のように、今度は右方向に引く静電力が 発生するので、右方向に動き始めます。そして、その左側面が電極板の右橋に到達すると、その速度はゼロ となります。この状態は、図１の再上図と同じです。故に、また、左方向に反転して向かい、この動きが限りなく繰り返されます。
　以上が、補足説明です。この見方によれば、電界のエネルギーは、一度使われると、つまり運動エネルギーに変換されると、他の何らかのエネルギーで補わなければ再生しないことになります。
これは本当でしょうか？
この疑問に答えるために簡単な実験が計画されて実行されました。

図２９、平行平板電極内に無帯電導体が静電力で引き込まれる図

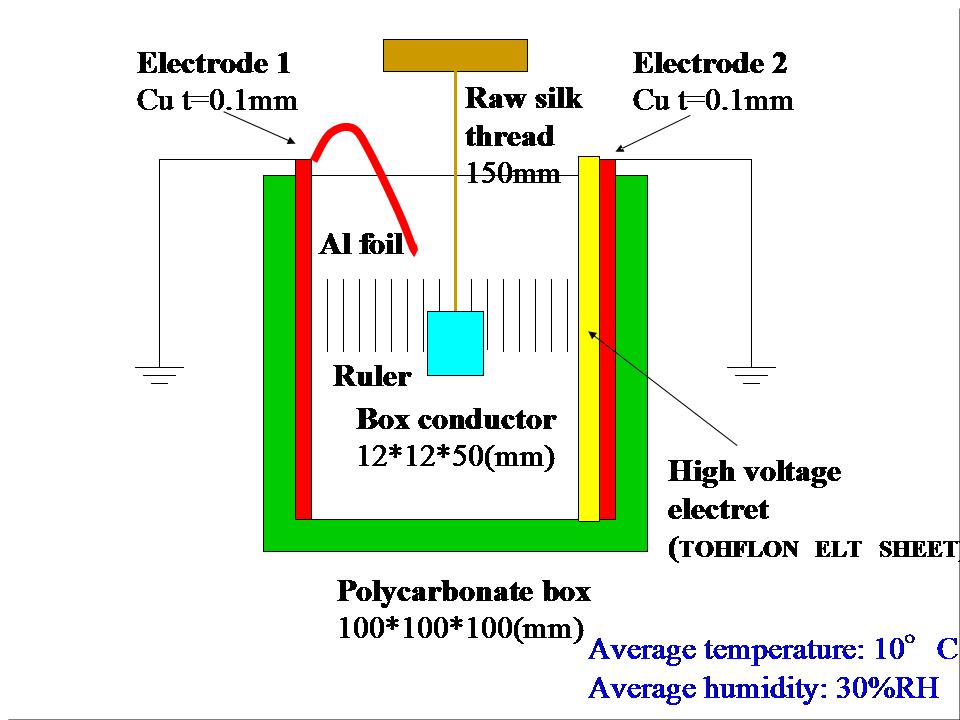
図３０は実験装置の正面図です。
この装置は、２枚の平行電極と、エレクトレットと箱型導体で構成されています。それらは、ひとつの大きな箱の中に収められます。
透明の大きなポリカーボネイト製の箱が用意されました。この箱は、外部から吹き寄せる風から小さな箱型導体を守ります。
この実験は外部環境の下で行われました。なぜならば、この実験は低湿度を必要としたからです。残念ながら、私は低湿実験室を持っていませんでした。そこで、この実験は、この冬の快晴の日に,窓を開けた状態で行われました。当日の、平均気温は１０°C、平均湿度は、30%RHでした。
たてよこ100mm、厚さ0.1mmの薄い銅板が、左右の電極として大きな箱の左右の壁にはりつけられました。その間の距離は、100mmです。両電極は接地されました。
箱型導体は長さ150mmの絶縁性の生糸で両電極の真ん中に吊り下げられました。箱型導体の、幅、高さ、長さはそれぞれ、12mm、12mm、50mmでした。その材質はアルミで、厚さは0.1mmでした。
両電極と箱型導体のエッジは、そこで放電が発生しないように、目の細かいサンドペーパーで磨かれました。
エレクトレット (TOHFLON　ELT　SHEET 東邦化成�叶ｻ) が右の電極に張り付けられました。この特殊なエレクトレットは、高電圧源として使用されました。その電位は　ー14kVでした。
通常、この高電位は１枚のエレクトレットシートでは得られないので、４枚重ねで使用されました。各シートの電位は、ー3.5kVで、表面電荷密度は、約ー0.8mC/m2でした。なお、各シートの厚さは75ミクロンで、その材質はフッ素樹脂です。

図３０、実験装置正面図

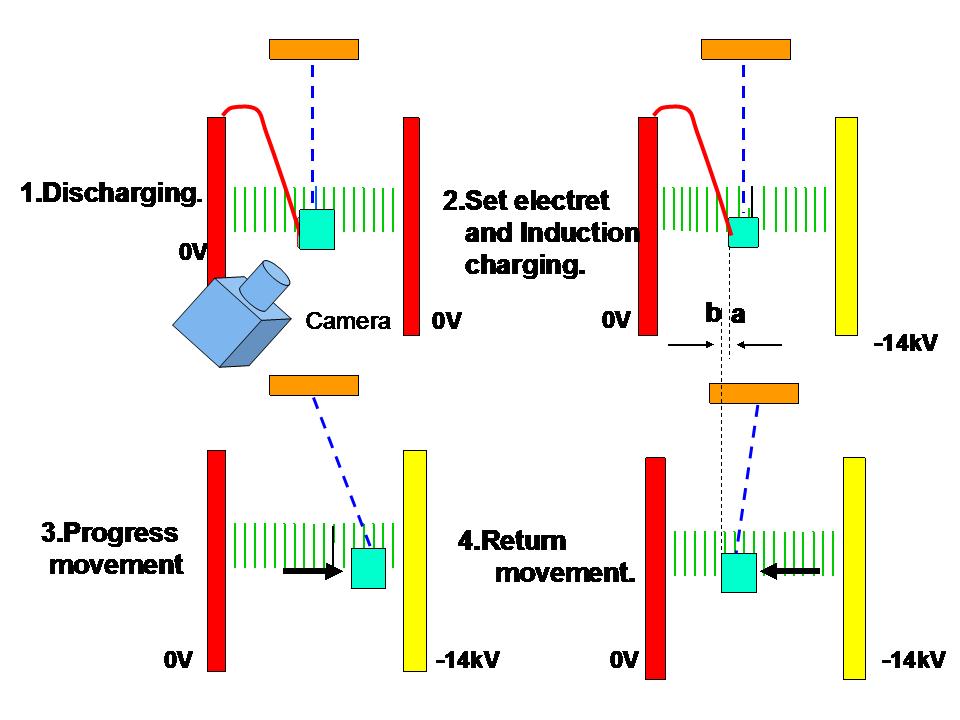
図３１は実験手順の説明図です。
実験は下記の手順にしたがって実行されました。
�@.左右の電極は接地されます。そして、箱型導体に、その除電のために、接地されたアルミフォイルが軽く接触します。
�A.エレクトレットが右の電極に重ねられます。そして、そこに電荷注入するために、箱型導体に、接地されたアルミフォイルが再度軽く接触します。この位置を、図３１に描かれているように出発点 "a" と定義します。
�B.箱型導体に正電荷が注入されたため、該箱型導体は、そこに働く静電気力によって、右方向へ前進します。
�C.その後、該箱型導体は、そこに働く糸の張力によって、左方向へ後退させられます。その後退動作が終わる位置を、図３１に描かれているように、引き返し点"b"と定義します。
�D.最後に、出発点"a"と引き返し点"b"の距離が、実験を記録した動画の画面から測定されます。 この距離、a-b をオーバーラン距離と呼ぶことにします。

この実験は４８回繰り返されました。この実験結果は、次に行うシミュレーションの結果と合わせて、後で、同じ図に表示されます。

図３１；実験手順の説明図

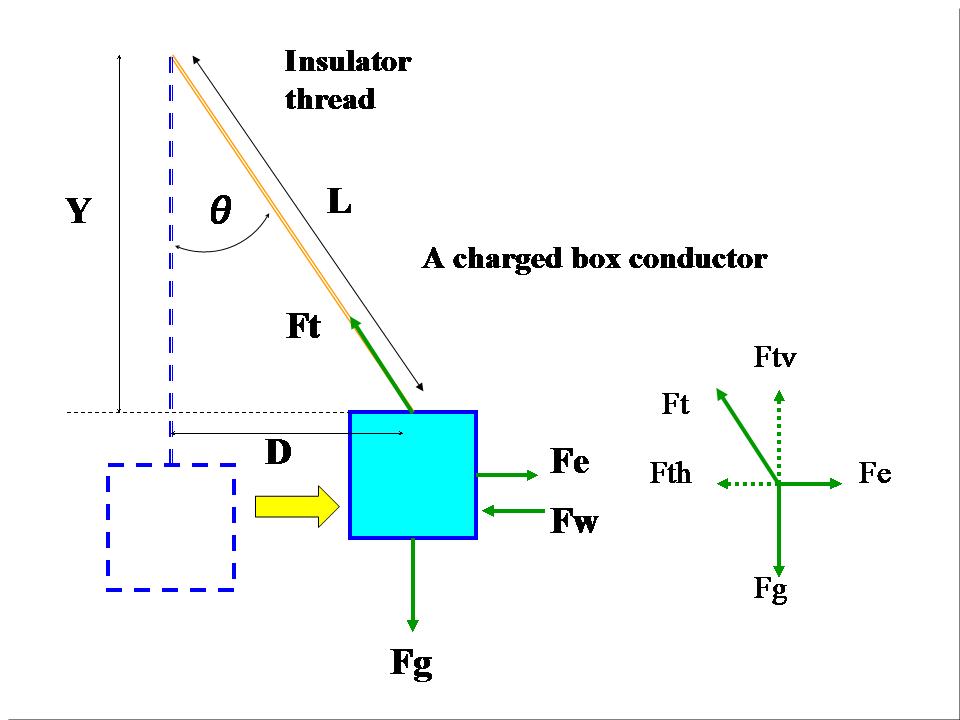
図３２は、帯電した箱型導体に働く４つの力を示しています。
動いている帯電した箱型導体に働く４つの異なった力があります。
すなわち、それらは、静電気力 fe、重力 fg、張力 ft、そして空気抵抗力 fwです。
静電気力の方向は、X軸のプラス方向です。一方、張力の水平成分と空気抵抗力の方向はX軸のマイナス方向です。
また、張力の垂直成分の方向は、Y軸のプラス方向で、重力の方向はY軸のマイナス方向です。そして、この二つの力の大きさは常に同じです。
その結果、この帯電した箱型導体に働くY軸方向の力はありません。それゆえ、この帯電した箱型導体は、静電気力と張力の水平成分と空気抵抗力を合わせた総合力で水平に動かされます。
静電気力は二次元差分法でシミュレーションされました。この方法の詳細は以前にこの学会で報告済みです。[2] [3].　それゆえ今回はその最終結果のみ報告します。
この箱型導体中に誘導（注入）された電荷量は、-6.72nCとシミュレーションされました。その結果、この帯電した箱型導体に働く静電気力は、0.722mNとシミュレーションされました。
張力の水平成分の大きさ Fth は、箱型導体の移動距離　D　と、糸の長さ　L　と、重力　fg　より次の式で求められます。

図３２：前進移動中の帯電した箱型導体に働く静電気力、張力、重力、空気抵抗力の模式図。

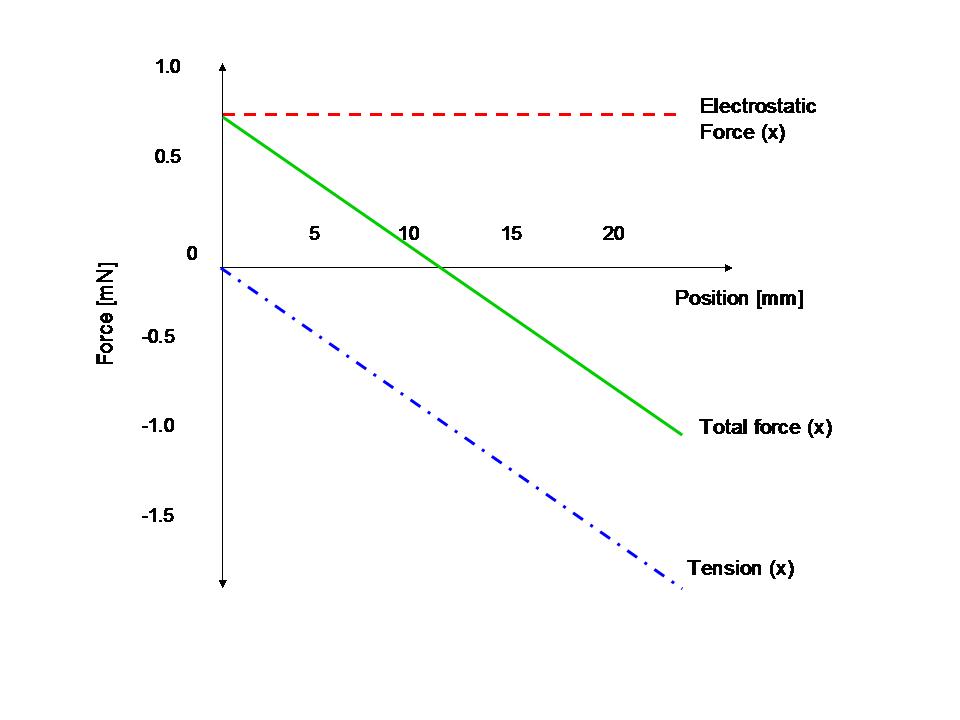
図３３は、帯電した箱型導体に働く、シミュレーションされた静電気力と、式（１）より計算された張力の水平成分と総合力を示します。
空気抵抗力はこの図に入れませんでした。なぜならば、その大きさがあまりにも小さかったからです。
図３３から、この帯電された箱型導体は、0-11mm間で加速され、11-22mm間で減速されることは明らかです。
この帯電された箱型導体の速度は、そこに働く総合力を用いて、運動方程式を解くことで求められました。

図３３：帯電した箱型導体に働く、静電気力、と張力、と総合力。

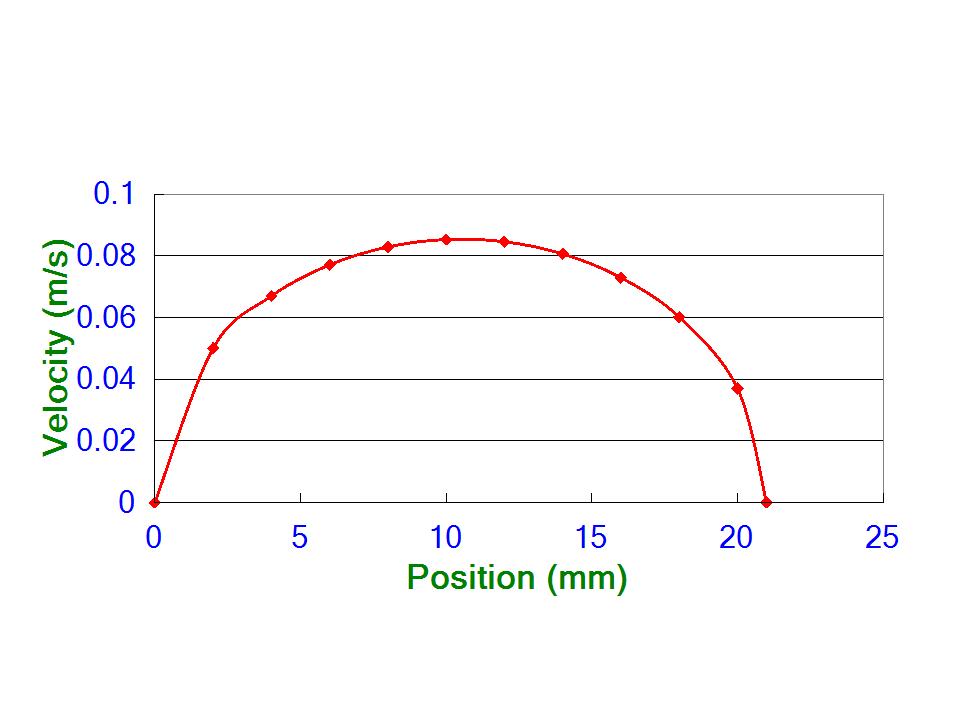
図３４は帯電された箱型導体の速度の計算結果を示します。この図から、その速度は、距離11mmで最高になり、その後、減速して距離22mmでゼロになることが分かります。この地点で、該箱型導体は一度停止しすぐ左方向へ戻り始めます。
この復路において、先に該帯電された箱型導体が通り過ぎた部分の電界のエネルギーは失われているかもしれません。
その場合、復路の電界のエネルギー分布には、３つのケースが考えられます
図３５は、その３ケースのエネルギー分布と、最初の、すなわち、往路のエネルギー分布を示しています。

図３４：帯電された箱型導体に働く総合力で計算された、該箱型導体の速度。

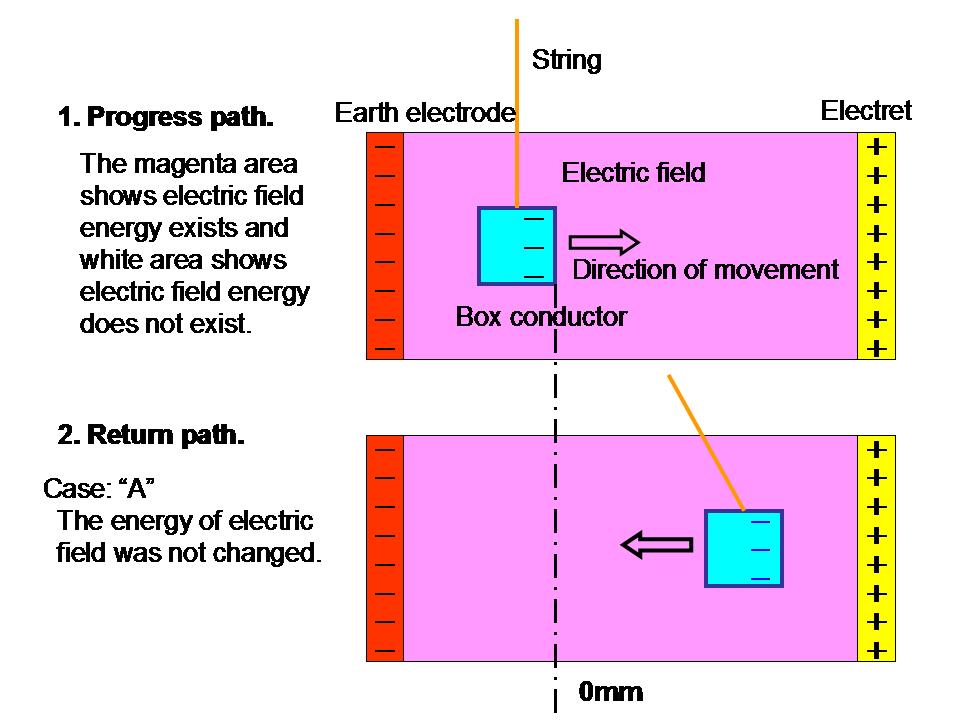
これらの絵の中でマゼンタ色の部分は電界のエネルギーが存在するところ、そして白色の部分はエネルギーが存在していないところを示しています。
一番目の絵は、もともとのエネルギー分布を示しています。電極間のすべての領域に電界のエネルギーが存在しています。
二番目の絵は、帯電された箱型導体の復路の、ケースAの場合のエネルギー分布を示しています。ケースAとは、往路で、該箱型導体が通過した領域で、そのエネルギーが箱型導体の運動エネルギーに使用されても、電界が変化しなかった場合です。 もちろん、通過したすべての領域で電界のエネルギーは存在しています。
三番目の絵は、ケースBを示します。ケースBとは、往路で箱型導体の通過した領域の電界のエネルギーが全て運動エネルギーに転換され電界が消滅した場合です。もちろん、電界のエネルギーは残っていません。
最後の絵は、ケースCを示します。ケースCでも、箱型導体の往路に当たる電界は変化します。
往路の前半では、箱型導体は加速運動をします。それゆえ、そこには電界のエネルギーは残りません。
一方、後半では、減速運動するので、機械的エネルギーが、電界のエネルギーに戻されて電界が復活します。なお、もともとそこにあった電界のエネルギーは、該箱型導体に静電力を加えたため消滅しています。
前半の加速運動と後半の減速運動は図３４より明らかです。

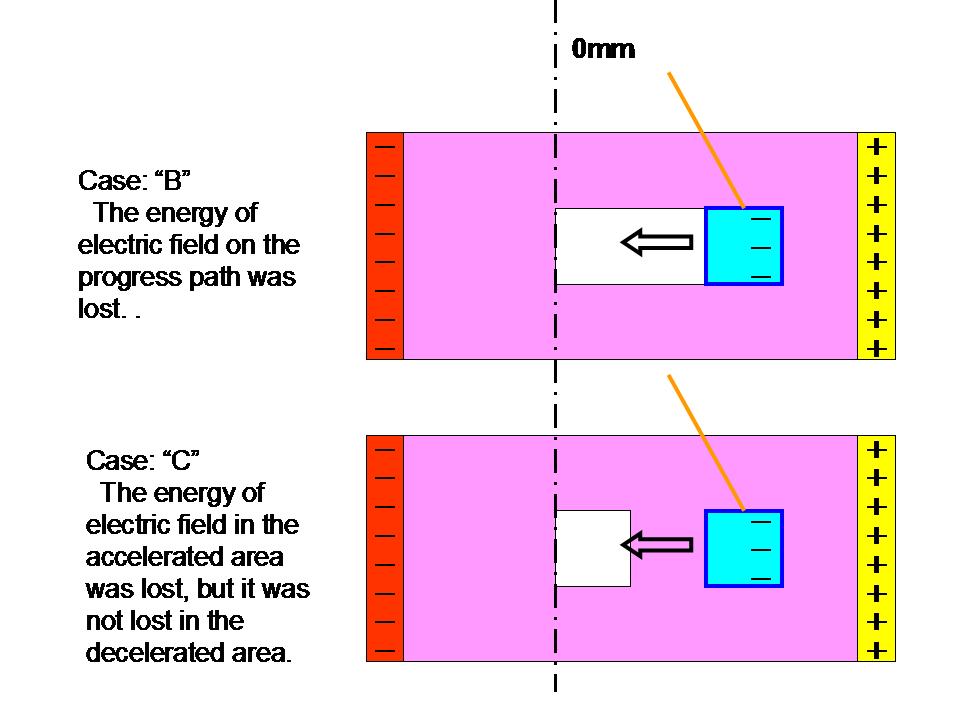
図３５：往路上のもともとの電界のエネルギー分布と、復路上の、可能性のある３つの電界エネルギー分布。

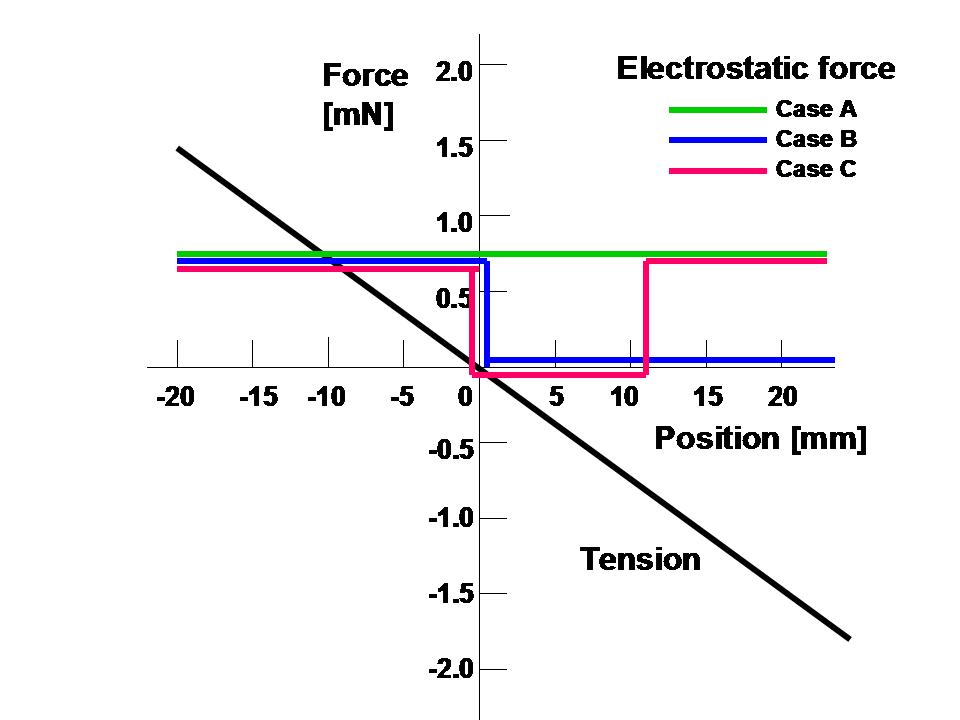
図３６は、３つの電界エネルギー分布に対応して該帯電された箱型導体に復路で働く静電気力と、 式（１）により計算された張力の水平成分と、それらを合わせた（空気抵抗力も含む）総合力をしています。
空気抵抗力は、非常に小さいため、この図では表示していません。
図３６より、ケースAの場合、総合力で駆動される該帯電された箱型導体は、出発点（0mm）よりの距離が、22mmから11mmにかけて、次第に加速され、11mmから0mmにかけて次第に減速されることが分かります。
これに反して、ケースBの場合は、それは、22mmから11mmにかけてより強く加速され、11mmをすぎても0mmまでも、加速され続けることが分かります。
一方、ケースCの場合は、22mmから11mmにかけて次第に加速され、１１mmから0mmにかけて再度次第に加速されることが分かります。
この３ケースの場合の該帯電された箱型導体の速度が運動方程式を解くこと計算されました。
図３７はこの結果をしめしています。

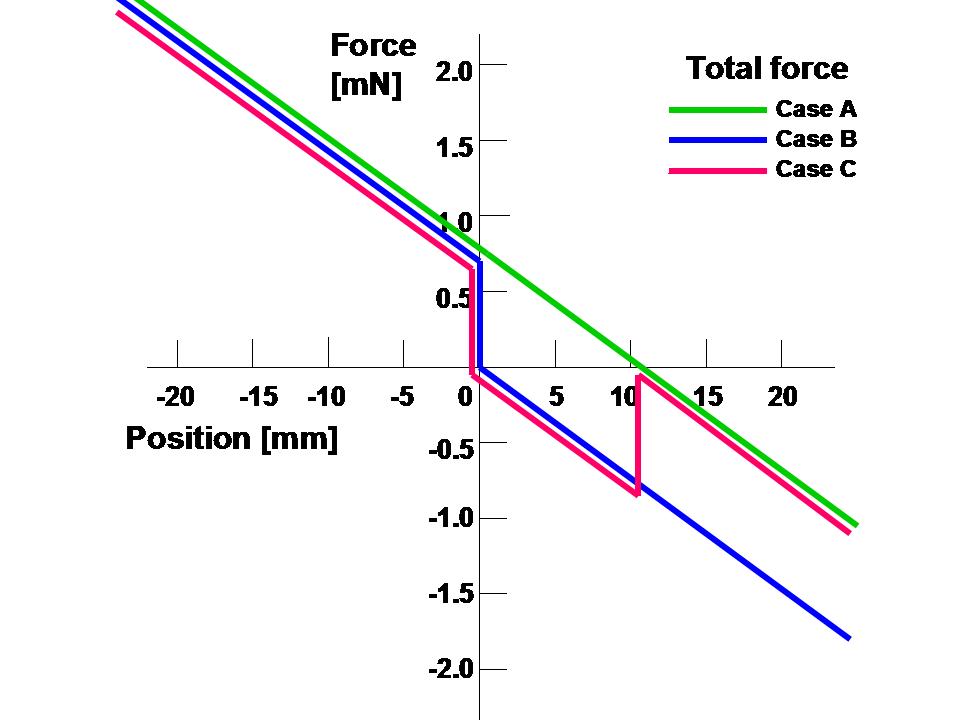
図３６：可能性のある３つの電界のエネルギー分布に対応して、該帯電された箱型導体に働く静電気力と、計算された張力の水平成分と総合力。

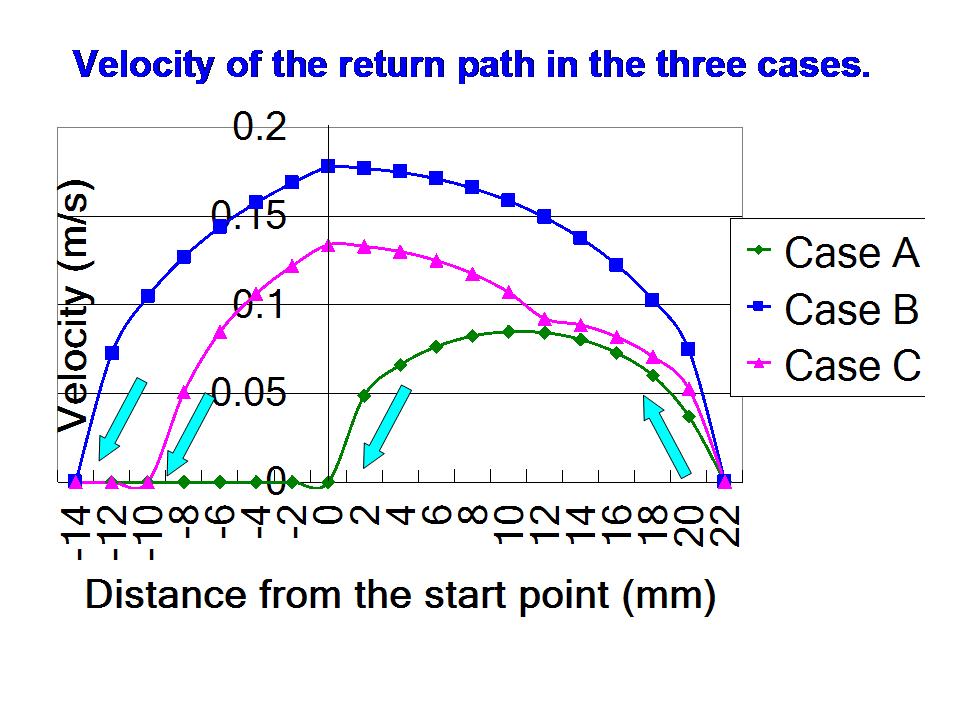
図３７より、ケースAの場合には、帯電された箱型導体は、出発点(0mm）に戻ることは明らかです。
これに対して、ケースBとケースCの場合には、出発点を大きく通りすぎる、オーバーランすることが分かります。
オーバーランの距離は、ケースBの場合、14mmで、ケースCの場合、10mmです。
実際の、オーバーラン距離は、先に紹介した簡単な実験装置で測定されました。
図３８は、シミュレーションで求められた３ケースのオーバーラン距離と、４８回の実験で求められた４８個のオーバー欄距離を示しています。

図３７：復路上の３ケースの電界エネルギー分布に対応して計算された帯電された箱型導体の復路の速度。

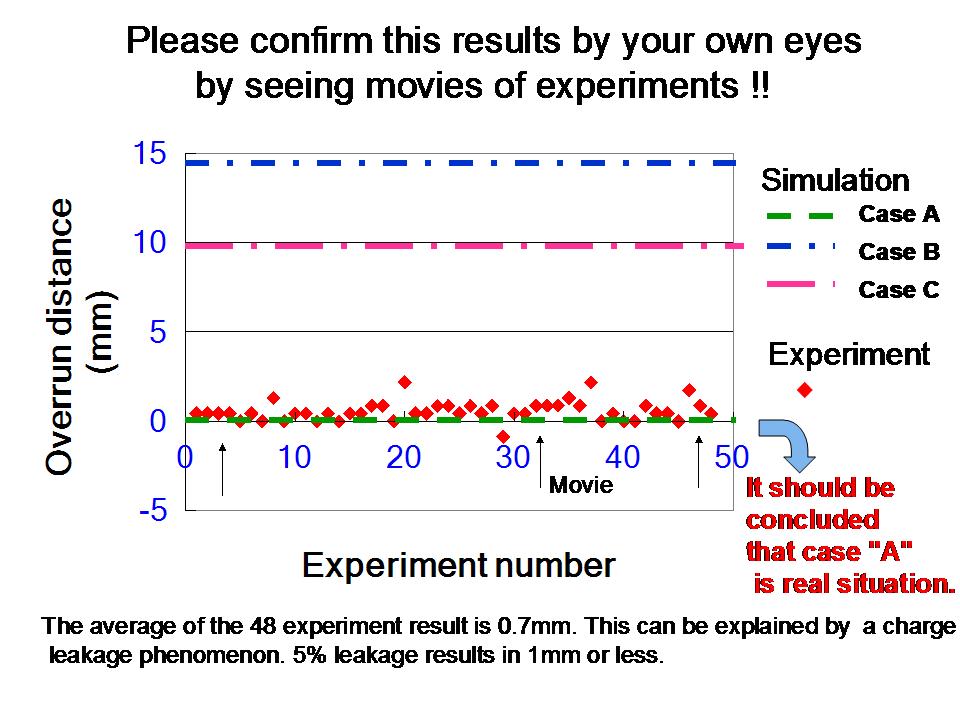
４８回のオーバーラン実測値は、シミュレーションされたケースAの場合のオーバーラン値とほとんど一致することは図３８から明らかです。
これに対して、ケースBとケースCの場合のシミュレーション値は、実測値と大きく異なります。
それゆえ、ケースAが、実際の状態なのだと結論すべきです。すなわち、電界のパターンは、たとえそこを電界に起因する静電力で帯電された導体が動かされても変わらないのです。

私は、ホームページ上で、動画を見せる方法を残念ながら知りません。そこで、この実験の動画を、Uチューブ（http://youtu.be/AWDSqCtAc_k）に置かせてもらいました。

もちろん、実際のオーバーラン距離はゼロではありません。４８回の実験の平均値は0.7mmです。この値は、電荷のリーク現象で説明できます。
導体表面の電荷が時間とともにしだいに大気中にリークしていく現象はよく知られています。そのリーク速度は湿度に依存します。
この実験は低湿環境下で行われました。その時の湿度は 30%RH　でした。これは、電荷のリーク現象を防止するためには完璧な条件ではありません。
もし、往路で５％の電荷が失われたと仮定して、オーバーラン距離を計算すると、1mmかそれ以下になります。この結果は測定された４８回のオーバーラン距離の平均値と一致しています。

図３８:シミュレーションされた３ケースのオーバーラン距離と４８回の実験で計測されたオーバーラン距離

最後に、重大な疑問が残りました。
この帯電された箱型導体は電界より運動エネルギーを得ました。すなわち、電界は、この帯電された箱型導体に運動エネルギーを与えました。
それにもかかわらず電界は変わっていません。それゆえ、箱型導体に与えたエネルギーと等量のエネルギーが。エネルギーを失った電界に補われたはずです。
だれが ?　どのように?
（以下、第三版改訂部分）
電界のエネルギーは、その空間に静止して蓄えられていると考えると、この疑問に答えることができません。
しかしながら、電界のエネルギーは光速度で移動していると考えると、明解に説明できます。奇妙に聞こえるかも知れませんが、量子電気力学ではそのように考えられているようです。

量子力学によれば、素粒子には、クオークとレプトンの２種類があり、前者は、アップ(u)、ダウン(d)、ストレンジ(s)、チャーム(c)、ボトム(b)、トップ(t)で構成されていて、
後者は、電子(e)、ミュー粒子(μ)、タウ粒子(τ)、電子ニュートリノ(ve)、ミューニュートリノ(vμ)、タウニュートリノ(vτ)で構成されています。
さらにこれらを結びつける力を担う素粒子（ゲージボゾン）として光子、ウィークボゾン、グルーオンがあります。
量子電気力学は、光子を媒介とする電子から他の電子に働く力に関する学問です。
量子電気力学は大変難しく私には正確には理解できません。以下は、私の理解できた範囲での個人的な説明です。今後、みなさんのご協力でより正確に書き直したいと思います。
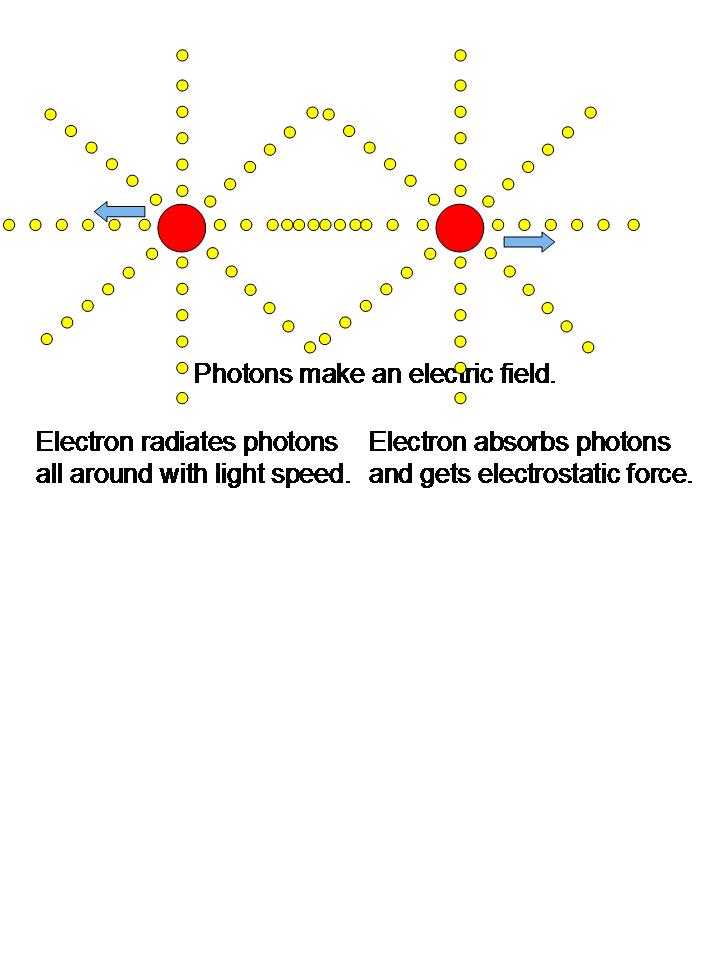
電子は、常時、全方向に、連続的に（仮想）光子を、光速度で放射します。その光子が、他の電子に到達し、吸収された時、静電力が働きます。
すなわち、電界は、光速度で移動する光子で形成されています。それゆえ、電界中のある地点で、帯電体の電子に光子が当たってそのエネルギーが帯電体の運動エネルギーに変換されても、 次の瞬間には後続の光子がそこに到達しているので、また運動エネルギーを与えることができるのです。
すなわち、ある地点で、ある瞬間、電界のエネルギー（光子）が消費されても、瞬時に、後続のエネルギー（光子）が光速度で到達するので、何も変わらなかったように見えるのです。

図３９：電子から放射された光子が他の電子に吸収されて静電力を与える模式図。

"結論"

簡単な実験によって次のことが確認されました。すなわち、電界のある空間が、帯電された導体に一度エネルギーを与えたあとでも、再度同じエネルギーを与えることができる。
この実験の結果は、電界のエネルギーは静的なものではない、いやむしろ動的なものでなければならないことを意味しています。この動的な電界は、電子から放射された光子で説明できます。
エレクトレットで形成される電界のエネルギーのみで駆動される新型静電発電機 [5] が近い将来実現されるでしょう。

"謝辞"

私は、東邦化成�鰍ﾌ、川戸　進、清水　聡両氏に対して、その高電位エレクトレットを試作していただいたご努力に対して心より感謝の意を表します。

"参考文献"

[1] Jearl Walker, Fundamentals of Physics. 8th Edition John Wiley & sons ,Inc. 2008, pp. 671.
[2] Katsuo Sakai, “The electrostatic force that acts on the charged asymmetric conductor in a high electric field,” Proceedings of 2009 Electrostatics Joint Conference (2009) P2.07
[3] Katsuo Sakai, “Electrostatic force that acts on non-sphere shape charged conductors”, Proceedings of 2010 ESA annual Conference (2010) G4
[4] 竹内　薫, 「場」とはなんだろう,　講談社　２０００年 pp. 54.
[5] Katsuo Sakai, Asymmetric Electrostatic Forces and a New Electrostatic Generator, first ed. Nova Science Publish, New York, 2010

　Back to the top of this page.
Back to the top page.