P.Taranzona, "Error thresholds for molecular quasispecies as phase transitions: from simple landscapes to spin-glass models, Physical Review A 45(8) 6038-6050(1992)
・・・Taranzona の論文で、RNAのコピーミス問題をスピン系に置き換えるところは、オリジナルは Little という人が、脳神経系のモデルとして考えたものらしい。(W.A.Little, "The Existence of Persistent States in the Brain", MATHEMATICAL BIOSCIENCES 19,101-120 (1974))
●●●
・・・核酸の種類が2種という単純化をして、N個の核酸が繋がってRNAが出来ているとする。その可能性としては 2^N あることになるから、取り得る状態もそれだけある。これの k 番目を Sk とまとめて表記する。k は 1から2^N である。一つの核酸のコピーが正しく行われる確率を q としている。これが、独立に起こると考えると、1つのRNA が正しくコピーされる確率は q^N ということになる。Sk となる RNA の濃度を xk とする。1回のコピーでこの濃度がどう変わるか、というと、一般的には、
xj = ∑k Wjk xk
とでも表現できるだろう。
X={x1,x2,x3,,,,,} :2N個の成分を持つベクトル
と表記すれば、複製を n 回繰り返した後の X(n) は行列 W を n 回掛けて、
X(n)=WN X(0)
つまり、X(i) が判れば、それに W という行列を掛けて X(i+1) が得られる。この状況に対して統計力学の正準分布モデルを当てはめる。つまり、X(i) という外部変数によって、X(i+1)という平衡状態分布が決まる、と考える。平衡状態は、絶対温度の逆数を β として、 exp(-βEjk) に比例する分布である。このエネルギーE に相当するのは何か、というと、
Wjk=exp(-βEjk)
として逆に決めればよい。一般的には E は簡単な形にならないが、この問題の場合は以下のようになる。
・・・個々の核酸が独立に変異を起こすとする。核酸の状態を sj =±1 とする。j は 1 から Nである。
Sk から Sj への変換において、j=k の場合は最大確率であって、qN となるが、1つだけ核酸が違う場合は (1-q)q(N-1)、2つだけ核酸が違う場合は (1-q)2q(N-2)、という風になるから、何個核酸が違うか、という量があると式が簡単になる。それは Humming Distance dH と呼ばれる。
dH[Sj,Sk]=(1/2){N - ∑i si[j]si[k]}
: i は 1からN、si[k] は Sk における i 番目の核酸(±1)である。
Sj=Sk であれば、dH=0、1つだけ核酸が違っていれば dH=1 となる。全部違っていれば dH=N。
これを使えば、
Wjk = A・ qN・{(1-q)/q}dH[Sj,Sk]
となるが、係数Aは配列Skがミスコピーも含めて何倍のコピーを作れるかという量である。つまりkに依存する。これを replicationlandscapeと呼ぶ。ここで考えるに、更に、作られたRNAのコピーが細胞外に出て、再び他の細胞に感染するのであるか ら、その感染確率の方はjに依存する筈である。これがここには入っていないように思われるが、後で考察する。それはそれとして、
-βE=log(Wjk)=log(A)+Nlog(q)+(1/2){log(1-q)-log(q)}{N - ∑i si[j]si[k]}
=log(A[Sk])+(N/2)log{q(1-q)} +(1/2) log{(1-q)/q}∑i si[j]si[k]}
となって、スピン系との対応で言えば、-β=-(1/2) log{(1-q)/q}がスピン間相互作用/絶対温度に相当し、その前の項は個別の1列スピン状態だけの関数(ポテンシャル項)である。通例 q は 1に近いから、スピンで言えば常磁性となる。ちょっと違うのは、RNA配列に沿った方向での相互作用が無くて、時間軸方向の相互作用しかない、という処である。時間軸方向 に n回これを積み重ねていけば、分子軸方向と時間軸方向という2次元格子におけるハミルトニアン H として、
-βH=(nN/2)log{q(1-q)} + ∑i logA[S(i)] + β∑ij sj(i)sj(i+1)
i=1 からn-1、j=1からN
が得られる。これはあくまでも平衡状態でのスピンの分布という意味だけでこの時間軸方向の端(表面)が RNA変異の動的平衡状態に対応しているのであって、非平衡状態を議論することはできない。一番最初 n=0 は比喩で言えば、固定された初期表面配列ということになる。これに層を積み重ねていけばいずれその表面配列には依存せずバルクの性質として内部の一層の配列分布が得られ る。この RNA系の定常状態はその反対側の自由表面 n回目 における配列分布である。
・・・上式第1項はスピンに依存しないから定数として除外できる。第3項はスピン間相互作用であるが、時間軸方向にしか相互作用が無いのだから一次元 イジング系であり、相転移を起こさない。つまり転移温度は絶対0度(β=∞)となる。第2項が問題である。これは配列軸方向の複雑な相互作用を体現し ているから、この項が入ることによって、相転移を示す可能性が生じる。(例えば、隣接の核酸が同じ時に複製効率が上がる、というような仮定を入れてや れば、配列軸方向には常磁性の相互作用が入り、二次元イジング系の相転移を示すだろう。)Taranzona が仮定したのは Eigen と同じく、特定の配列だけが複製効率を上げる、というモデルである。A0 を特定配列の複製効率で、A1 をそれ以外の全ての配列の複製効率として、A0>A1 としている。この効果をスピンで表現すると、その特定のスピン配列を{ξ1,ξ2,,,ξN}と表現して、
∑i log(A0/A1)・Πj {ξjsj-1}/2
のように表せることになる。掛け算になっているので、1つでも sj≠ξj であれば 0 になるからである。
この表式は自由度 sj について見れば N個の積になっているから、1つの配列層全体 N個のスピン状態が関与する多体相互作用ということになる。
・・・こうして、得られた2次元の格子モデルは Bethe の方法で(数値計算として)解けるようである。Appendix に書いてある。
●●●
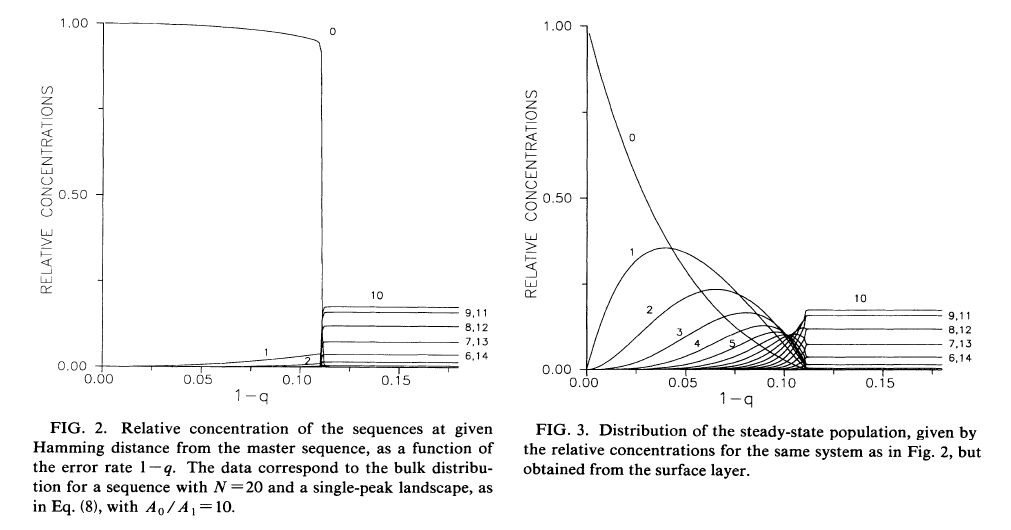
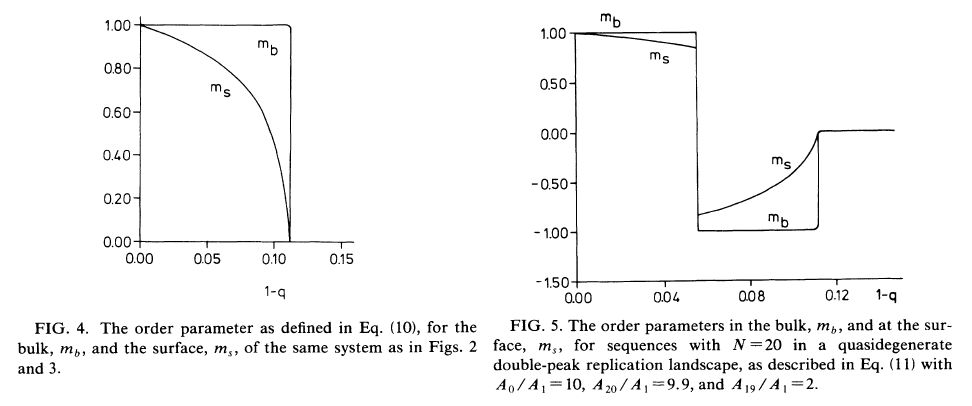
・・・A0/A1 =10, N=20 の場合について、1-q に対する、配列分布依存性が計算されている。Fig.2 と Fig.3 である。Fig.2 はバルクの配列分布であり、Fig.3 は自由表面の配列分布である。いずれも 1-q= 0.11あたりで秩序が失われているので、相転移ということになる。それぞれの曲線は特定の配列からのハミング距離毎に分布が足しあわされているから、ハミング距離を k とすると、均一分布において、N!/{k!(N-k)!} という二項係数×(1/2)^20 となる。バルクの相転移は一次相転移であるが、その自由表面は完全濡れ状態なので、バルクを受動的に反映している。この自由表面が定常状態での核酸の配列分布に対応する。 オーダーパラメータを最適配列からのハミング距離の期待値とすれば(m= (1/N)∑j ξj<xj>)、バルクと自由表面が Fig.4 のようになっている。
●●●
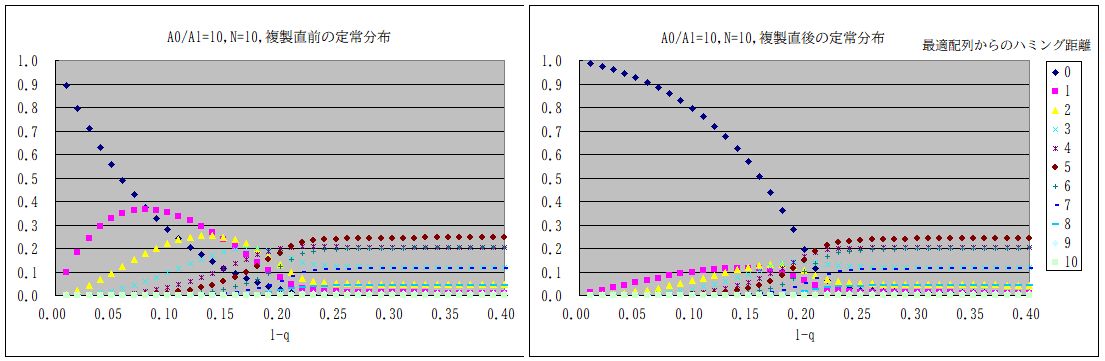
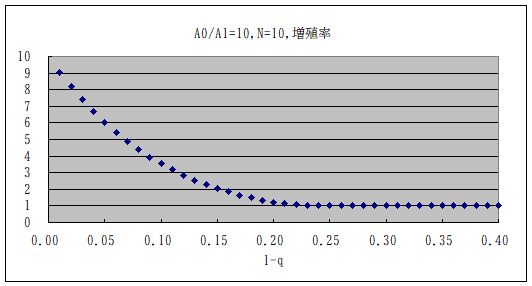
・・・確認の為に、比較的計算が容易な N=10 の場合の Wjk を計算して、初期値を均一分布として、分布が収束するまで掛け算をして計算してみた。下図である。変換行列の固有値も計算してみたが、計算時間はどちらの方法でもあまり変 わらない。この場合にはどうやら (1-q)= 0.21 あたりに相転移がある。RNA の重合度が上がれば、それに反比例してこの閾値が下がるから、ある程度以上長い RNA は複製ミスの為に生き残れなくなることが予想される。これが Eigen の発見であった。ここで、わざわざ計算してみたのは、複製能力自身がどうなるのか、という疑問があったからである。(論文には書かれていない。)通例対角成分が支配的な対 称行列の最大固有値は非対角成分だけが大きくなると少しづつ大きくなる。この最大固有値が複製効率に相当するから、定常状態において複製される RNA 自身は純粋ではなくなるとしても、その複製速度自身は大きくなるのではないか、と思ったからである。しかし、実際に計算してみると、そうではない。コピーミスが増えると、 複製量も小さくなっている。単に非対角成分が大きくなるのではなく、最適配列の対角成分が小さくなるからである。非対角成分が大きくなる効果を上回る という事にすぎない。実際、A1≒ A0・(1-q)N 位になるともはや最適配置の意味がなくなるから、この 1-q が閾値となる。
・・・増殖→複製→増殖→複製→ という繰り返しにおいて、Taranzona は 増幅の直前で見ているから、全体の変換行列 W = 対称行列(複製)×対角行列(増殖)となる(下図左側)。逆に増殖の直前で見れば W = 対角行列(増殖)×対称行列(複製)となる(下図右側)。どちらで見るかによって、当然配列分布は異なる。またこれらを等分して、増殖の中間で見るようにすれば変換行列全 体としては対称となるが、その場合には両者の中間となる。勿論ウイルスの増力率(複製・変換行列の最大固有値)そのものは同じである。実際のウイルス 感染ではどうなのか?ウイルスは細胞の中に入り込み、自らのRNAを複製するのだが、コピーミスはそこで起きる。複製したコピーミスも含めてのRNA が細胞内でウイルスとなり、細胞外に出て、他の細胞に感染する、というプロセスが、増殖である。増幅の直前で分布を見るということは、細胞内での複製 以降のプロセスは変異に依存せず、細胞への侵入確率が A0:A1 で変異に依存するとすれば、細胞に侵入する前のウイルス数を見ていることに近い。そういう意味では Taranzona の採用したやり方は妥当なのかもしれないが、生物学的にはどうなのか判らない。
・・・ということで、デルタ株の遺伝子がコピーミスで自壊していたとすれば、確かに実効再生産数が下がるとは言えるだろう。ただ、具体的に Replication Landscape をモデル化しないと定量的な議論はできない。そこで、簡単の為に複製された遺伝子の中の nsp14 が1回の複製増殖サイクルで割合 p だけづつ壊されていくとする。この nsp14 が壊されたウイルスは壊されなかったウイルスとは別のウイルスではあるが、Replication Lanscape は変わらないとする。ただし、複製ミスの確率 1-q は大きくなっている。元々 q=q0 だったのが、q=q1 になったとする。それぞれの変異種集団における定常状態としての、ウイルス増殖率は上図の一番右側のグラフから判る。これを A(q) とする。nsp14 が壊されると増殖率は A(q0) から A(q1) に変わる。これは細胞の中で APOBEC 酵素によって確率的に起きるから、実質的には A(q0) は複製増殖でほぼ (1-p)A(q0) になる。これが A(q1) より大きければ、nsp14 が壊れてもなお優位ということであるから、ウイルス全体としての増殖率はほぼ (1-p)A(q0)となる。( nsp14 によって増殖率が殆ど 0 に近くなるような場合には、再生産数が 1- p 倍となるだけであって、nsp14 の破壊率も小さい状態で安定化してしまう。)そうでない場合は、ほぼ全部の nsp14 が壊れて、ウイルス全体としての増殖率はA(q1)になる。
・・・q0=0.01(A(q0)=9.04)、q1=0.07(A(q1)= 4.87)を選んで、p を実際に変えて計算した定常状態の結果が下図である。nsp14破壊率というのは q1 という複製ミスを持つウイルスの割合である。これは単なるモデル計算ではあるが、一般的な傾向はこんな感じではないかと思われる。すなわち、実際にどれくらいの割合で nsp14 が壊れているのか、ということ (nsp14破壊率) あるいは1回の増殖サイクルでどれくらいの割合で nsp14 が壊れていくのか(p) と nsp14 が壊れたウイルスと壊れていないウイルスの増殖率比が判れば、APOBEC遺伝子がどれくらい増幅率を下げているのか、が判る。後者の推定が難しいような気がする。但し、 これは体内のプロセスであるから、この細胞感染がが何回も繰り返されて、ウイルスが体外放出され、そのほんの一部が他者の細胞に感染する。増幅率の少 しの違いは体内で何回も繰り返されることでべき乗がかかるので、違いが増幅される。nsp14 破壊率の方は細胞感染が何回も繰り返された後の定常値である。
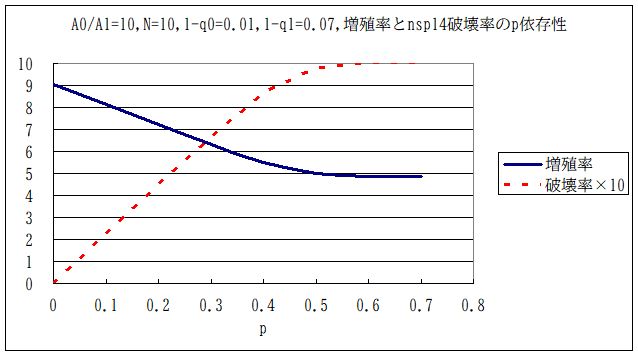
●●●
・・・この論文の主旨は、ここから先にあるが、とりあえずの関心ではないので、簡単に要約だけしておく。Replication Landscape にはいろいろな種類が考えられる。最適配列が一つだけでなく、例えば、丁度裏返しの配列もまた最適である場合、その裏返しの配列がある程度の幅を持っ ている場合には、”相転移”は複雑になる(Fig.5)。もう一つはこういった単純な Landscape ではなくて、もっと連続的なものもあり、その中には神経ネットワークのモデル(Hopfield 型)もある。興味深いのは、Figure 5 のようなケースである。つまり、最も適応した配列ではなくてそれよりも適応度が低くても多数の配列があり、しかもそれらの多数の配列がお互いにある程度のバリアー(峠の高 さ)を持って繋がっている場合には、エラー率が低い場合に最適配列が安定となり(m>0)、中間のエラー率で適応度がそれほどではなくて繋がり あっている配列が安定となり(m<0)、更にエラー率が上がると完全に均一な配列分布になる(m= 0)。この中間的な安定相のバルクはスピングラス相に対応している。スピングラス相は多数の準安定な配列が繋がりあった構造であり、それらの準安定な配列を結ぶのがパーコ レーションである。 パーコレーションが自由に起きている状態は液体であり、それがどれかの準安定配列で凍結すればガラスであり、再安定な配列にまで落ち込めば結晶固体ということになる。