2023.10.11、2024.10.09 追記

『ディープラーニングを支える技術』 岡野原大輔（技術評論社）は何だか受験参考書みたいなスタイルの本である。手っ取り早く概要を掴むには良い。以下その「概要」である。

第１章：人工知能の歴史

1969年：単層ニューラルネットワークの理論的限界（ミンスキー）が指摘されて、しばらくは研究が衰退。

      これはシンボリック派で論理型プログラム言語 PROLOG を使った。さしたる成果無し。理由は以前に解説した。

・・・（注）この頃、ノンシンボリック派も活動していたのだが、人工知能という目的ではなく、脳の認知メカニズムのモデルとして研究していた。福島氏の「ネオコグニトロン」が有名であり、多層ニューラルネットワークの先駆であった。

      →Googleの検索エンジン（Yahooの検索エンジンは人間が分類していた）や 検索連動型広告、AMAZON の推奨システムが成功例。

2006年：機械学習の主流が多層ニューラルネットワークとその学習（ディープラーニング）になる。開発者のジェフリー・ヒントンが名付けた。

2012年に Alex net が画像認識コンテストで優勝して注目された。指導したヒントン教授も驚いた。大学から企業へのインターン学生によって IT企業（Google等）が知る処となった。

多層ニューラルネットワークの概要

神経細胞を模した単純な関数（入力に対して線形出力させて更に非線形関数に代入する）の入力と出力をつないでいって大きなネットワークを作る。（どのようなつなぎ方をするかは経験知である。いくつかのタイプがある。）ネットワークへの入力データを与えて望ましい出力との差異（誤差）を小さくしていくように個々の単純な関数のパラメータ（係数）を変えていく。個々のパラメータ変化による誤差の変化率（勾配）は、ネットワーク構造による依存関係がある為に、出力側に近い方から順に計算すると効率が良い（逆伝搬法）。パラメータもデータも非常に多いので、よく使われる非線形最適化の手法（Marquardt method: 出力をパラメータで微分した感度行列を利用する）は使えない。最も単純な勾配降下法がパラメータを選別しながら使われる。

      人間と比較するとディープラーニングには大量のデータと学習回数が必要であるから、大きな計算リソースを必要とする。

今後の重要な応用分野は構造化されていないデータの分野である。

    論理と知識を計算機上に移し込むエキスパートシステムは、いわば人間が整理した学問・技術体系を人間がプログラムとして計算機に書き込んで、それがユーザーの問題設定に答える、という演繹的なアプローチであるが、機械学習の場合は現実から集めたデータをある程度人間が整理して計算機に与えて、そこからルールや知識を学習させる。つまり帰納的なアプローチである。計算機がどのような形でそのルールや知識を保持しているのかについては、調べれば判るとは言え、必ずしも人間が整理した体系とは一致しない。

    機械学習において、与える学習データと計算機側で用意するルールのパターンが合わない場合には、しばしば過学習が起きる。これは、与えられた学習データの再現性を重視しすぎて、そこから少しだけ外れると全く非現実的な答えを出してしまう状態である。一夜漬け、丸暗記の試験勉強と同じである。ある程度の誤差を許してもよいので、学習データとは異なる課題を与えられても尤もらしい答えをだせるようにすること（汎化能力）が求められる。
（注）実際に計算したことの無い人には判りにくいかもしれないので、一番簡単な例を挙げておく。本当の関数が２次関数 y=x^2 だとして、学習用のデータとして、ノイズも含めて下図の赤◇データ４組を与えて、そこから関数形を推測する問題であるが、パラメータ数２つの１次関数、３つの２次関数、４つの３次関数で最小二乗法でフィッティングした結果を曲線で示している。１次関数では学習用データが再現できていない。３次関数になると学習用データが完全に再現されている。２次関数はその中間である。これを表す学習データに対する平均自乗誤差の平方根が学習誤差である。全体としての予測能力はここでは、x=1,2,3,4,5,6,7,8,9,10 に対してどれくらい予測値が外れるか（汎化誤差）を見ていて、２次関数がもっともすぐれていることが判る。ここでは３次関数が「丸暗記」、過学習である。なお学習データに誤差が無ければ、３次関数ではパラメータが不定となる。つまり、この場合３次関数は誤差に対して過剰に適応しているということである。

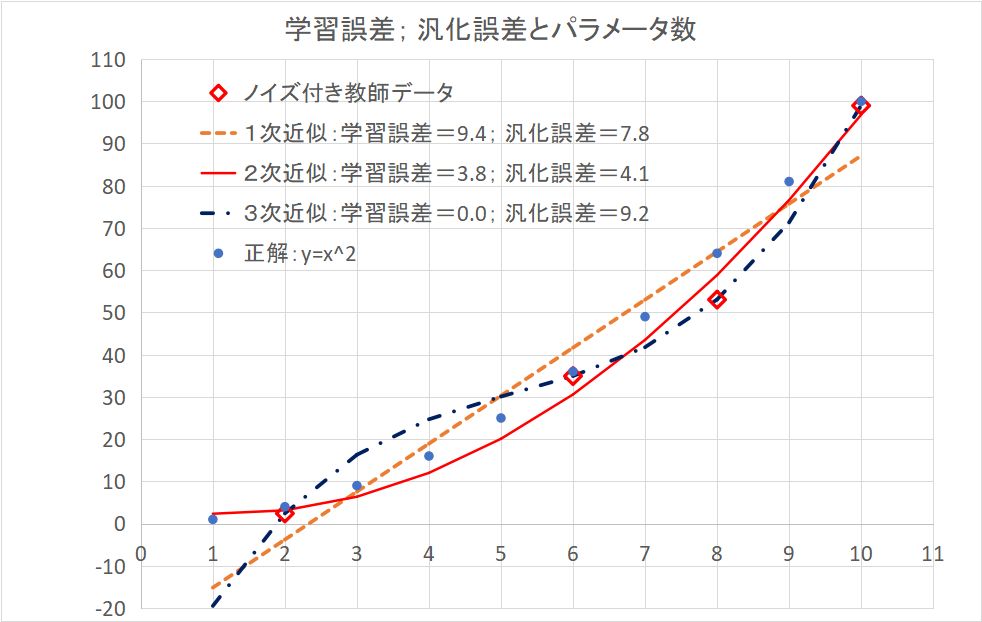
    機械学習というのは、統計解析で言えば、多変量解析に相当する。計算機側で用意するルールのパターンというのはパラメータで表現された各種の関数や分布関数の事である。ディープラーニングではその関数パターンが多層ニューロンネットワークである、というだけのことである。

    学習データは偏りが無くて、出来るだけ多い方が良い。ルールのパターンはそれに見合った自由度でなくてはならない。自由度が高すぎる（何でも表現できてしまう）と過学習になりやすい。ディープラーニングではパラメータ数が非常に多いにもかかわらず過学習が起きにくいのは、ニューロンを模した単位関数が発散的にならないことと、パラメータの最適化が限定されたパラメータを選択しながら原始的な勾配法で行われて、誤差や揺らぎを含むからだと言われている。

●教師あり学習がもっとも容易な学習パターンである。データを与えて、それぞれのデータから導かれるべき模範解答（教師）を与える。その間の誤差を最小化するようにあらかじめ設定された関数系の中でそのパラメータを決める。典型的な例は、x と y の組を沢山与えて、そこから ｙ＝Ax+B というルールを推定する（線形近似）である。与えられたデータに対して模範解答が得られる訳ではないが、その誤差が少ない代わりに、新規データに対してもそれほどおかしな予想はしない。ディープラーニングの例としては、沢山の画像データに対してその分類結果（猫だとか犬だとか）を教師データとして与えて、画像の判別をする、というのがある。

●教師なし学習では、データの特徴を捉えて、最適な表現を求める。多変量解析で言えば、クラスタリング、主成分分析、独立成分分析である。「表現」というのは、データが表現されている次元よりも低い次元でそのデータを近似することである。判りやすい例は、３次元空間に散らばって見えるデータが２次元の曲面に乘っていると近似される場合である。「表現」が得られれば、元々のデータには無いけれどもその表現に沿った新たなデータを生み出すことができる。これが「生成」と呼ばれる。ディープラーニングでの例としては、車の写真をいろいろな角度から撮影した画像を与えて、それらが同じものとして分類されるような「表現」を学習させる。そうするとその表現を利用して、いろいろな角度から見た同一人物を同一人物と判定することが容易になる。また、一つの角度から見た画像から、別の角度からみた画像を「生成」することも容易になる。

●教化学習は教師あり学習と似ているが、データと模範解答の在り方がかなり異なる。ゲームの状況を想定したものである。エージェントが環境に対してとるべき行動（環境を変える）を最適化するのであるが、その基準は将来に亙る環境から得られる報酬の総和である。どのような行動に対してどの程度の報酬（負の場合は罰）をあたえるかを人間が設定することで、エージェントの環境に応じた行動パターンを学習させる。（子供の躾けに褒めたり怒ったりするのと同じである。）報酬は模範解答とは異なり、次元が１、つまり単なるスカラー量である。ゲームの環境（どう行動すればそれくらいの確率でどうなるか）は勿論あらかじめ与えられている。エージェントとしては、直接報酬を得る行動を採るべきかそれとも探索のために試行してみるか、といったジレンマも生じてくる。（これも子供がよくやる。ちょっと怒るかどうか試してみるということ。）
（注）対話型AIでは、学習の最終段階で、非倫理的な内容を出力しないように、ラベラーと呼ばれる人達によって強化学習が行われている。

2.6 機械学習の基本

    この章はちょっと混乱する。例として画像データからその分類を行うのであるが、単純すぎて不自然さを感じる設定になっている。

（注）画素成分を j で表記して、一つの学習データに対してクロスエントロピー損失関数のパラメータ偏微分を計算すると、
      y=1 に対しては、
        ー∂log(q(y=1|x))/∂wj＝xj q(y=0|x)
        ー∂log(q(y=1|x))/∂b＝q(y=0|x)
      y=0 に対しては、
        ー∂log(q(y=0|x))/∂wj＝ーxj q(y=1|x)
        ー∂log(q(y=0|x))/∂b＝ーq(y=1|x)
      つまり、q を計算しておけば、偏微分の計算は簡単である。
（注）実際に４画素の簡単なケースで計算してみた。x も w も 4成分ベクトルとなる。訓練データとしては、x 各成分を 0から 1までの乱数で与えて、教師判断としては、x2 と x3 のいずれもが、x1 と x4 のいずれよりも大きい時に 1、それ以外で 0 という解答を与えた。ただ、この教師判断のアルゴリズムを計算システムは知らない。訓練データセットを下記のように 50セット与えて、上記のモデルに基づいて、パラメータ w と b を、勾配降下法で決めた。結果は (w1,w2,w3,w4,b)＝(-16.221, 10.922, 26.975, -10.096, -12.702) となった。確かに教師のアルゴリズムをある程度理解したようなパラメータ値になっている。つまり、score＝w1x1+w2x2+w3x3+w4x4+b は、x2 や x3 が x1 や x4 に比べて大きい時に大きくなるのだが、元々の教師アルゴリズムではない。下記に示すように、具体的に教師データから計算された予測値としては、不正解のものが 1つ含まれていた。これはまあ、教師アルゴリズムに対して、モデルがあまりにも単純なためであろう。（なお、教師解を x2+x3＞x1+x4 の時に 1、それ以外で 0 という風に与えると、完全学習となる。）
        x1           x2            x3           x4        q(y=1|x;Θ) 予測値   教師判断
       0.503       0.705       0.986       0.130       1.000         1         1
       0.384       0.071       0.068       0.680       0.000         0         0
       0.025       0.726       0.547       0.087       1.000         1         1
       0.640       0.805       0.551       0.441       0.020         0         0
       0.407       0.279       0.566       0.318       0.015         0         0
       0.498       0.512       0.791       0.210       0.982         1         1
       0.924       0.852       0.200       0.816       0.000         0         0
       0.330       0.120       0.412       0.874       0.000         0         0
       0.664       0.780       0.180       0.547       0.000         0         0
       0.173       0.005       0.720       0.667       0.059         0         0
       0.038       0.613       0.169       0.569       0.000         0         0
       0.212       0.454       0.543       0.968       0.002         0         0
       0.791       0.955       0.476       0.776       0.000         0         0
       0.152       0.633       0.086       0.560       0.000         0         0
       0.960       0.823       0.065       0.807       0.000         0         0
       0.157       0.662       0.941       0.506       1.000         1         1
       0.679       0.408       0.652       0.006       0.150         0         0
       0.703       0.935       0.162       0.550       0.000         0         0
       0.837       0.897       0.610       0.108       0.248         0         0
       0.615       0.063       0.330       0.328       0.000         0         0
       0.248       0.989       0.976       0.787       1.000         1         1
       0.415       0.523       0.163       0.906       0.000         0         0
       0.802       0.793       0.344       0.908       0.000         0         0
       0.529       0.836       0.456       0.191       0.145         0         0
       0.414       0.728       0.712       0.281       0.993         1         1
       0.200       0.615       0.659       0.851       0.488         0         0
       0.037       0.734       0.951       0.096       1.000         1         1
       0.731       0.101       0.245       0.342       0.000         0         0
       0.468       0.880       0.436       0.878       0.000         0         0
       0.521       0.978       0.654       0.529       0.862         1         1
       0.657       0.820       0.927       0.301       0.999         1         1
       0.945       0.308       0.886       0.592       0.001         0         0
       0.978       0.071       0.921       0.089       0.021         0         0
       0.968       0.698       0.600       0.132       0.003         0         0
       0.342       0.631       0.029       0.404       0.000         0         0
       0.541       0.377       0.299       0.327       0.000         0         0
       0.504       0.622       0.693       0.581       0.222         0         1
       0.163       0.106       0.101       0.477       0.000         0         0
       0.825       0.268       0.423       0.306       0.000         0         0
       0.820       0.083       0.674       0.671       0.000         0         0
       0.863       0.371       0.605       0.114       0.001         0         0
       0.903       0.160       0.959       0.437       0.015         0         0
       0.063       0.504       0.383       0.720       0.006         0         0
       0.473       0.837       0.147       0.913       0.000         0         0
       0.277       0.553       0.462       0.034       0.727         1         1
       0.071       0.921       0.628       0.611       0.999         1         1
       0.671       0.310       0.756       0.459       0.012         0         0
       0.429       0.942       0.463       0.854       0.004         0         0
       0.223       0.718       0.252       0.719       0.000         0         0
       0.073       0.920       0.035       0.035       0.037         0         0

・・確率的勾配降下法の話は省略：訓練関数はパラメータ空間上のスカラー関数になっているので、現在のパラメータ値での値から一番少ない距離で値が下がる方向を見つけて少しづつパラメータを変えていくこと。

      クロスエントロピー損失関数を使った機械学習は最適な確率分布を求める最尤法と同じである。
      更に、正規化の項はベイズ推定における事前確率分布と同じである。事後確率最大化（MAP）と呼ぶ。

第３章 ディープラーニングの技術基礎

      このような特徴量を人間が与えるのではなく、データから学習するのがディープラーニングの特長。

      実装・物理レベル    神経細胞のネットワークーーー単純な非線形関数のネットワーク

・・f(wx＋b) ： f(x) は非線形（活性化関数）w,x,b はベクトル： これを３層にすると万能近似関数ができる。

        このニューロンの軸索出力（活性値）が f(w1x1+w2x2+w3x3++++b) となる。

・・多層ニューラルネットは冗長性（多表現性）を持つ（同じ関数に対して多数のパラメータセットがある）。

・・層の構成、層間でのパラメータ共有、等あらかじめ事前知識（帰納バイアス）を入れることが多い。

          目的関数は、教師あり学習では「訓練誤差」、生成モデルでは「対数尤度」、強化学習では「報酬」、「予測誤差」

・・接続層のいろいろ（種々の用途に応じている）

●総接続層：層の全てのニューロンの出力が繋がった層の全てのニューロンの入力となる。基本形である。
   活性化関数が線形のもの（linear layer）が基本系であるが、非線形のものが

●多層パーセプトロン（MLP）と呼ばれている。

●プーリング層：層内の一部分の最大値や平均値を出力するようにパラメータを固定する。

              ノイズ除去や自由度の制限ができて収束しやすくなる。

● ゲート機構
              回帰結合を改良するために別途セル状態を作っておき、記憶量を調整する。
              記憶というのは、時間的に離れた状態に影響を及ぼすという意味である。
              ある時刻のニューロン層の状態をある割合で忘れていくことで、記憶を制御する。
              LSTM （Long short-term memory）と GRU （Recurrent gate unit）がある。

      他多数。。。ベクトル的なものもある。

    2010年頃までは、ディープラーニングが上手くいくときもあったが、失敗することが多かった。ディープラーニングの成功は単に計算機の能力向上だけによるものではない。開発者の現場的な発想と試行錯誤に負う処が大きい。何故うまくいったのか？は判らないままに成果が挙がって、その理由が後から判ることが殆どである。

・・活性化関数として、当初はシグモイド関数が使われていたが、ReLU を使うとうまくいった。これは、誤差をきちんと層間に伝達出来て（勾配消失が起きにくく）、適度な非線形性を持つ関数だったからである。

4.2 正規化層

・・それだけではなく、正規化層の導入によって、非線形性が保証された。これは、活性化関数に代入する前の直接出力（wx＋b）を正規化（平均値を引き算して、標準偏差で割り算）する層である。学習データ x が大きすぎたり小さすぎるとその間に 0 を含まなくなって線形則に乗ってしまう。正規化によって非線形性を保証だけでなく、勾配ベクトルの方向が多様になって収束が速くなり、フラットな解（周辺の解も最適に近い）が得られるので汎化性能も得られるという理屈が判ってきた。

（注）活性化関数 f として ReLU を使った場合、wx+b＞0 の場合、∂f/∂w＝x、∂f/∂b＝1 となるが、wx+b≦0 では偏微分が 0 になる。wx+b がうまくばらけた学習データであればよいので、偏らないように正規化するということ。

・・バッチ正規化では、訓練データ全てについて正規化する。ただこうするとパラメータ更新の度に各層の活性値正規化をやり直さねばならないので、計算量が増える。確率的勾配降下法で選択したパラメータの範囲に限定する。

・・最適なパラメータは必ずしも正規化されたものではないので、どの程度の正規化をするのか、というパラメータも入れておいて、同時に最適化する。これは、元のデータの情報を出来るだけ保存するのか、それとも重要な情報に限定するのか、という選択を自動的に行う、という機能を持っていることが判った。入力側の層は前者で出力側の層は後者である。

・・正規化に使う統計量は訓練データでしか得られないから、推論時には使えない。そこで訓練時の統計量を保持しておいて推論時に適用する。

・・バッチ正則化の最大の利点は目的関数の最小値近傍が歪みの少ない盆地状になることであることが判った。これによって勾配降下法の収束性が劇的に改善されたのである。

・・バッチ正規化が難しい場合のやり方として、層正規化、サンプル正規化、グループ正規化がある。要は一部の活性値に限定して正規化することである。

・・重み正規化は 重みパラメータ w を正規化する方法。

・・より高度な正規化として白色化がある。これはデータ間に含まれる相関を取り除くように変換することで、目的関数の等高線が円になるように変換する。相関から共分散行列を得て、固有値で規格化する。（普通の非線形最適化でも同じようなことをしている。）

・・通例 h1= f(w・x0+b) を次の層の x1（入力）に使い、h2＝f(w・h1+b) とすべきところを、
      h2＝h1＋f(w・h1+b) とする。（w や b は各層で異なる。） Residual Network と呼ぶ。
      これを使わないと、勾配の掛け算によって誤差伝搬が消えてしまい、10層位が計算の限度になってしまう。
      勾配の伝搬に ∂h2/∂h1 が掛かっていくのであるが、この項に 1 が追加されていることになる。
      元の情報を縮約して次の層に送るボトルネックというやり方をしても、元の情報の一部が伝わる。

      いろいろな変種があるようであるが、省略。

（ここまでの感想）
・・多層ニューラルネットワークというのは、元々は脳のモデルとして考えられていたので、学習方法もヘッブの法則を使っていたのだが、これを単なる多変数の非線形関数と見なして、データを再現するようにパラメータ最適化をすると考え直した。そこで、並行して発展していた数値解析における機械学習の方法が応用された。その効率化には一般的なニューラルネットワークではなく、層を成して結合しているタイプのものに特有の計算方法、バックプロパゲーションが決定的な役割を果たした。その方法に特有のいくつかの困難（微分が微小になってしまうとか）が付け焼刃のような方法で荒っぽく修正された。しかし、実際にやってみると開発者も驚くほどの高性能を発揮した。これが転機となった。
・・科学者的な見方をすれば、複雑な現象の背後には何か原理的な法則が潜んでいて、そのプラトンのイデアのようなものを見つけることで、現象が再現出来たり、その背後にある意味を知ることができる、と考えられるのであるが、多層ニューラルネットワークで学習される多数のパラメータ値の組をいくら眺めても法則（意味）は見えてこない。そもそも、そういう解は非常に多くあって、どれでも良いのである。

4.4 注意機構

        が注意機構によって使えるようになる。

     １．の内部状態というのは各ニューロンの活性化値であり、「現在」である。ニューロンの数しか自由度はないが、２．の重みはニューロン間の接続数であるために圧倒的に自由度が高い。これは長期記憶となる。更に、重みの学習に対して、時間的な忘却機構を入れておけば、これが短期記憶に相当する。Fast Weight という。

・・３．の注意機構は、過去のデータや別のシステムからの出力等を取り込むことができるが、更に自己注意機構（Transformer）というのは、前の層を注意対象として、次の層でまとめて処理する。具体的にどうやるのか？の説明はさっぱり判らない。。。別途じっくりと勉強した方が良さそうである。多分ゲート機構をもっと自由にしたものなのだろう。現在の多層ニューラルネットワークの実際上の応用、画像認識や言語モデル等では必須であり、今後も最も重要な技術分野であるという。

（感想）現実世界に対処するためには、おそらく単純なニューラルネットワークによる情報処理では間に合わないのだろうと思う。課題を判断し（分類し）その分類に沿って過去の処理結果を参照する、といった分岐的なやり方が必要になる。概念的には一つ上の階層での判断が必要なのだが、それも学習させるわけなので、そのための新たなパラメータを持つニューロンを介在させておく、ということになる。そのパラメータもまた「学習」させるのである。。。

（注：2024.10.09）    ノーベル物理学賞が、ホップフィールドとヒントンに与えられた。ヒントンは当然だろうが、ホップフィールドはちょっと方向が違うんじゃないかなあ、と思ったが、まあ相補的なのかもしれない。「基礎」を重んじるノーベル賞らしい。現在の第３世代 AI の原点は理論物性物理屋さんの遊び心から生まれた、という見方をしている、ということになる。

    1982年に発表されたホップフィールドネットワークというのは、物性物理のイジングモデルの拡張版ともいえるが、相転移の説明のためのイジングモデルとは違って、全てのスピンがお互いに繋がっている。勿論そもそも目的が違う。

    多数の学習用目的パターンをスピン分布で与えておいて、スピン間相互作用パラメータをそのスピン分布においてエネルギーが最低になるように決めていくのであるが、決められたパラメータ値はスピン分布毎に異なるので、それらのパラメータ値を平均化してしまう。これが学習である。つまり、学習は数式で書けば一つの式の計算で終わる。

    実際にパターン判別に使う時には、いろいろなノイズを含んだスピン分布を与えておいて、そのスピン分布をすこしづつ変えていってエネルギーを最小化すると、ノイズの取り除かれたパターンが再現される。つまり、神経細胞同士の結合の度合いの分布によって、神経細胞の興奮パターンが「記憶」されていることになるから、「連想記憶」のモデルとして解釈できる。（関係的存在論のモデルとも言えるか？）

    エネルギーランドスケープ（パラメータ空間におけるエネルギー分布）が沢山の極小値を持っていて、それぞれが記憶されたパターンであり、与えられたノイズを含むパターンがどの極小値に近いか、ということでパターンを判別する、ということであるので判りやすい。

    これに物性論の真似をして「温度」を導入したのが、「ボルツマンマシン」である。物性論で使われるモンテカルロシミュレーションと同じやり方でパターンの遷移確率を与える。ただし、温度は単なる収束の為の手段にすぎない。収束させるときに最初は温度を高くしておいて、いろいろなパターンを試しやすくして、最終的には温度を低くして最低エネルギーのパターンを見つける。

    これらは、単層の内部で総ての神経細胞が結合しているというモデルなので、層内に結合が無くて層間に結合がある、という多層ニューラルネットワークとは対照的な構造をもっている。言い換えれば、多層ニューラルネットワークの欠点を補うという側面を持っているともいえるだろう。実際、transformer という機構がそういう風に解釈されているらしいが、よくは判らない。

      画像分類、音声認識、自然言語処理 が説明されている。

    画像データは、何番目の画像か n、何番目の色成分か c、縦横位置のどこか (h,w) の４つで指定されるテンソル X[n,c,h,w] として扱われる。例えば、X[7,2,45,30]=0.5 の意味は、7番目に与えた画像の、高さ位置=45、幅位置=30という画素における緑色成分の値が 0.5 である、ということ。これが入力で、出力はその画像が何か（分類）ということである。

    (h,w) が圧倒的に大きな次元を持つから、これを少しづつ要約して小さな次元にして、その代わりに その要約パターン番号として c の次元を増やしていく。c は色だけでなく、画像要素（線分とか円とか、、、）を意味することになるので、チャンネルという用語が充てられている。これを繰り返して、画素が 1 になって、チャンネル数が非常に多くなると、そのチャンネルが「何か」を表すことになる。基本的には畳み込み層とプーリング層でこれらの変換を行う。最後に判別にあたってはチャンネルデータベクトルを正規化して、もっとも大きな成分（例えば「中島みゆきの顔」とか）を回答する。

    （注）簡単な例を考えてみる。２値画像（白黒だけ）を考える。その中で５×５の正方形画像だけを見ていろいろな方向に傾いた直線があるかどうかを判別して、その直線の種類（例えば縦横斜めの４種類）をチャンネルとする。この操作を元画像内で正方形の位置をずらしながら行って、次の層のデータとする（これが畳み込み層である）。これではチャンネル数が４倍に増えただけなので、畳み込み層内において、ある程度の範囲での平均化操作を行って解像度を減らして、画素数を1/4 に落とす（これがプーリング層である）。その次に縦横斜めの線が隣り合う画素間でうまくつながっているかどうかを畳み込み層で判定していくと、特定のパターンの線画を見つけることができる。どんな種類の画素パターンを見つけるかは畳み込み層における重みパラメータが決めるので、それを学習させることになる。設計者が決めるのはあくまでもいろいろな層の繋がり方（スキーム）である。

RGB の３チャンネルで、224×224画素の画像が入力である。それに11×11画素をカーネルとする畳み込み層とプーリング層をつないで行って、13×13画素で192チャンネルのデータまで圧縮する。その後、画素数を変えずに畳み込み層を３回繰り返す。これを１画素2048チャンネルの画像にしてから、総結合層を２回通すことでほぼ分類が終わる。これを1000チャンネルまで平均化して出力データを正規化して各チャンネルの予想確率とする。総結合層に至るまでの計算は多数の GPU を並列で通すことで高速化している。

● VGGNet は2013年のコンテスト２位で、カーネルサイズを 3×3 と小さくする代わりに、畳み込み層を３倍位に増やした。

● GoogleNet も2013年のコンテスト１位で、その特徴は カーネルサイズをいろいろと用意しておいて、それらを並列させながら組み合わせているところである。モジュール名を Inception という。拾い出すべきパターンのサイズの多様性に対応したものである。

● ResNet は2015年のコンテスト１位で、スキップ接続を導入して層数を一気に152まで増やして成功した。

● SENet は2017年のコンテスト１位で、注意機構を導入して成功した最初の画像認識システムである。Squeeze 操作というのは、画像からいろいろな特徴を捉えたチャンネルを集約して、この画像ではどの特徴が支配的なのかを選別する。次にExcitation 操作は、その選別された特長（特定のチャンネル）以外の情報を消してしまう。これがつまり注意機構ということである。

    以上は画像処理の為に考えられたとも言える畳み込み層を使ったやり方であったが、別途言語処理で使われるようになった Transformer と普通の全結合多層ニューラルネットとの組み合わせでも同等の性能が得られることが判ってきた。

    音声信号を受け取って、それを文字列に直して出力する。最初にスペクトログラム（短時間内でのフーリエ解析を時間をずらしながら行って、時間軸上に周波数成分を並べる）を作り、フィルターで高周波を落として、周波数が高くなるにつれてサンプリング数を落とす（聴覚の特性らしい）。

    ここから、スペクトログラムの特徴分析を行って、「音素」に変換する（音響モデル）。入力は各周波数成分値であるが、時系列データとなっている。これをより疎な時系列の音素成分値データに変換する。ただ、音素の特徴は会話の中の状況によって微妙に変わるために、難しくなるらしい。音素の連なりが判れば、「文字列」が判る。

（疑問）スペクトログラムの特徴と音素との関係や、音素と文字との関係は、よく研究されているので、あらかじめ与えておくのだろうか？それともそれも学習するのだろうか？

    次に、言語モデル（文字出現の時系列相関）を適用して、得られた文字列がどれくらい尤もらしいかを判定して、話されていた文字列を推定する（言語モデル）。

    最初に音響モデルの段階で多層ニューラルネットワーク（再帰型 RNN、畳み込み型 CNN）が導入されたが、最近は言語モデルにも多層ニューラルネットワークが使われるようになった。

    音響モデルの出力は空白も含めた候補文字列の確率分布の時系列であって、確定した文字列ではない。それらの候補を空白を無視して繋いでいったときに、どれくらい教師解の文字列と一致するかを判断して学習する。

    Speller では、

まず AttentionContext を使って、背景ベクトル ci を求める。

    現在時刻の情報 si と過去の時刻の情報 hu を入力としてそれぞれ総結合ニューラルネットワークを使い、これらの内積から、過去の情報の内でどれを重視するかを決める。これで重みを付けて足し合わせて背景ベクトル ci を得る。つまり学習するのは、データ系列のパターンに応じた過去データの重要度ということである。

    得られた背景ベクトル(c(i-1)と、直前に生成した文字列 y(i-1)と直線の状態 s(i-1) から再帰結合（RNN）によって、次の状態を求める
           s(i)＝RNN(s(i-1),y(i-1),c(i-1))。

    状態と背景ベクトルから、次の文字の確率分布を求める。

    学習データに正解の系列だけを使うと、その周辺でしか最適化されないので、推論から推定された文字列も学習データの一部に入れるようにしている。

    最後に実際に使う場面（推論）においては、学習済みのネットワークからの出力を使うのであるが、それは過去の文字列条件付き確率分布としてしか与えられていないので、そこから最もありそうな全体としての文字列の確率分布を求める必要がある。一つの時刻の確率が離れた過去の時刻の確率に依存している為に動的計画法が使えない。ビーム探索法というのが使われるらしい。（どちらもよく判らないが。。）数学的保証は無いが経験的にはうまく行くということである。更に適切な言語モデル（文字列の出現確率分布表）を利用して候補を絞り込む、ということで、言語モデルが必要になるらしい。

    自然言語処理にはいろいろなタスクがあるが、ここでは一番簡単な言語理解に限定する。

    大規模テキストデータ（corpus）を使って事前学習する。単なる単語の並びから文や段落のまとまりを見つけるという課題を与えて学習させる。文字や単語はお互いに何らかの相関があるので、それをうまく表現するような多次元空間を作り、その中の点として要素を表現する。これを「埋め込みベクトル」という。多変量解析でよく使われる考え方であるがここではその結果を入力に使う。Word2vec とか Glove という手法が知られている。ベクトルとして表現されれば、多層ニューラルネットワークへの入力ができる。更に、単語列から次の単語を予測するモデルを学習させる。

    大きな成功を収めた最初の言語表現学習が BERT（Bidirectonal encoder representation from transformers）である。BERT の学習方法は、文の一部の単語をマスクして与えて、その単語を予測させるというやり方である。国語や社会科の試験問題と同じく、ネットワークはこの学習によって、単語の連なりから何らかの状況理解をしていることになる。ただし、マスクした正解の文だけで学習させると、マスクしない文の意味理解に支障をきたすことが知られてきて、マスクした一部の単語に正解を入れてみたり、違う単語を入れてみたりして、学習方法を改良している。このBERTから最終段階の単語予測部分を取り除けば、それが文の理解の部分となるので、（ただし、その「理解」を語ることはできない）いろいろなタスクの為のネットワークを追加して学習させることで、いろいろなタスクのシステムができる。例えば応答文を出力させれば、会話システムとなる。

    BERT のスキームの要点は自己注意機構（Transformer）である。経時的に離れた位置の情報を使うことができる。通常の言語モデルが単語列から次の単語を予測する（確率を与える）いわば生成モデルであるのに対して、BERTはマスク単語を予測するモデルなので、時系列の過去と未来の両方の情報を利用していることになる。大量のコーパスを使った学習には大きな計算負荷が伴うが、それが可能になってきたという事情もあって、BERTが成功した。

    結局自己注意機構の中身は判らないままで終わった。これは別の資料で勉強するしかないだろうが、感想的にいうと下記のように思われる。

画像理解の場合は入力データに時間軸が無いから比較的判りやすいのであるが、音声解析や言語解析になると、経時データを扱うことになる。しかし、経時データとは言っても時間軸上に並べてしまえば、新たな空間軸と同じ事なのである。力学的世界観に染まっていると、ついつい時間的な前後関係には因果関係が潜んでいると思ってしまうものだから、混乱するのである。人間が言葉を発する時、msec 単位の短い時間内においては喉や口腔の物理的生理的構造に由来する因果関係が反映されるのであるが、それはいわばデータに対する拘束条件にすぎない。つまり、人体の構造上発生する音はある程度の範囲に収まっていて、母音は直前の子音に影響されるとか、そういう因果関係があるにすぎない。それ以上の時間で展開するデータは脳の言語中枢で指令された一連の音声であって、因果関係という意味では、一連の音声内部には因果関係は無くて、全体が結果であり、原因は脳の方にある。BERT の成功は、文章データ内の時間的前後関係を等価に扱ったことにある。（学習の設定が文章内の任意の場所の単語予測課題であったから。）文字や単語がそこに置かれている原因は文章の前後関係で言えば前にも後ろにも等価にあって、しかもその因果関係は前後で異なる。このような事情は時間軸というものが空間軸の一つのようでありながらも画像解析のように全く等方的な空間軸とは異なることを示している。だから単純な畳み込み層で扱うことが出来ない。だからと言って全結合層で扱えば計算量が発散する。文法構造を学習するような仕組みが必要なのである。それは結局単語を同定した後で、その単語が要求する時間的に前後する他の単語をうまく見つける仕組みである。要求するということは結合の係数が変わるということであって、そもそも学習済みのネットワークでは結合の係数（w と b）が学習されて決まっているのであるから、無理な話になる。つまり、単語に応じて結合係数を実質的に変える仕組みが必要になる。それは付随する別のネットワークに任せるしかない。単語に対して別の単語の位置を探索するように重みが学習されて、その重みが結合係数に掛け算でかかるような仕組みになる。一つ上の階層のネットワークとも言える。これが「自己注意機構」なのであろう。それはある意味で、時間軸上離れた過去と未来の状態を記憶しておいて再利用することでもあるが、脳における記憶はあくまで過去の記憶であるから、ちょっと違う。

10.14
貸し出し延長をしたら、続編（２）があることに気づいた。やはり好評だったのだろう。こちらも貸し出し予約をしておいた。
ディープラーニングを支える技術
    「正解」を導くメカニズム〈技術基礎〉
ディープラーニングを支える技術（２）
    ニューラルネットワーク最大の謎