3.13.1 丸め誤差
数値演算で注意を要するのは丸めの誤差(round-off error)です。これは、数値が すべて有限の桁数の範囲内で扱われるために、有効桁の最下位より1つ下の桁で四捨五 入(つまり2進数で0捨1入)されることによるために起こる計算誤差です。丸め誤差 でとくに注意が必要なのは、浮動小数点数の加算と減算です。 大きな数と小さな数の加算では、小さい方の数値が結果に反映されれないという情報 落ちという現象が生じます。この様な誤差を積み残しといいます。また、同じ程度の 大きさ同士の引き算で、有効桁数が減少する桁落ちという現象が起こります。 以下では、この様な丸め誤差による計算誤差について考察します。
3.13.2 「0.6 - 0.4」 は 「0.2」 ではない !?
2つの正方行列の積(および順序を交換した積)が単位行列になるとき。これらは、 互いに逆行列の関係にあります。例えば次の2つの行列は互いに逆行列です。
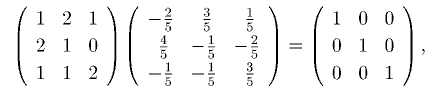
ところが、この簡単な行列の掛け算をプログラムで実行すると結果は単位行列になりま せん。
// lst03_31.cpp
// 計算誤差
#include <iostream.h>
#include <iomanip.h>
int main()
{
// 行列
double a[3][3] = {{ 1.0, 2.0, 1.0},
{ 2.0, 1.0, 0.0},
{ 1.0, 1.0, 2.0}};
// 逆行列
double b[3][3] = {{ -0.4, 0.6, 0.2},
{ 0.8, -0.2, -0.4},
{ -0.2, -0.2, 0.6}};
// 行列の積
double c[3][3];
double sum;
int i,j,k;
for(i = 0; i < 3; i++)
for(j = 0; j < 3; j++){
sum = 0.0;
for(k = 0; k < 3; k++)
sum += a[i][k] * b[k][j];
c[i][j]= sum;
}
// 結果の出力
cout << "行列と逆行列の積:" << endl;
for(i = 0; i < 3; i++){
for(j = 0; j < 3; j++)
cout << setw(15) << c[i][j];
cout << endl;
}
cout << endl << "第1行2列要素の計算:" << endl;
sum = 0.0;
for(k = 0; k < 3; k++){
cout << setw(5) << sum << " + (";
double d = a[0][k] * b[k][1];
cout << setw(5) << d << ") = ";
sum += d;
cout << setw(15) << sum << endl;
}
return 0;
}
|
[実行結果] ソースプログラム ( lst03_31.cpp ) |
行列と逆行列の積:
1 -5.55112e-17 -1.11022e-16
0 1 0
0 -5.55112e-17 1
第1行2列要素の計算:
0 + ( 0.6) = 0.6
0.6 + ( -0.4) = 0.2
0.2 + ( -0.2) = -5.55112e-17 |
この様に、非対角要素のいくつかは0にはならないで、微小な値になります。状況から これらの値はゼロであることは分かりますが、この様な簡単な計算で誤差は生じます。 実行結果に示すように、例えば第1行2列目の要素は 0.6 - 0.4 - 0.2 = 0.2 - 0.2 という計算を行っていて、この引き算に誤差が含まれています。このときの浮動小数点 数の値の内部表現を見てみましょう。 「#1変数を覗いてみよう (6)」で作成した double.cpp 内の関数 dec2bin() を使 ってdouble型データのビットパターンを表示すると次のようになっています。
0.6 - 0.4 の内部表現(double型) [指数部 ][ ---- 仮数部 ----- ] 00111111 11001001 10011001 10011001 10011001 10011001 10011001 10011000 0.2 の内部表現(double型) [指数部 ][ ---- 仮数部 ----- ] 00111111 11001001 10011001 10011001 10011001 10011001 10011001 10011010 0.6 - 0.4 - 0.2 の内部表現(double型) [指数部 ][ ---- 仮数部 ----- ] 10111100 10010000 00000000 00000000 00000000 00000000 00000000 00000000 = -1.000000×2^-54 = -5.55112e-17 |
つまり「0.6 - 0.4」と「0.2」とでは、仮数部の下位ビット2桁(右側)の値が違って います。この差が、「0.2 - 0.2 = -5.55112e-17」という結果になったわけです。
3.13.3 なぜ桁落ちするのか
どのように計算誤差が生じるのか、紙の上の計算で追跡してみましょう。まず引き算さ れる実数値 0.2 は正確な値ではなくて丸め誤差を伴います。 0.2 を2進数で表すと、 0.2の2進数表現 = 0.001100110011............. , と循環小数になります。これをIEEE標準形式で表すと、最初に1が現れるケタの次のとこ ろへ小数点を動かして、 1.1001100011001100....... ×2^−3 , というビット並びになります。double型では小数点以下の部分(仮数部)を52ビットで 表すので、次の桁53ビット目を丸めて(0捨1入)、 ....10011010 で終わります。 この丸めを行うための1つ下の桁のことを保護桁と呼びます。 次に、「0.6 - 0.4」を検討します。実数値 0.6 と 0.4 の内部表現は次のようになっ ています。
C:\Source> double 実数値を入力して下さい: 0.6 double型の入力データの内部表現(2進数表示) [指数部 ][ ---- 仮数部 ----- ] 00111111 11100011 00110011 00110011 00110011 00110011 00110011 00110011 入力データ: 0.600000 = 1.200000×2^-1 C:\Source> double 実数値を入力して下さい: 0.4 double型の入力データの内部表現(2進数表示) [指数部 ][ ---- 仮数部 ----- ] 00111111 11011001 10011001 10011001 10011001 10011001 10011001 10011010 入力データ: 0.400000 = 1.600000×2^-2 |
これらも循環小数であって、 下位ビットが丸められています。0.6は切り捨て、0.4は切
り上げです。
引き算「0.6 - 0.4」を紙の上で再現してみましょう。
(0)元の数値(仮数部は小数点以下の値で、整数1が省略されていることに注意)
0.6 = 1.0011 00110011 00110011 00110011 00110011 00110011 00110011 ×2^-1
0.4 = 1.1001 10011001 10011001 10011001 10011001 10011001 10011010 ×2^-2
(1)保護桁の付加(下位ビットに1桁0を追加)
0.6 = 1.0011 00110011 00110011 00110011 00110011 00110011 00110011 0 ×2^-1
0.4 = 1.1001 10011001 10011001 10011001 10011001 10011001 10011010 0 ×2^-2
(2)桁をそろえる(指数部の小さい方の数値を1桁右シフト)
0.6 = 1.0011 00110011 00110011 00110011 00110011 00110011 00110011 0 ×2^-1
0.4 = 0.1100 11001100 11001100 11001100 11001100 11001100 11001101 0 ×2^-1
(3)引き算の実行
0.6 = 1.0011 00110011 00110011 00110011 00110011 00110011 00110011 0 ×2^-1
-)0.4 = 0.1100 11001100 11001100 11001100 11001100 11001100 11001101 0 ×2^-1
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
0.0110 01100110 01100110 01100110 01100110 01100110 01100110 0 ×2^-1
(4)引き算の結果
0.0110 01100110 01100110 01100110 01100110 01100110 01100110 0 ×2^-1
(5)正規化その1(左へ1桁シフト)
0.1100 11001100 11001100 11001100 11001100 11001100 11001100 ×2^-2
(6)正規化その2(左へ1桁シフト)
1.1001 10011001 10011001 10011001 10011001 10011001 1001100 ×2^-3
(7)終わり
1.1001 10011001 10011001 10011001 10011001 10011001 10011000 ×2^-3
おわかりでしょうか。左シフトで下位ビットに新たに0が付加されます。つまり、引き
算する2つの数値が近ければ近いほど、計算結果の上位ビットには0が多く並びます。
これを正規化すると左シフトによって下位ビットに0が埋められてゆきます。これが桁
落ちする理由です。
(注)実際のコンピュータの計算では、(3)の引き算の実行は、引かれる数 0.2
の符号を変えて足し算が行われます。
この様に、「0.6 - 0.4」と「0.2」とは共に丸め誤差があり、それらは正確な値から
ずれています。非常に近い値の数の差によって桁落ちが生じて
0.6 - 0.4 - 0.2 = -1.000000×2^-54 = -5.55112e-17
という結果になります。
3.13.4 計算機ε
浮動小数点型データの値は、常に誤差幅(エラーバー)を伴っています。これは、2
つの浮動小数点数型の変数a、bに対して次のようなコードを書くことが、危険である
ことを意味します。
if( a == b ){
// ナンチャラカンチャラ
}
実際、次のように誤った条件判断をしてしまいます。
#include <iostream.h>
#include <math.h>
int main()
{
double a = 0.6 - 0.4;
double b = 0.2;
if( a == b )
cout << "「0.6 - 0.4」と「0.2」は等しい。" << endl;
else
cout << "「0.6 - 0.4」と「0.2」は等しくない。" << endl;
return 0;
}
|
[実行結果] |
「0.6 - 0.4」と「0.2」は等しくない。 |
この様な問題を避けるには、誤差幅の範囲内で浮動小数点型データの値を比較評価し ます。
#include <iostream.h>
#include <math.h>
#define epsilon 1.E-16 // 誤差幅
int main()
{
double a = 0.6 - 0.4;
double b = 0.2;
if( fabs(a - b) < epsilon )
cout << "「0.6 - 0.4」と「0.2」は等しい。" << endl;
else
cout << "「0.6 - 0.4」と「0.2」は等しくない。" << endl;
return 0;
}
|
|
[実行結果] |
「0.6 - 0.4」と「0.2」は等しい。 |
この誤差幅の大きさを評価する量として、次式で定義されるε(イプシロン)という 数が使われます。1.0 + ε > 1.0 となる最小の値ε εの値は浮動小数点型の変数が等しいことを示す目安となる量です。このεのことを計 算機ε (machine epsilon) といいます。 計算機εはC言語の標準ヘッダファイル float.h の中で、FLT_EPSILON(float型 の計算機ε)、DBL_EPSILON(double型計算機ε)、LDBL_EPSILON(long double 型計算機ε)という名前のマクロで定義されています。例えば、Borland C++ Builder では、 #define FLT_EPSILON 1.19209290E-07F #define DBL_EPSILON 2.2204460492503131E-16 #define LDBL_EPSILON 1.084202172485504434e-019L となっています。[注] 標準C++では、できるだけマクロの利用を避けるスタイルを取ります。 C++では、<limits>の中にクラス・テンプレート numeric_limitsが定義 されています。例えば、double型のクラスnumeric_limits<double> のなかのメンバ関数 epsilon()は、double型の計算機εの値を返します。 プログラムからは、次のように呼び出します。ここで、実際にdouble型の計算機εの大まかな値を求めてみましょう。詳しくは、Bjarne Strustrup:「プログラミング言語C++ 第3版」 (アジソン・ウェスレイ/アスキー)の第22章を参照ください。
// double型の計算機ε #include <iostream> #include <limits> using namespace std; // 標準ライブラリの名前空間を使う int main() { numeric_limits<double> limits; cout << "epsilon = " << limits.epsilon(); return 0;}
// epsilon.cpp
// 計算機ε(double型)
#include <iostream.h>
int main()
{
double epsilon = 1.0;
double val = 1.0 + epsilon;
while( val > 1.0 ){
epsilon *= 0.5;
val = 1.0 + epsilon;
}
cout << " epsilon = " << epsilon << endl;
return 0;
}
|
|
[実行結果] (ソースファイル epsilon.cpp) |
|
epsilon = 1.11022e-16 |
本当のεは、この値の2倍程度になります。epsilon 程度の大きさの差異のある浮動小 数点数は区別がつかないことを意味します。
[演習問題 3.11] double型の計算機εを求めるために次のプログラムを、あるコンパ イラを使って実行した。 #include <iostream.h> int main() { double epsilon = 1.0; while( 1.0 + epsilon > 1.0 ) epsilon *= 0.5; cout << " epsilon = " << epsilon << endl; return 0; } すると、予想より非常に小さな値(epsilon = 5.42101e-20)が得られた。なぜか?
3.13.5 行列の微少要素の除去
行列演算で生じた計算誤差のために、本来0となるべき微小要素を除去するメンバ関 数を実装します。
// matrix19.h
// 計算誤差による微少要素を除去する
#define NEARLY_ZERO 1.E-16 // ゼロと見なせる
#define ZERO_TOLERANCE 1.E-8 // 相対誤差
class Matrix; // 前方宣言
class Vector{
・・・・・・・
friend const Matrix operator*(const Matrix &, const Matrix &);// 行列の積
friend const Vector operator*(const Matrix &, const Vector &);//行列*ベクトル
friend const Vector operator*(const Vector &, const Matrix &);//ベクトル*行列
・・・・・・・
public:
・・・・・・・
void cleanup(); // 微少要素の消去
・・・・・・・
};
class Matrix{
・・・・・・・
friend const Matrix operator*(const Matrix &, const Matrix &);// 行列の積
friend const Vector operator*(const Matrix &, const Vector &);//行列*ベクトル
friend const Vector operator*(const Vector &, const Matrix &);//ベクトル*行列
・・・・・・・
public:
・・・・・・・
Matrix &operator*=(const Matrix &);
void cleanup(); // 微少要素の消去
・・・・・・・
};
|
メンバ関数 Vector::cleanup()、Matrix::cleanup()は、行列やベクトルの要素で、絶 対値が最大要素の値 max と比較して相対的に小さい値(マクロ ZERO_TOLERANCE より小 さい値)の要素をゼロにします。
// 微少要素の消去
void Vector::cleanup()
{
int i;
double max = 0.0;
// 最大要素 max を見つける
for(i = 0; i < Dim; i++)
if(fabs(ptr[i]) > max ) max = fabs(ptr[i]);
if( max > NEARLY_ZERO )
for(i = 0; i < Dim; i++)
if( fabs(ptr[i]) / max < ZERO_TOLERANCE )
ptr[i] = 0.0;
}
// 微少要素の消去
void Matrix::cleanup()
{
int i,j;
double max = 0.0;
// 最大要素 max を見つける
for(i = 0; i < Row; i++)
for(j = 0; j < Col; j++)
if(fabs(ptr[i][j]) > max ) max = fabs(ptr[i][j]);
if( max > NEARLY_ZERO )
for(i = 0; i < Row; i++)
for(j = 0; j < Col; j++)
if( fabs(ptr[i][j]) / max < ZERO_TOLERANCE )
ptr[i][j] = 0.0;
}
|
そして、このcleanup()を行列同士の積(*、*=)およびベクトルと行列の積(*) のメンバ関数の中で呼び出します。例えば行列同士の積では、
// 多重定義された*演算子
// 2つの行列の積を求め、値渡しで返す
const Matrix operator*(const Matrix &left, const Matrix &right)
{
if(left.Col != right.Row){//サイズのチェック
cout << "エラー:行列の型が一致しません\n";
abort();
}
Matrix mat(left.Row, right.Col); //一時的なオブジェクトを作る
for (int i = 0; i < left.Row; i++)
for(int j = 0; j < right.Col; j++){
double sum = 0.0;
for(int k = 0; k < left.Col; k++)
sum += left.ptr[i].ptr[k] * right.ptr[k].ptr[j];
mat.ptr[i].ptr[j] = sum;
}
mat.cleanup(); // これを追加!
return mat;
}
|
の様に、最後に演算結果を返す前に微少要素を除去します。 これらをヘッダファイル( matrix19.h )、関数定義プログラム( matrix19.cpp ) にまとめます。ソースファイルはこちら
- ヘッダファイル :matrix19.h
- 関数定義プログラム:matrix19.cpp
3.13.6 ガウス・ジョルダン法を使った逆行列の計算
ここで1つ例題を考えましょう。ガウス・ジョルダン法を使って逆行列を求めます。
[演習問題 3.12] 次の行列の逆行列を掃き出し計算(基本変形)で求めなさい。 | 1 2 1 | | 2 1 0 | | 1 1 2 | 回答はこちら。
上の演習問題の手計算と同じアルゴリズムでプログラムします。
// lst03_32.cpp // ガウス・ジョルダン法を使った逆行列の計算 // matrix19.cppと一緒にコンパイルする #include <iostream.h> #include "matrix19.h" double matinv(Matrix &);// 逆行列を計算 int main() { // 行列 double mat[3][3] = {{ 1.0, 2.0, 1.0}, { 2.0, 1.0, 0.0}, { 1.0, 1.0, 2.0}}; Matrix a(3,3);// Matrixクラスのオブジェクトを生成する // 行列の読み込み for(int i = 0; i < a.getRow(); i++) for(int j = 0; j < a.getCol(); j++) a[i][j] = mat[i][j]; cout << "行列:" << endl << a << endl; Matrix b = a; double det = matinv(b); cout << "行列式: " << det << endl << endl; cout << "逆行列:" << endl << b << endl; cout << "行列と逆行列の積:" << endl << a * b << endl; return 0; } // 逆行列を計算して上書きして返す // 関数の戻り値は行列式を返す double matinv(Matrix &a) { int n = a.getRow(); double det = 1.0; for (int k = 0; k < n; k++) { double p = a[k][k];// ピボット係数 det *= p; int i; for (i = 0; i < n; i++) a[k][i] /= p; a[k][k] = 1.0 / p; for (int j = 0; j < n; j++) if (j != k) { double d = a[j][k]; for (i = 0; i < n; i++) if (i != k) a[j][i] -= a[k][i] * d; else a[j][i] = -d / p; } } return det; } |
|
[実行結果] (ソースファイル lst03_32.cpp) |
行列: 1.000000e+00 2.000000e+00 1.000000e+00 2.000000e+00 1.000000e+00 0.000000e+00 1.000000e+00 1.000000e+00 2.000000e+00 行列式: -5.000000e+00 逆行列: -4.000000e-01 6.000000e-01 2.000000e-01 8.000000e-01 -2.000000e-01 -4.000000e-01 -2.000000e-01 -2.000000e-01 6.000000e-01 行列と逆行列の積: 1.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 1.000000e+00 |
もとの行列と、求めた逆行列の積は正しく単位行列になっています。
| 目次 | 前のページ | 次のページ | ページの先頭 |
Copyright(c) 1999 Yamada, K