








(A^8-A^4-A^-4)

(A^-8-A^-4+1+A^8)

(A^8-A^4+1+A^-8)
結びが同じかどうかの判定には、主に比較的計算が容易なブラケット多項式を使用した。
しかし何度も計算を間違えたので、くり返し出て来る形を整理した。
 |
 |
||||||
| 0 |  |
= | -(A^2+A^-2) | ||||
| 1 |  |
= | -A^-3 | 1- |  |
= | -A^3 |
| 2 |  |
= | -(A^4+A^-4) | 2- |  |
= | -(A^4+A^-4) |
| 3 |  |
= | A(A^-8-A^-4-A^4) | 3- |  |
= | A^-1 (A^8-A^4-A^-4) |
| 4 |  |
= | -A^-2 (A^-8-A^-4+1+A^8) |
4- |  |
= | -A^2 (A^8-A^4+1+A^-8) |
 |
 |
 |
 |
||||||||
| 1 |  |
= | A | + | A^-1 | 1- |  |
= | A^-1 | + | A |
 |
 |
 |
 |
||||||||
| 2 |  |
= | 1-A^4 | + | A^-2 | 2- |  |
= | 1-A^-4 | + | A^2 |
| 3 |  |
= | A^-1 (1-A^4+A^8) |
+ | A^-3 | 3- |  |
= | A (1-A^-4+A^-8) |
+ | A^3 |
| 4 |  |
4- |  |
 |
 |
 |
 |
||||||||
| 2 |  |
= | 1-A^4 | + | A^-2 | 2- |  |
= | 1-A^-4 | + | A^2 |
| 2 1 0 |  |
= | A (1-A^4) |
+ | A^-1 (1-A^4-A^-4) |
2- 1- 0 |  |
= | A^-1 (1-A^-4) |
+ | A (1-A^4-A^-4) |
| 2 1- 0 |  |
= | A^-1 (1-A^4) |
+ | -A^5 | 2- 1 0 |  |
= | A (1-A^-4) |
+ | -A^-5 |
| 2 2 0 | 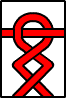 |
A^2 (1-A^4) |
A^-8-A^-4+2-A^4 | 2- 2- 0 |  |
A^-2 (1-A^-4) |
A^8-A^4+2-A^-4 | ||||
| 2 2- 0 |  |
2- 2 0 |  |