基礎3: 地表面の熱収支と気象
著者:近藤純正
研究課題
3.1 予備知識
3.2 熱エネルギーの流れ
3.3 熱エネルギーの大きさの実感
3.4 地表面の乾湿と温度
3.5 熱収支式
3.6 熱収支量と交換速度の関係
3.7 結露量と風速の関係
3.8 ボーエン比の気温依存性
3.9 熱収支量と地温の日変化
3.10 日射量の変動に伴なう風速変動
Q&A
文献
地球上の様々な現象は、地球に注がれる太陽エネルギーが源となっている。
太陽エネルギーの大部分は地表面に到達し、地球の表面を加熱し、
海面や土壌中の水分を蒸発させたり、直接大気を加熱している。
加熱の度合いに地域的な違いがあると気圧の分布が生じ、
風が吹き雨や雪が降る。
熱や水分の出入りのことを「熱収支、水収支」と呼ぶ。
熱エネルギーの流れの観点から大気現象を調べてみよう。
研究課題
冬期の積雪地域では、雪温が0℃まで上昇し融解するときは融解の潜熱を
費やすため積雪面温度の上昇は抑えられる。
逆に再凍結するときは凍結の潜熱を放出するため積雪面の夜間冷却は
弱められる。それゆえ、積雪地域において
融雪・再凍結が生じるような気象条件では気温の日変
化幅が小さくなることをアメダスデータから示す。
クリックして「ヒント」を参照し、
プラウザの「戻る」を押してもどってください。
3.1 予備知識
(1)蒸発量(正確には蒸発速度)の単位は mm/day, mm/s,
kg s-1m-2などで表わす。
(2)風速が大きいほど蒸発は盛んである。
(3)気温が高いほど蒸発は盛んである。
(4)空気が乾燥しているほど蒸発は盛んである。
(5)湿った地表面(海面、湖面)や植生地で蒸発は盛んである。
(6)日射量が多いところで蒸発は盛んである。
(7)蒸発面のスケールが小さいほど単位面積あたりの平均蒸発量は大きい。
上記(7)については、図3.1 で説明する。
図の左側は小面積の湿面(水面など)、右側は大面積の湿面とする。
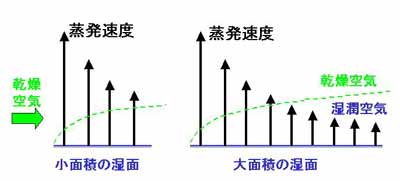
図3.1 蒸発面の大きさと平均蒸発量の説明図。
図の左方から乾燥した風が吹いてきたとすると、湿面の先端で蒸発量が
大きいが、風下に行くにしたがって空気は湿ってくるので、蒸発量は
先端からの距離とともに減少する。したがって、面積のスケールが小さい
ほど単位面積あたりの平均蒸発量は大きくなる。
植物葉面の気孔からの蒸発を蒸散という。
植生地の土壌面からの蒸発を含め、植生地からの蒸発を
蒸発散という。
降水中の濡れた葉面など樹体からの蒸発を遮断蒸発
という。
これらを区別せずに、総称して蒸発あるいは
蒸発散という
こともある。
図3.2 は日本の湖面からの年蒸発量の緯度分布である。低緯度では
年蒸発量が800~1,100mmであるのに対し、高緯度では500mm前後で
ある。
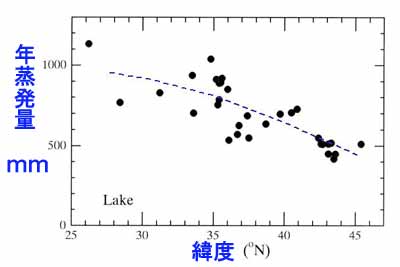
図3.2 湖面の年蒸発量の緯度分布。
(水環境の気象学、図14.5;表14.5に基づく)
低緯度で蒸発量が多くなる理由のうち、
もっとも効果的な要因は次のうちのどれか?(回答は3.8節、および
備考「湖面の年蒸発量と年平均気温」で学ぶ。)
(1)低緯度で日射量が多いこと。
(2)低緯度で気温が高いこと。
(3)低緯度で日照時間が多いこと。
3.2 熱エネルギーの流れ
地表面には各種のエネルギーが出入りしている。図3.3は主なエネルギー
の流れを示したものである。
地表面には太陽からの直達日射と散乱日射が入っている。
また、大気からの大気放射も入っている。
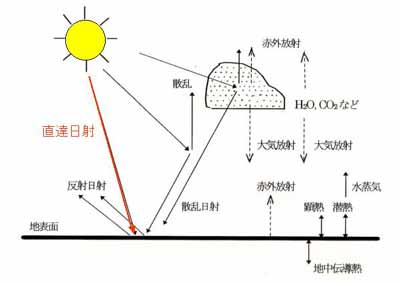
図3.3 熱エネルギーの流れ。(地表面に近い大気
の科学、図1.10、より転載)
日射量S↓:地球上における熱輸送量の大きさは太陽定数を基準に
するとわかりやすい。太陽定数とは,太陽と地球が平均距離のとき,
地球大気の上端において,太陽光線に垂直な単位面積に単位時間に
入射する太陽エネルギーI0のことで,
太陽定数:I0=1360±7 W m―2・・・・・・・・
・・・・・・・・・・・・・・・(式3.1)
である。大気上端に入射する太陽エネルギーの昼夜平均値は,
地球の半径を a とすると
大気上端の平均値=(地球に到達する日射量)/(全地表面積)
=πa2I0/4πa2=I0/4
=340 W m―2・・・・・・・・・・・・・・・・ (式3.2)
となる。
大気中には太陽光線を吸収したり散乱したりする空気分子,エアロゾル,
雲粒子などがあるので,地表面に入射する日射量S↓(地表面日射量,
略して日射量)は(式3.1)よりは少ない。
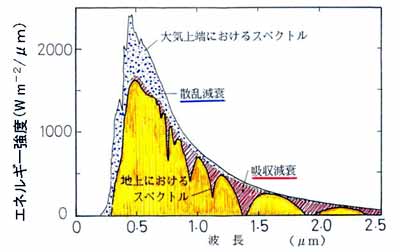
図3.4 太陽が天頂にあるときの太陽光のスペクトルの例。
(地表面に近い大気の科学、図2.5、より転載)
図3.4 は太陽光のスペクトルの例である。大気中の水蒸気量が多いほど
日射は大気中で吸収される分が多くなり、地表面に到達する量は少なくなる。
夏の中緯度における快晴日の正午の地上における日射量の目安は
1kWm―2である。
大気放射量L↓:大気中には温室効果気体があり,自ら赤外放射(熱放射,
または長波放射とも呼ぶ)を出すとともに,入ってきた赤外放射を吸収する。
水蒸気は大気組成の0.5%程度(時と場所で変動する)であるが,地表面に
入る大気放射量に最大の寄与をしている。次いで二酸化炭素(炭酸ガス)
とオゾンの寄与が大きい。黒体は,
その温度に応じた
最大の放射エネルギーを射出するのに対し,温室効果気体は固有の波長の
範囲で黒体以下の放射エネルギーしか出さない。
図3.5の実線は快晴時の
地表面へ下向きに入ってくる大気放射のスペクトルの例である。
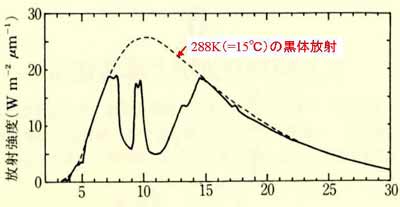
図3.5 大気放射のスペクトルの例。(地表面に近い
大気の科学、図2.12、より転載)
破線は288Kの黒体放射のスペクトルである。黒体に比べて,とくに
8~13μmの範囲のエネルギーが少ない。この波長範囲は
大気の窓
と呼ばれ,この範囲では,地表面からの上向きの赤外放射はほぼ素通
りして宇宙空間へ出ていく。
このことを利用して,宇宙から地球表面の
温度を,雲があるときは雲頂の温度を観測することができる。
このようにして測られた温度を「輝度温度」(相対黒対温度)という。
大気放射量は,大気中に水蒸気量が多いときには黒体放射(破線)
に近づくが,水蒸気量が少ないときには小さくなる。また,低層の雲が
厚いときには,大気放射量はその雲層の温度に対する黒体放射量に近くなる。
同じ水の量であっても,水蒸気(気体)は雲(液体または固体の水)に
比べて放射量を出さない。
大気放射量L↓の目安は,地上付近の日平均気温Ta(K)に対する黒体放射量
σTa4との比で表すとわかりやすい。
ただし,σ(=5.67×10―8Wm―2)は
ステファン・ボルツマン定数である。
図3.6は大気中の有効水蒸気量の関数として
大気放射量を表わしている。
有効水蒸気量とは可降水量(水蒸気をすべて
降り落としたときの降水量)
より20%程度小さい量である。
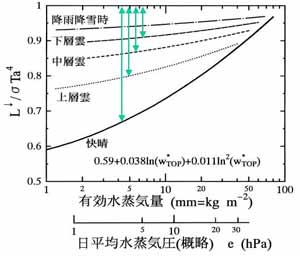
図3.6 大気放射量と有効水蒸気量との関係。図の下に地上の日平均
水蒸気圧の概略値の目盛も入れてある。緑色の縦線は、日平均気温が
日平均地表面温度に等しいときの、地表面における正味放射量の日平均値
にほぼ等しい。
(地表面に近い大気の科学、図2.23、より転載)
快晴時のL↓/σTa4は,水蒸気量が多いとき0.8~0.9,
水蒸気量が少ないとき0.6~0.7である。全天に雲があるときの
L↓/σTa4は,上層雲では0.8前後,
中層雲では0.8~0.9,低層雲や降水時では0.9~0.95である。
地表面の放つ赤外放射量:
上向きの赤外放射量はL↑=εσTS4
(TSは地表面温度)で表わすことができる。
磨いた金属(アルミや銅など)の赤外放射に対する「射出率」ε
は小さいが,地表面を構成する地物(土壌,岩石,草木,ビル,積雪)
や水面(海面,湖面)の射出率εは0.95~0.99であり,近似的に「黒体」と
みなしてよい。
地表面温度が20℃(T=293.2K)のとき、L↑=419 W m―2である。
顕熱輸送量 H と潜熱輸送量 lE:地表面温度が気温
より高いときは顕熱が地表面から大気へ,逆の場合は大気から地表面へ輸送
される。
その輸送のされかたは,基礎1で説明したように風の乱れに
よって行われる。通常,上向きに輸送される場合をプラスで表す。
潜熱輸送量は単位時間当たりの蒸発量(または蒸散量)Eと,
気化の潜熱 l の掛け算であり,
E=3.53mmd―1=1287mmy―1のとき,
lE=100Wm―2
に相当する。蒸発散量が多いところでは,日射によって地表面に
与えられたエネルギーの概略半分程度が蒸発散のために使われている。
湿度が高いときの夜間の陸面では凝結が起きる。また,水深が深い湖では
夏期の水温は気温に比べて低いことがあり凝結が起きる。
地中伝導熱(海や湖では水中伝導熱)G:日中,地表面に日射が入ると,
まず地表面付近の薄い地層の地温が上昇し,温度勾配ができて,
熱が地表面から深い層へ伝わる。夜間は逆に,地表面が冷却し,
下層から上に向かって熱が伝わる。この熱輸送量を
地中伝導熱 という。
通常,下向きをプラスで表す。
光合成エネルギー:植生地では日平均値で,太陽光エネルギーの
1%程度が光合成のエネルギーに費やされている。この大きさは,
通常,地表面の熱収支を考える場合は無視してさしつかえない。
3.3 熱エネルギーの大きさの実感
晴天日中の地上において、太陽光に垂直な面積に入る直達日射量は概略
1平方m当り 1kWである。したがって、窓ガラスの面積が延べ10平方m
あれば合計10kWのエネルギーが部屋に入ることになる。南側の部屋が
北側に比べて高温になるのはこのためである。
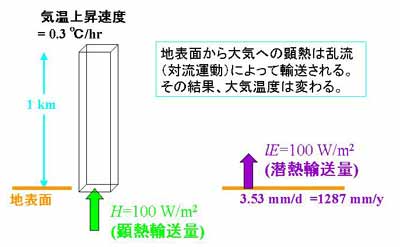
図3.7 顕熱輸送量の理解。
熱エネルギーの供給によって起きる大気温度の上昇量から、エネルギーの
大きさのイメージを掴んでおこう。図3.7は、地表面から1kmの厚さの大気
に100 W m-2が与えられたとき、大気の
温度は1時間に0.3℃の割合で上昇する。
潜熱輸送量100 W m-2は日蒸発量で3.53mmに、
年蒸発量で1,287mmに相当する。
気候学的には、年平均値 10 W m-2は年蒸発量128mmに
相当するので、乾燥地域の熱収支量を評価する際の精度は 10 W m-2
より高精度でなければならない。現実には、この精度で熱輸送量を通常の
方法で観測するのは非常に困難である。
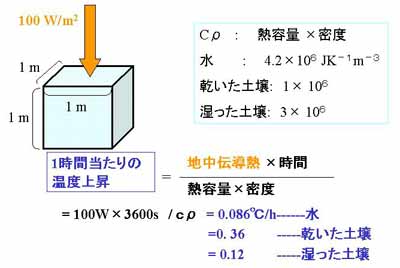
図3.8 地中伝導熱の理解。
地中伝導熱の100 W m-2は1m立方の土壌の温度を1時間に
0.36℃(乾いた土壌)、あるいは0.12℃(湿った土壌)の割合で
上昇させるエネルギーである。
しかし、実際の土壌は熱伝導率が悪く、1mの深さまで数時間で
は熱は伝わらない。そのため、1時間~数時間内には土壌表層(深さ0~0.1m)
付近の温度が著しく上昇する。
一方、海面表層では鉛直混合が盛んで、少なくとも厚さ1m程度の深さ
まではよく混合されていることが多い。図示の場合、1時間あたり
0.086℃の割合で水温の上昇が生じる。
海洋では、表層付近(深さ0~1m)の水温日変化の較差(最高温度と
最低温度の差)は1℃(弱風日)~0.1℃程度(風速10m/s以上の強風日)
である。
海洋や湖では,日射量のかなりの部分が水の
深くまで透過する。また,水中の鉛直混合によって熱を深くまで拡散し,
水面付近の水温の日変化は小さくなる。
その結果,顕熱・潜熱輸送量の日変化幅は小さい。
3.4 地表面の乾湿と温度
地表面温度は大気条件と地表・地中の条件に依存する。
最初に地表面で蒸発があるかないかによって、どのような日変化をするかを
見ておこう。
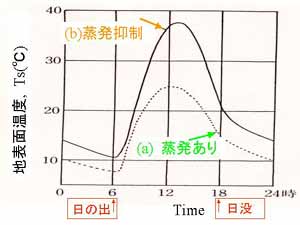
図3.9 蒸発がある場合(点線)とない場合(実線)の地表面温度の日変化
の例。(水環境の気象学、図6.6、より転載)
図3.9は春分秋分の晴天日を想定したときの、地表面温度の日変化である。
蒸発がある場合(点線)には、地表面では熱エネルギーの相当部分が水分を
蒸発させるために費やされ(潜熱輸送量が大きく)、地表面温度の上昇は
少ない。
蒸発を抑制した場合(実線)は、潜熱になる分がないので地表面温度は
上昇する。
日中の最高地表面温度は蒸発がある場合に比べて12℃ほど高温である。
夜間も4℃ほど高温である。
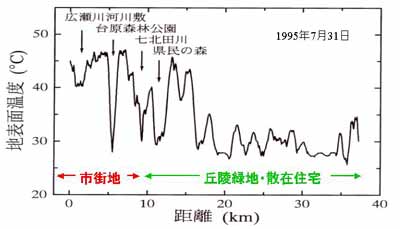
図3.10 ヘリコプターによる地表面温度の観測。
(菅原広史、私信;地表面に近い大気の科学、
図7.1、より転載)
図3.10はヘリコプターによって上空830mの高度から観測された
仙台市街から周辺の田園地帯にかけての地表面温度(市街部ではビルや住宅
の屋上、森林では樹冠部、水田ではイネの葉面の温度)の分布である。
台原森林公園や県民の森、七北川では30℃前後、丘陵緑地などでは28°程度
であるのに対し、市街地では45℃以上の部分が多い。蒸発の影響が地表面
温度を下げる働きをしていると理解できる。
水面のない広瀬川河川敷の温度は40℃程度であり、
ビルや道路に比べて低温である理由は何か?
①河川敷は白っぽく(アルベドが大きく)、太陽光の反射が大きいこと。
②河川沿いは風が通り抜ける「風の道」となる。
風が強ければ日中の地表面温度の上昇は抑制される。
一般に、地表面温度の日平均値と日較差は,
主に,地表面のアルベドと蒸発のしやすさ(蒸発効率、地表面の湿潤度)
によって変わる。蒸発効率が大きい(蒸発が大きい)ときは,地温の
日平均値は低く,地温変化の振幅も小さくなる。
3.5 熱収支式
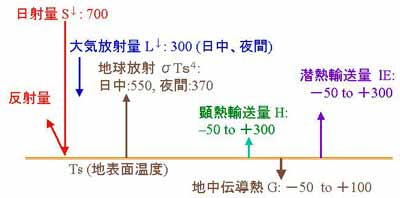
図3.11 地表面における熱収支。参考のために各熱収支量の代表値を
記入してある。
地表面では,各種のエネルギーが出入りしている(図3.11)。
その際,放射量をまとめた正味放射量Rn
が使われることが多い。
その理由の1つは,Rn は「正味放射計;放射収支計」という器械で
測られるという便利さからである。しかし,Rn は波長の違う短波放射(日射)
と長波放射(大気放射と地面からの赤外放射)をまとめた量であるために,
正確な測定値は得難いという欠点がある。
正味放射量 Rn の定義は,地表面のアルベードをref ,地表面温度
TSに対する黒体放射量をσTS4,
日射の反射の分を S↑とすると,
次式で表される。
Rn=S↓-S↑+L↓-L↑=(1-ref)S↓-
ε×(σTS4-L↓) ・・・(式3.3)
通常の地表面では赤外放射に対する射出率 ε は 1 に近いので,
以下では簡単化のために ε=1 とする。
地表面に入るエネルギーの正味放射量 Rn,出るエネルギーの
顕熱輸送量 H と潜熱輸送量 lE,さらに地中に向かう
地中伝導熱 G の収支関係は次の熱収支式で
表される。
Rn = H + lE + G ・・・・・・・・・・・
・・・・・・・・・・・・・・・・(式3.4)
この式はいかなる場合にも成立する基本式である。
ところで正味放射量 Rn は,すぐ近くであっても場所場所によって
地表面温度が10℃違うとL↑が50Wm―2程度も変わるので,
Rn におよそ50Wm―2程度の差ができる。
それゆえ,場所場所で Rn を観測しない場合や地表面温度を予知するときは,
次の熱収支式を使う。
R↓ = σTS4 + H + lE + G ・・・
・・・・・・・・・・・・・・・ (式3.5)
入力放射 = 地面放射 + 顕熱 + 潜熱 + 地中伝導熱
ただし入力放射量:
R↓=(1-ref)S↓+L↓ ・・・・・・・(式3.6)
S↓とL↓は水平距離で数m~数kmの範囲なら場所場所によってあまり違わないので,
熱収支式としては(式3.5) が実際的である。(式3.5) の左辺は一般に既知,
右辺は未知量である。熱収支式を解く目的は左辺が与えられているとき,
右辺の未知量(地表面温度,顕熱輸送量,潜熱輸送量,地中伝導熱)
を求めることである。
その際,気象条件(放射量,気温など),地表面のパラメータ(粗度など)
及び地中の熱的パラメータなどは既知とする。したがって,
対象とする地表面・地域については事前調査をしておく必要がある。
さて,数学の原理によると,未知量の数だけ式の数が必要である。
この場合は(式3.5)の他に,もう3つの式が必要である。
最初,G が無視できる簡単な場合を考える。陸地面において G は
日中・夜間でプラス・マイナスとなり,日平均状態を対象とするような
ときは無視できる。また,小物体や植物の葉面温度をTSとして
その凍霜害や結露量を考える場合にも G が無視できる。そのような場合には,
(式3.5) のほか2つの式を立てればよい。
それらは,バルク式と呼ばれる次の式である。
顕熱輸送量:H=cPρCHU(TS―T)
・・・・・・・・・・・・・(式3.7)
潜熱輸送量:lE=lρβCHU(qS-q)
・・・・・・・・・・・・・・(式3.8)
ここに,cPρは単位体積の空気の熱容量(cPと
ρは空気の
定圧比熱と密度),βは地表面の蒸発のしやすさを表す
蒸発効率(湿潤度と呼ぶこともある)であり0~1の値をもつ。
水面や積雪面でβ=1である。まったく蒸発がない乾いた面では
β=0であるが,大気の湿度が高くなり凝結が起きるようになると,
β=1である。k≡CHU は顕熱輸送の
交換速度,あるいは顕熱輸送の
コンダクタンス(その逆数を抵抗)と呼び,風速 U と大気の
安定度の関数である。また,地表面の種類(粗度の違い)によっても異なる。
TSは
地表面温度(一般には物体の温度,植生地では葉温),
qSはTSに対する飽和比湿(TS
の関数として数表または式で与えられる),
T と q は気温と大気の比湿である。
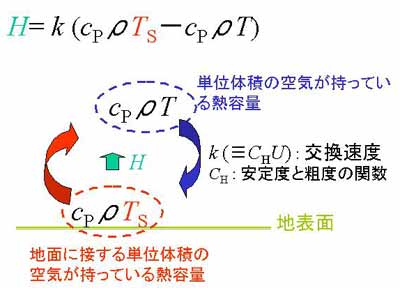
図3.12 バルク式と交換速度の意味の図式説明。
バルク式と交換速度の意味:
顕熱輸送の(式3.7)の右辺を書き直すと,
CHU(cPρTS- cPρT)
となる。cPρTSは地表面
すれすれの場所の単位体積の空気がもつ熱量であり,
cPρTは地表面から少し離れた高度 z の場所の単位体積の
空気がもつ熱量である。基礎1 で説明したように,
顕熱輸送は上下の空気塊の交換によって行われることを思いおこすと,
CHU はこれら2つの空気塊が交換される速度である
ことがわかる。
このことからCHUは交換速度と
呼ばれる。正しくは,
上下に交換される速度は鉛直速度 w の平均的な値であるが,
普通には w は測らないので,w の平均的な値と比例関係にある
平均風速 U で表している。その比例係数がCHであり,
バルク係数と呼ぶ。U は高度 z の風速であるので,
CHU は高度 z の関数であることは言うまでもないが,
地表面の種類ごとに,また,大気の安定度によって変わってくる。
3.6 熱収支量と交換速度の関係
3つの式(式3.5)(式3.7)(式3.8)を解けば、地表面温度と顕熱輸送量と
潜熱輸送量の3つを知ることができる。
晴天日中の草地の条件を想定する。この場合の顕熱輸送量H,
および潜熱輸送量lEと交換速度CHUとの関係を図3.13に示した。
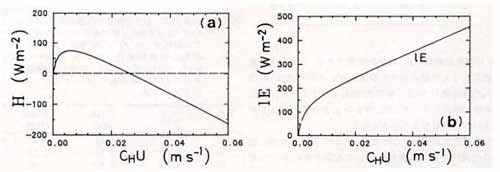
図3.13 交換速度と潜熱・顕熱輸送量の関係。
左図(a)によると,H は,初め CHU 、つまり風速とともに増加
するが,CHU=0.006m/s(CH=0.003の草地の
場合,風速2m/s)付近で極大値になったのち,
CHU=0.026m/s(風速で9m/s)付近で 0 となり,
以後マイナスの値で増加する。
これは,風速が弱いとき地表面は気温より高温になるが,
風速が9m/s以上では地表面は蒸発による冷却作用が強くなり
気温より低温になるからである。
右図(b)によると,潜熱輸送量は微風の
ところで急上昇するがCHU が概略0.012m/s(風速で4m/s)
以上になると直線的に増加する。やや湿った裸地でもこれとほぼ同様である。
この例では,風速が9m/s以下の範囲で H>0,それ以外で
H<0 ということは次の意味をもつ。下層大気は H>0 で温められるが,
H<0 では冷却される。これを広域の気圧配置による気圧の傾きが
ほとんどないときに生じる海陸風に当てはめてみよう。
海風は陸面上が海面上に比べて H が大きく,大気が昇温し,気圧が下降して
起こる現象である。海・陸で気圧差が生じて海風が吹き始めると,
陸上の H は大きくなり,大気はますます昇温,気圧差増加,風速増強の
過程を繰り返す。しかし,もし風速がある強さ(この例では9m/s)
以上になると,H は図(a) のように減少しはじめるので,風速は適当な大き
で平衡状態となる。平衡状態は,H の極大値をとる風速の近くにある。
この例では,風速2m/s程度で顕熱輸送量 H が極大値となった。
図示していないが,
β が小さいとき(地面が乾いているとき)ほど,H の極大値は風速の
大きいところで生じ,H の値も大きくなる。
したがって,他の条件が同じ場合,雨後の湿った陸面や
水田が多い地域では海風はあまり強くなれないが,乾いた陸面では海風は
強くなることが理解できる。
3.7 結露量と風速の関係
湿度が高い晴天夜間を想定し,地物の温度と各熱収支を計算すると,
凝結量が最大になるのは風速が適当なときに起きることがわかる。
こうした関係を
図3.14に示した。
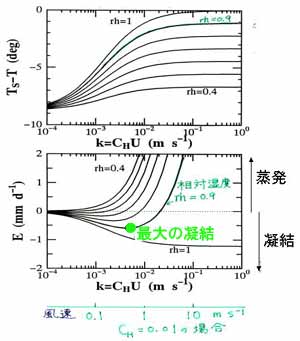
図3.14 下図は夜間の結露量と交換速度の関係、上図は物体(葉面など)温度
と気温の差を交換速度の関数で表わしたものである。
条件は気温=20℃、蒸発効率β=1、有効入力放射量R↓-σT4
=-50 W/m2、パラメータは相対湿度rh=0.4から1まで
0.1きざみであらわした。図の下の横軸にCHU=0.01 m/s の場合
(草丈0.1mの草地に相当)の
風速の概略値を示した。(地表面に近い大気の
科学、図5.7、より転載)
例えば,気温が20℃,相対湿度が90%の夜は,草丈0.1mの草地では
風速0.4~0.5m/s前後のとき最大の結露が生じる(緑色の丸印)。
これより微風では空気から地物へ輸送される水蒸気量(凝結量)は少なく,
また強風では地物の冷却が小さく結露は生じない。
早朝の草地をかきわけて歩くと、夜露で衣服が濡れる
ことがある。夜露の量は、風速と大気湿度に依存する。
3.8 ボーエン比の気温依存性
地表面に入射した放射エネルギーは顕熱輸送量 H と潜熱輸送量 lE に
分配される。その分配のされ方によって,大気への効果は違ってくる。
H が多ければ大気境界層は高温化されやすいが,
lE が多ければ多湿化が強い。
それらの比,H/lE はボーエン比と呼ばれる。
ボーエン比は熱収支量の観測から知ることができるが,熱収支式
からその振る舞いを調べることができる。
ここでは結果を見やすくするために,簡単な条件について計算しよう。
その条件とは,地表面が湿った水面や積雪面(すなわちβ=1),
大気の湿度は高く飽和,風速が非常に強いときとする。
計算の結果,顕熱輸送量 H,潜熱輸送量lE,ボーエン比 H/lE は,
次のようになる。
H=[γ/(γ+Δ)](R↓-σT4)・・・・・・・・ (式3.10)
lE=[Δ/(γ+Δ)](R↓-σT4)・・・・・・・・(式3.11)
H/lE=γ/Δ・・・・・・・・・・・・・・・・・・・・・・(式3.12)
ただし,γ=cP/l,Δ=dqSAT/dT,cP
は空気の定圧比熱,
l は気化の潜熱,qSATは飽和比湿である。なお,入力放射量 R↓
と気温に対する黒体放射量σT4の差、
R↓-σT4
を有効入力放射量と呼ぶ。
上記条件の場合のボーエン比,つまり γ/Δ は低温のとき大きいが,
高温のとき小さくなる。なぜならば、γ は近似的に定数と見なされる
のに対し、⊿ は図3.15の破線に示すように温度に強く依存するからである。
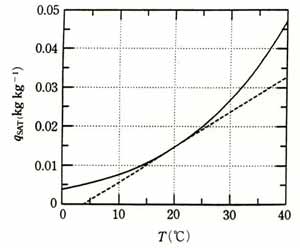
図3.15 飽和比湿と気温の関係(実線)。破線は温度 T=20℃における
勾配⊿である。(地表面に近い大気の科学、図5.3、
より転載)
結果の式が簡単になる条件について計算したが,一般に,
ボーエン比は高温のとき小さくなる。熱の配分則を高温時と低温時について
図3.16に比較して示した。
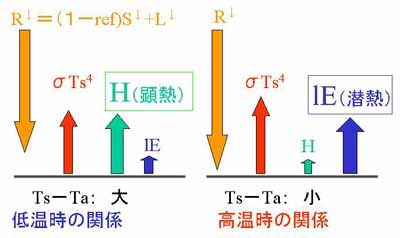
図3.16 エネルギー配分則、高温時と低温時の違い
ボーエン比について次のようにまとめることができる。
①ボーエン比(=顕熱輸送量/潜熱輸送量)は、
一般に気温が高くなるほど小さくなる。それは、高温空気ほど含みうる
水蒸気量が級数的に増加するからである。
②低温時に地表面(雪氷も含む)に熱が
加えられれば,大部分は顕熱として失われ,大気は直接加熱され,
蒸発はほとんど起こらない。
③逆に,高温の熱帯海洋や森林などでは,
地表面が吸収した放射量の大部分は蒸発のために使われ,
蒸発量が大きくなる。
④ボーエン比が小さいときは、大きいときに比べて、地表面温度と
気温の差は小さくなる。
ボーエン比の関係は人体についても同じである。ただし人体の場合は,
熱収支式中の入力放射量 R↓の中に人体発熱量(1日平均値は約100W,
表面積は概略1平方m)を含めて考える。人体は皮膚から放熱することで
体温調節を行っている。夏の熱いときは発汗・蒸発が主要な
放熱作用である。
海面や湖面ではボーエン比の気温依存性は
どうなるか?
「身近な気象」 → 「十和田湖物語」の説明を参照すると、
次の通りである。
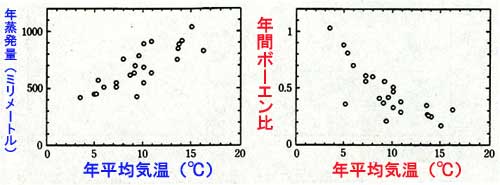
(付図3.1) 左図は日本各地の湖における年平均気温と年蒸発量の関係、
右図は年平均気温と年間ボーエン比の関係である
(「地表面に近い大気の科学」
(東京大学出版会、2000年)、図5.5 より転載)
年蒸発量は、年平均気温が高い南日本では700~1,000mm、
年平均気温が低い北海道では500mm前後である。
この詳細については、
次の「備考」をクリックして参照し、プラウザの「戻る」を押して
もどってください。
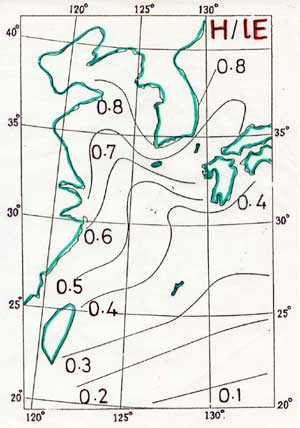
(付図3.2) 図は2月の東シナ海におけるボーエン比(=顕熱輸送量/蒸発の
潜熱)の分布である。(「身近な気象の科学」
(東京大学出版会)、図11.6 より転載)
ボーエン比は、北のほうで0.7~0.8、南下するにしたがって減少し
0.1~0.2となっている。つまり、北のほうでは顕熱輸送量が潜熱輸送量
より大きいが、南下するにしたがって逆転し、潜熱輸送量(蒸発量)
が大きくなることを表わしている。
冬期の東シナ海におけるボーエン比が北で大きく南で小さいという分布を
もつのは、「気団変質」の立場からみると、どういうことか?
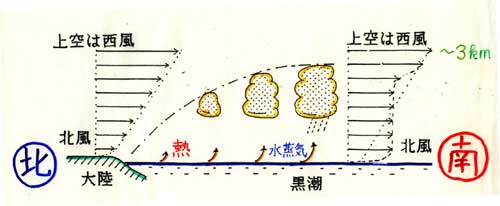
(付図3.3) 図は冬期の東シナ海における気団変質を模式的に説明したもの
である。(「身近な気象の科学」
(東京大学出版会)、図12.6 より転載)
大陸からの乾燥寒冷気団が暖かい海上へ吹き出してくると、
まず最初に、大気は相対的に顕熱の供給を受けて温められる。その空気
が南下すると海水は高温であり、こんどは相対的に顕熱よりは
潜熱、すなわち水蒸気の供給により気団は湿潤化し、対流混合が盛んに
なる。下層の水蒸気が上空へ運ばれ雲を発生して雨が降る。
つまり、気団変質は最初に温められたのち湿潤化するのである。
南方ほどボーエン比が小さいことを熱帯海洋に広げてみよう。
熱帯海洋上では、海から大気へ運ばれる熱の大部分は蒸発の形で
行なわれていることになる。大気が潜在的に不安定のとき、
つまり何かのきっかけで上昇気流が生じたとき不安定になる状態のとき、
積乱雲群が発生し、台風の発生・発達へとつながっていくのも水蒸気の供給に
よるのである。
3.9 熱収支量と地温の日変化
熱収支量と地表面温度の時間変化(日変化、年変化)を知るには
地中伝導熱 G を表わす式をも含め、4つの式を解き、4つの量(地表面温度、
顕熱輸送量、潜熱輸送量、地中伝導熱)の時間変化を求める。
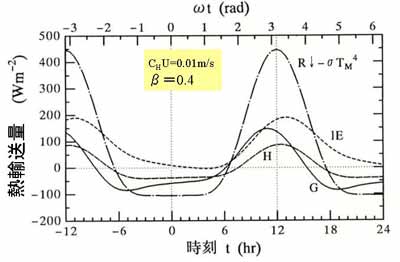
図3.17 熱収支量の日変化。(水環境の気象学、
図6.7、より転載)
図3.17は晴天日の地表面の各熱収支量の日変化である。この計算で与えた量
は一点鎖線で示す有効入力放射量 R↓-σTM4(R↓:入力放射量、
TMは日平均気温)である。
顕熱・潜熱輸送量(H, lE)は正午過ぎに極大値になっている。
しかし、地中伝導熱 G は正午前に起きている。
その理由は、G が最大になるのは、地表面温度の
上昇速度が最大のときに起きるからである。
次に、いろいろな地表面を想定しよう。
図3.18は晴天日の地表面温度の日変化を示し,破線は黒いアスファルト舗装面,
実線は草地,一点鎖線は新しいコンクリート面である。
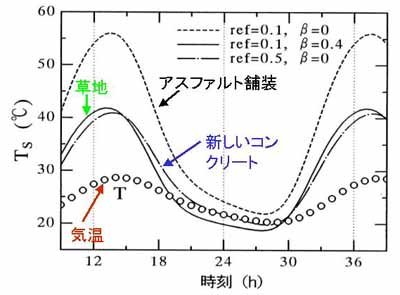
図3.18 各種地表面の温度の日変化、小さい白丸印は与えた気温日変化。
(地表面に近い大気の科学、図5.8、より転載)
アルベドの効果を見るために,アスファルト舗装面(破線, ref=0.1)と
新しいコンクリート面(一点鎖線, ref=0.5)を比較すると,
アスファルト舗装面では日中は約15℃も,夜間は約2℃も高温である。
蒸散の有無の効果を見るには、草地(実線、β=0.4)とアスファルト面
(破線、β=0)
を比べればよい。蒸散があると日中は約15℃も,夜間は約4℃も
低温となる。
従来,蒸散による温度低下の効果が注目されてきたが,
アルベドによる温度低下の効果はそれに匹敵している。
3.10 日射量の変動に伴なう風速変動
乾いた裸地面(地表層の熱的パラメータが小さく,
かつ蒸発効率βが小さい)では,地表面温度の変動幅が大きくなる
ことはすでに説明した(基礎2)。
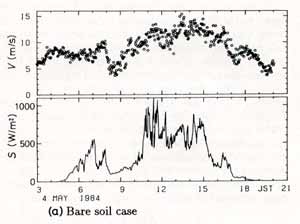
図3.19 乾燥した田んぼ上で観測した日射量の変動(下図)と高度5.2m
の地上風速の変動(上図)。
(Kondo and Kuwagata, 1992, より転載)
図3.19は田植え前の乾いた田圃で観測された日射量(下段)と
地上風速(上段)の時間的な変動である。
風は地形の大きな起伏や地表面の小さな凹凸(粗度)によって
乱流的に変動するが,この図では日射量の変動と風速変動の間に
相関関係が見られる。
こうした風速変動はなぜ起きるか?
日中、日射量が急に減少すると、地表面温度は急下降する。それに伴なって
大気の不安定度は弱まり、上下の鉛直混合が弱まる。逆に日射量が急上昇
すると鉛直混合が強まる。その結果、大気境界層内の風速鉛直分布は
「不安定時の分布」→「中立時の分布」→「不安定時の分布」を繰り返す。
すなわち、上空の風速が一定だとしても、接地層の風速は
強・弱を繰り返すことになる。
詳しい統計計算をしてみると,地上風速は数分間及び約0.7時間の遅れで
日射量の変動に追随している。数分間の遅れ変動は接地層(厚さ100m程度),
0.7時間の遅れ変動は大気境界層全層(2km程度)で地表面温度の
昇・降にともなって安定度の強化・弱化がおこり,地上風速の
増強・減衰が生じたものと考えられる。
積雪があるときについて解析してみると,日射量と地上風速の間には
相関関係は見られない。積雪はアルベドが高く,日射量をわずかしか
吸収できず,晴れたり曇ったりしても顕熱輸送量の変動は小さく,
乾いた裸地面上で見られたような現象は生じ難い。
Q&A
Q3.1:
「スケール数10kmの,ある広い地域で最高気温と最低気温が周囲に比べて
違うのは地下水の影響」と聞いたことがある。
ほんとうだろうか?
A3.1:地下水の影響によって,この地域が他に比べて地表面のごく近く
(深さ0~0.5m程度以内)の土壌水分が多く,また,植生により蒸発散が
盛んであるが,その他の条件は違わないとしよう。
この場合,(式3.5)によって熱収支的に考えれば,潜熱輸送量が大きいので,
地表面温度TSは平均的に低くなる。一方,土壌水分が多いことで,
地中の0~0.5m層の熱的パラメータが大きいとすると,地中へ出入りする
地中伝導熱が大きくなり,TSの日変化の振幅は小さくなる。
具体的には,
その地域と周辺での条件の違いを調査し設定すれば,潜熱の効果と
地中伝導熱の効果,その他の効果を見積もることができる。
実際には,土壌の種類や地表面のアルべドも変わることが考えられるので,
その点からも検討が必要である。
Q3.2:「都市はコンクリートが多いので、夜間の温度が下がりにくい」
と聞いた。図3.18によると、草地と新しいコンクリート面では1日の温度変化
が似ている。都市の温度が下がらない原因は何か?
A3.2: 図3.18はアルベドと蒸発効率の効果のみを示している。都市に限らず、
一般に地表面温度と地上気温は種々の原因が絡み合って決まっている。
温度上昇のプラス効果と冷却のマイナス効果があって、差引きプラスに
なれば、高温になる。
夜と昼では効果は異なり、また都市が存在することによって新しい風の
循環が発生することもあり、実際的には複雑である。また、小規模的には、
大きなビルができると、日陰になる部分は日中は低温になる。
夜間はビルからの赤外放射を受け、ビル街の谷間では、夜間の放射冷却
が小さい(菅原・近藤、1995、第5図)。
次に個々の要素について検討する。
①アルベド: 都市ビル群落が複雑構造になると、それ自体が全体として
アルベドを下げる効果がある。冷却に作用する。
②蒸発: 蒸発が少ないと昇温に作用する。
③人工熱: プラスの昇温に作用する。
④風速(熱交換速度): 通風がよい都市であれば熱交換が盛んで、
日中は涼しく夜間は暖かい。高層建築物が多いと、粗度が大きく乱流が
強く熱拡散が盛んでマイナスに作用するが、都市上の風速は弱まることで
プラスに作用する。
⑤熱的パラメータ: 都市構造物の熱的パラメータ(熱容量と
熱伝導率の積)が大きいときは日平均温度は変えないが、日変化の振幅
は小さくなる。水は熱的パラメータが大きく、単に、水辺を造れば涼しく
なるわけではない。深い(1m以上の)水辺が多ければ、温度は日中上がり
にくいが、夜間は下がりにくい。
Q3.3:森林では雨の日は濡れた樹木からの蒸発が多いので、大気は
冷却されているか? また、雨が降るとき気温が急に下がることがある
理由は?
A3.3: 森林では日射量がほぼゼロのときでも相当の蒸発量(日本では
年間、降水日約100日間に200~500mm)がある。このエネルギー源の
主要部は大気から森林への顕熱輸送である。したがって、大気は冷却されて
いることになる。
雨が降り出して気温が下がるのは、
①雨滴の周辺で冷却された空気が、雨滴群に引きずられて下降してくる。
②一般に、それまで高温に保たれていたとき、降雨に伴ない日射量が減少
すれば地温が下がり、地上の気温も下がる。
③連続的な降雨中には、濡れた樹木や地表面からの蒸発による冷却作用
がある。
文献
近藤純正(編著),1994:水環境の気象学-地表面の水
収支・熱収支-.朝倉書店,pp.348.
近藤純正、2000:地表面に近い大気の科学ー理解と応用ー.
東京大学出版会、pp.324.
Kondo,J. and T.Kuwagata, 1992: Enhancement of forest fires over
northeastern Japan due to atypical strong dry wind. J.Appl.Meteor.,
31, 386-396.
菅原広史・近藤純正、1995:都市における各種地表面温度の敏感度解析.
天気、42、813-818.
Yamazaki, T., 1995: The influence of forests on
atmospheric heating during the snow-melt
season. J. Appl. Meteor., 34, 511-519.





















