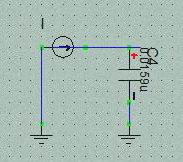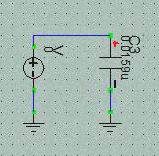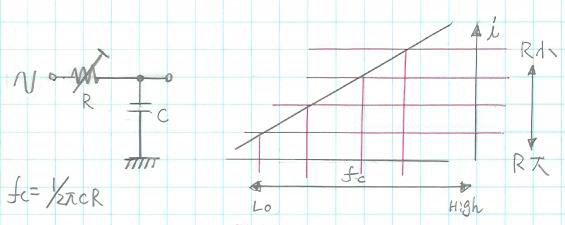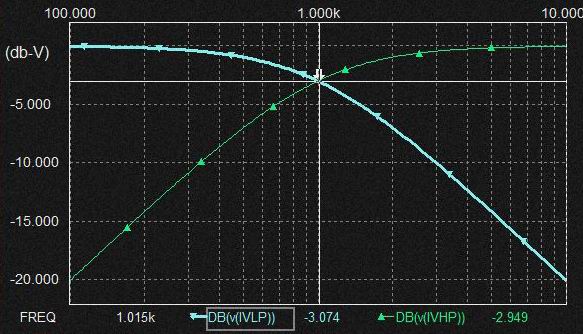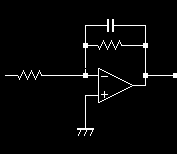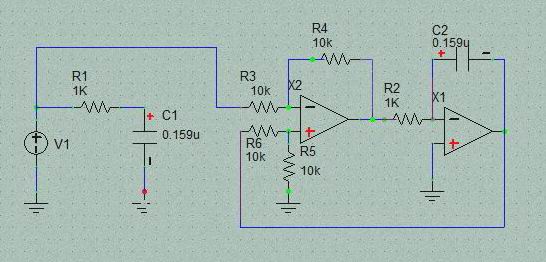
上図は両方とも1次のLPFです。 単純に考えると動作原理はCR LPFの方が簡単にも思えますが実際はCR LPFの方が動作が複雑に思えます。 すなわち右の OP AMPを2っ使った回路の機能をわずか1個のCとRでまかなっているので動作が複雑と言うか複数の動作が重畳されていると言うか。 LPFでありますが両者ともHPF動作もします。OPAMPの方はLPF/HPFのOutputともGNDレベルを基準に出力しますが、CR LPFの HPF出力はGNDレベル基準でなく抵抗の電圧降下です。
単純な1次のCR LPFは機能分離された回路でないのでけっこう感覚的な理解が難しいように思えます。 それに対して右側の回路は1次のSVFとも呼べるものですが機能が分離されていて動作意図がわかり易いです。 1次のLPFを考える前に Key Deviceであるcapacitorの性質を整理しておきましょう。
|
capacitorの基本性質
capacitorに電圧を直接印加する場合、直接電流を印加する場合の違い。
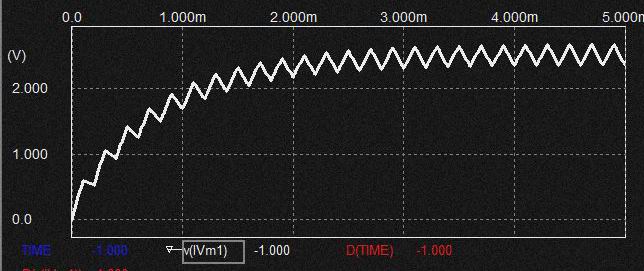
capacitorは電荷を蓄える為の装置です。 capacitorに定電流の直流を与え続けるとcapacitorの両端子電圧が充電によってリニアに上昇します(*1)。 このため理想的には与える時間が長いほど充電電圧が∞に上昇するということです。 また同じ電流値の交流を与えると充/放電電圧と印加信号周波数の関係は 1/f特性になります。 つまりcapacitorの充電電圧とは注入された電荷を積分した値となります。 この為capacitorは積分器とも呼ばれます。
*1: この場合、capacitorの容量が大きい方が電圧の上昇は遅い。
* 同じ振幅のSIN電流を与えても充電波形の振幅は変化する。 capacitorの充電電圧は流れる電流の積分なので上記のように周期の早い電流の方が電荷の蓄積量は少なく、充電電圧は小さな値になります。
V(t)= (1/C) * ∫i(t)dt
・定電圧の直接の印加
ではcapacitorに電圧を直接印加した場合はどうでしょう。
i(t) = C * dV(t) / dt 微分、積分が同時におこるメカニズムとしては印加された電圧と現在の充電電圧の差をうめるに必要な電流が発生し、結果瞬時にその電圧差を0にする作用、つまり印加電圧と充電電圧が同じになることで平衡(電流が止まる)しようとします。 つまり微分電流が発生してそれでcapacitorが充電されるということは必要以上に電流の流れが継続しないようにという自然の摂理というわけです。 capacitorに電圧を直接印加した場合一瞬で印加電圧との電位差が0になるということは、電流値に制限がかかっていない事です。(正しくは初めは制限がなく平衡した段階で電流制限最大) ですからcapacitorの容量が大きい方が充電するのにより多くの電荷が必要なので電流が多く流れますし、電流は電圧差の微分ですから電圧変化の差が大きいほうがまた電圧変化の激しいほうが大きい電流値となります。
橙: 微分特性 印加信号電圧に対応して微分特性電流が発生それが積分特性のCap.に入力されフラットな電圧特性(印加信号電圧とcap.の充電電圧が同じになる反応)となる。 capacitor単独回路においては、電流が流れることによりcapacitorに印加される電圧と充電電圧が同じになるわけですが、上記のように積分器の生の反応としては充電電圧は周波数に依存しますが、電圧がダイレクトでかかることにより、つねに印加電圧と同じ電圧が充電できるように周波数が高くなるに従ってより多くの電流が発生するように反応してつじつまが合うわけです。 capacitor 1個の反応でもよく見るとけっこう複雑です。 また上記の特性図は以下に示す1次filterの特性を予感?する要素を含んでいます。 すなわち微分特性としての電流特性は抵抗の電圧降下としてのHPF特性、積分特性はcapacitorの充電(放電)電圧としてのLPF特性の一部を現しておりcapacitor単体では印加電圧 = capacitorの両端子電圧 = 充電(放電)電圧なので顕著化しない性質が 抵抗1本を付加することで一部が現れ、あとは 2素子が電流を共有することによる負帰還による特性となる。
capacitorが未充電状態から印加電圧と充電電圧が一瞬で同じになって平衡する反応。 印加電圧が変動していればそれに追従する。 このことから印加電圧の変化にcapacitor端子が追従するために微分電流が発生しそれを積分した値がcap.の充/放電電圧となる。 このため容量が同じ capacitorに対しては印加電圧の変化が早ければそれに対応するために時間当たりの電流量が大きくなることでCap.の電圧が追従する。 変化がおそければ時間当たりの電流量が少なくても追従できる。 Zc = 1 / 2πF*C
Zc : capacitorのインピーダンス なので 印加される信号周波数が高い方がインピーダンスが小さくなる。 これは周波数が高いほど上記のように電流を大きくしないとCap.電圧が印加電圧に追従できないことからの反応。 また同じ周波数の信号に対してはCap.の容量が大きい方が印加電圧と充電電圧を同じにするのに必要な電流は多く必要なのでインピーダンスが小さくなり電流が増えるように反応。 ここらへんは意外と勘違いしやすい要素です。 capacitorに直接電圧を印加した時、電流は信号周波数増大に追従してリニアに増加します。 一方インピーダンスは非線形に1/Xで低下していきます。 よってX軸、Y軸を対数スケールに取ると電流は直線上昇、インピーダンスは直線低下で両者を掛けると電圧は一定値になります。
capacitor単体でなく抵抗を1本付加すると1次のLPF/HPFになります。 この場合抵抗により電流値が制限されてしまうのでcapacitorの両端電圧は瞬時に外部印加電圧と同じにはなりません。 両者の共有電流は印加電圧 - 抵抗の電圧降下で得られる電圧にcapacitorの両端子が充電するのに足りうる電流に制限され結果、 capacitorに印加される電圧と充電電圧はcapacitor単体と同様、瞬時に同電圧になります。 充電電圧は電圧源として機能するので外部印加電圧が固定であったなら充電電圧上昇で抵抗に加わる電圧は低下し共有電流も低下し、外部印加電圧と充電電圧が釣り合うと電流が0となります。 外部印加電圧が交流信号である場合は常に印加電圧が変化しているので電流=0にはなりませんが抵抗に印加されている電圧は外部印加電圧と充電(放電)電圧の差 となるわけで充電電圧は共有電流としての微分電流の積分値であることに変わりはありません。 |
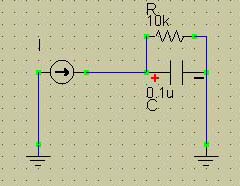
* 1次 CR LPF
単純には周波数に対するRとC の分圧比がLPFの特性となる。 印加信号電圧のRとCの分圧に対しては位相差が90度あるので(*1)印加信号と分圧された電圧との関係ははベクトルを使って対応するということで話が終わる説明が多いのですがそれでは事の本質がぬけているように思えます。
*1:上記のようにCapacitorにおいては電圧印加で微分、積分反応が生じ、直列回路なので電流は共通だがCapacitorの両端電圧は電流の積分結果だから。
Fc=1/2π C *R
FcはCとRのインピーダンスが同じになる周波数(cutoff周波数)。
Fcより低い信号周波数に対しては通過帯域で入力信号に近い振幅が得られ、高ければば遮断帯域となりその帯域の特性は 1/f特性となる。
1: 通過帯域では R < Zc
2: Fc R = Zc
3: 遮断帯域では R > Zc
Fcより1/10程度低い周波数の信号に対しては電流/電圧特性についてRはほぼ無視できる。
Fcより10倍程度高い周波数の信号に対しては電流特性についてはCがほぼ無視できる
Fcを中心として対数的に等距離にある低い方と高い方の周波数において(正規化)
入力SIN波の信号レベルを1V、 R=1K、 C=0.159uF とした時の各種値
| 周波数 | 抵抗比 | 直列抵抗値 | 電流 | C単独時の電流 | LPF電圧 | 入力との位相差 |
| 1000K | 1K:1 | 1000 | 1mA | 1000mA | 1mV | -89.9度 |
| 100K | 1K:10 | 1000 | 1mA | 100mA | 10mV | -89.5度 |
| 10K | 1K:100 | 1000.05 | 0.995mA | 10mA | 100mV | -84度 |
| 1KHz | 1K:1K | 1400 | 700uA | 1mA | 700mV | -45度 |
| 100Hz | 1K:10K | 10050 | 99uA | 100uA | 995mV | -5.8度 |
| 10Hz | 1K:100K | 100005 | 9.99uA | 10uA | 999.9mV | -0.6度 |
| 1Hz | 1K:1M | 1000000.05 | 0.999uA | 1uA | 999.99mV | -0.06度 |
Z = √(R^2 + Zc^2)
Fcより周波数が十分低いと Zc >> Rになるので 抵抗が無い時と同じだけ電流が Zc 支配 で流れる。 すなわち 抵抗があっても Cap. ONLYとほぼ変わらずのCap.を十分充電できるに足る電流が確保されるので印加信号電圧と近い値にCap,の両端子電圧がなる。
Fcより周波数が十分高いと R >> Zc となり電流はRで支配され制限される(*1)これは本来 cap.単体ではより飛躍的に電流が増える区間であるが電流が増えようとすればRによる負帰還すなわちRの電圧降下が高くなり電流は虚勢され一定値に近づくので十分 Cap.を充電できない状態。 この区間では電流がほぼ定電流化しており上記の定電流源の印加の状態に相当するのでCap.の 1/F特性が明確に現れるということになる。
LPF出力電圧は Zc * I という値で Cap.に加わる電圧が定義されので Zc の特性がそのまま出る。 これは直列回路の分圧という観点からみれば印加電圧が多くRにかかるようになるのでCap,に印加される電圧が低下することでCap.自体は分圧されて印加された電圧に対して即追従するための微分電流は確保されており印加される電圧が分圧されているのだからその分電流値は小さくてすむという反応です。
|
*1:
電流が完全にRに依存するのであればここでLPF出力は一定になってしまうのでこれは周波数=∞の時の話でそれまでは序所に抵抗オンリーの電流値に近づくの意味。 次の"1次 CR LPFのからくり"の項目で示すようにLOGスケールの周波数特性グラフにおいてはF=2KHz以降はほぼ 印加電圧 /Rの抵抗値で決まる電流値で推移しているように見えるので一瞬 Rの電圧降下には変化がなくなってしまうように見えるが、LPFの電圧特性を見れば出力は 1/f特性で低下しているので抵抗の電圧降下も大きくなっているがこれはX、Y軸をLOGスケールに取っているから見えるマジックでもある。 X軸、Y軸を LOGでとるか LINEARで取るかで受ける印象はかなり違ってしまう。 以下にそれぞれのスケールの違ったLPF電圧出力を示す。 最後の X、Y軸リニアスケールのグラフで見れば実際抵抗の電圧降下はほとんど増えていないのがわかえる。 電流特性は最後のグラフの逆特性であるからX、Yリニアスケールで見ればほとんど電流値はRによって決まる。 感覚的には X軸のみ LOGスケールのグラフがイメージをつかみやすい。 蛇足ついでに 1次CR filterはつまるとこCとRの直列接続の分圧の話であって一方の特性がリニアで他方が EXPOの特性を持っている。 上図において X軸のみLOGスケールのグラフを見るとどこかでみたことがあるようなグラフ、差動増幅回路の電流特性のグラフにそっくりでありさらに X、Y軸をLOGスケールで取ったグラフは 差動回路の Vbeの電圧特性にそっくりである。 これは差動回路においては両 Tr.の B-E間の直列接続に対する分圧を扱ったものなので基本、両者はEXPO特性を持った素子の直列接続という共通点がある。
|
Zc>>Rの区間においては差が大きいほどLPF出力位相は印加電圧位相との差= 0に近づき電流はcap,主体なので位相差が90度に近くなりそれを積分した LPF outとしての Cap.電圧位相が0と言う反応になる。 すなわち電流値が最少で電圧値が最大の時にLPFの位相差は0。
一方電流値最大時は R >> Zcなので電流発生はRが主体となるので差が大きいほど電流そのものには位相差がなくなり抵抗の電圧降下の印加電圧に対する位相差は0に近くなる。(LPFと逆特性のHPF出力) この時 LPF出力電圧自体は0に近づくが抵抗の電圧降下とCap,の電圧との間には信号に対して90度の差が常に生じる必然があるのでLPFの位相差は90度となる。
よって抵抗の電圧降下とCap.の電圧間は位相差90度が保持されていて両者の勢力差に応じて印加信号とのfilterの出力間に0から90度の位相差を生じる。 すなわち印加信号がSIN波ならば
A* sin(θ) + B*cos(θ) =√(A^2+ B^2) * sin(θ +α)
と言う三角波の合成公式そのものが1次 LPF(HPF)でおきる反応なのですが、タオのマークのように信号波形が抵抗波形とCap.波形に形は同じだが位相差を伴ってうまい具合に分割される現象はなかなか感覚的に理解できない部分ではないかとも思います。
また上記のようにSINとCOS波でなくとも同一周波数の正弦波は位相がずれて振幅が異なっても加算結果は正弦波になります。不思議ですね。また同一振幅の正弦波を位相差0度から180度変化させ足した正弦波の振幅はCOS波の1/4周期の値を反映したものになります。
上記の式は微分電流とそれを積分した結果のLPF電圧および微分電流が抵抗の電圧降下でHPF電圧になる反応を示しているわけで両者は位相差90度でありかつ印加される正弦波と同じ周波数になることを示しています。
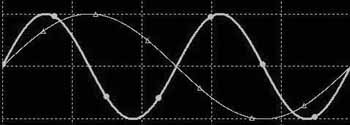
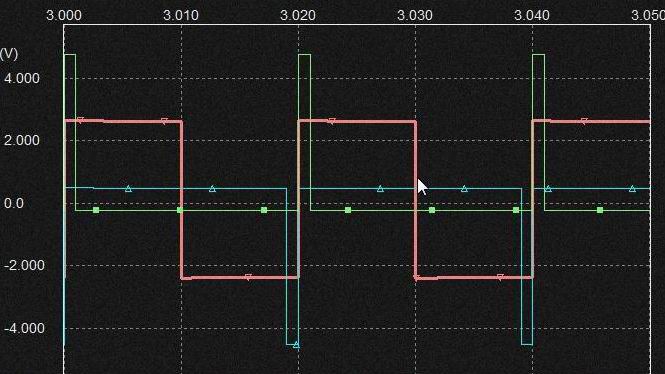
* CR filterの波形(位相差の発生)
* SIN波とCOS波が一つの正弦波の中に内包できるしくみ
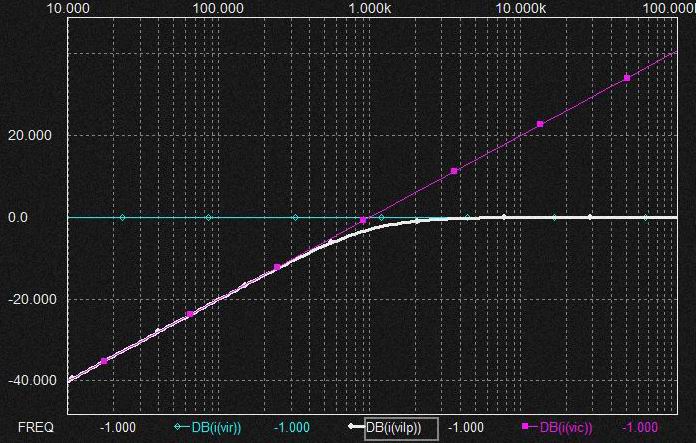
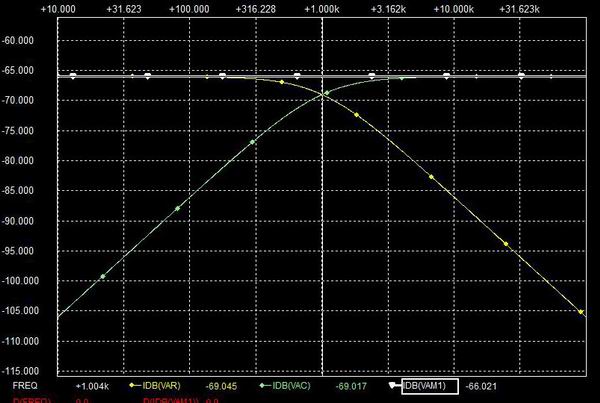
* 1次 CR LPFのからくり
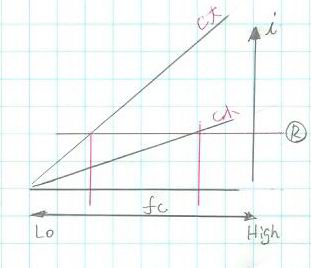
水: 抵抗単体時電流
桃: capacitor単体時電流
白: LPF電流
Fcより周波数が低い帯域ではCap.のインピーダンスが支配的でFcより高い帯域では抵抗の抵抗値が支配的になる。 結果、低い帯域ではCap.の素の特性が有効で高い帯域では電流値の上昇が抵抗の負帰還で押さえられ平坦化する。 よってCap.単体時の電流曲線と抵抗単体時の電流直線を漸近線として CR回路の電流特性が決まる。 Fcの周波数では両者が同じなので抵抗、 Cap.の交点がCR filterの電流値になりそうだが電圧波形と電流波形の位相差から交点の-3dB下がったポイントの電流値となる。 電流特性はHPF特性そのものなので抵抗の電圧降下は HPF。
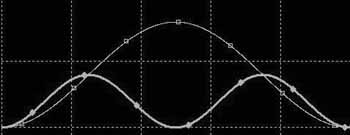
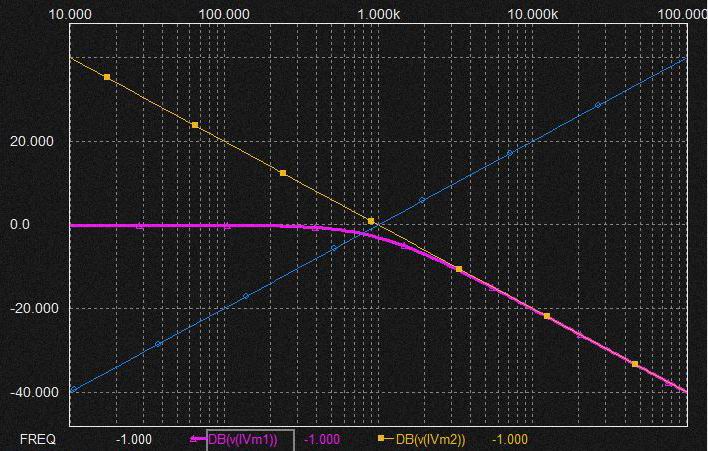
橙: capacitorの1/F特性
桃: LPF電圧特性
青: capacitor単体時電流(微分特性 F/1)
理想積分器の電圧特性としては Fcで GAIN=1、F=∞で0、 F=0Hzで∞となるがFcより高い帯域では上記のように積分器に印加される電流はほぼ一定値となるため積分器特性は素のまま表れ、Fcより周波数が低い帯域では電流特性は Cap.のインピーダンスを反映して1/f特性の逆の f/1特性となりその電流が積分器の1/f特性を通過するためほぼ一定の特性となる。 この場合も電流と電圧波形の位相差を反映して Fcでは -3dBのゲインとなる。 抵抗の漸近線にちかければ印加信号との位相差は0に近く、Cap.の漸近線に近ければ位相差は90度に近くなる。 当然 Fcでは45度の差。
Fcより十分周波数が低い領域では上記のcapacitorにダイレクトに定電圧を印加した時と同じような動作なので(*1)出力電圧特性はフラットに近い。 一方Fcより十分高い周波数帯域では定電流源にダイレクトにcapacitorを付け反応に近いので出力電圧特性は 1/f特性となる。 Fcの周波数前後では抵抗とcapacitorのインピーダンスが近い値になっているので両者のせめぎ合い。 電流が大きいほど抵抗の電圧降下が高くなるので出力電圧は減る。
*1:
Rに較べてCap.のインピーダンスが十分高いということは印加電圧がCap.にほぼかかるということでRが無視できるという意味。
|
上記のようにFc以前は定電圧をCapacitorに与えた関係、Fc以降はcapacitorに定電流を与えた特性に近くなるというしくみになるので初めに述べた定電圧と定電流の特性が内包された周波数特性となる。
一見、積分器の特性がFc以前の帯域では負帰還によって虚勢されているのではと思ってしまうがCRのpassive Filterの場合はFc以降の帯域でcapacitor電流に負帰還がかかって一定電流になる。 以下に示すOP AMPの加減算器 + 積分器の回路においては積分器の電圧特性に対して負帰還がかかるという違いがある。 LPFとHPFの関係は裏と表のような関係にあり両者を足すとフラットな特性になりこれは結局はCとRの直列回路なので当然ではあるが特性の異なる2素子間に共通に流れる共有電流は両者の基本特性を反映して生じるため単純なCとRの2素子であっても抵抗2本の分圧ほど簡単なものではなく動作は結構複雑な物となり上記のように印加信号が正弦波であればSIN波とCOS波に分割されみごとに存在する複雑な反応となる。 |
|
*1: 微分特性、 積分特性に近い領域では微分特性 * 積分特性でフラットな特性。 X,Y LOGスケール上では単純に足し算をした結果が一定直線 (0dB) |
|
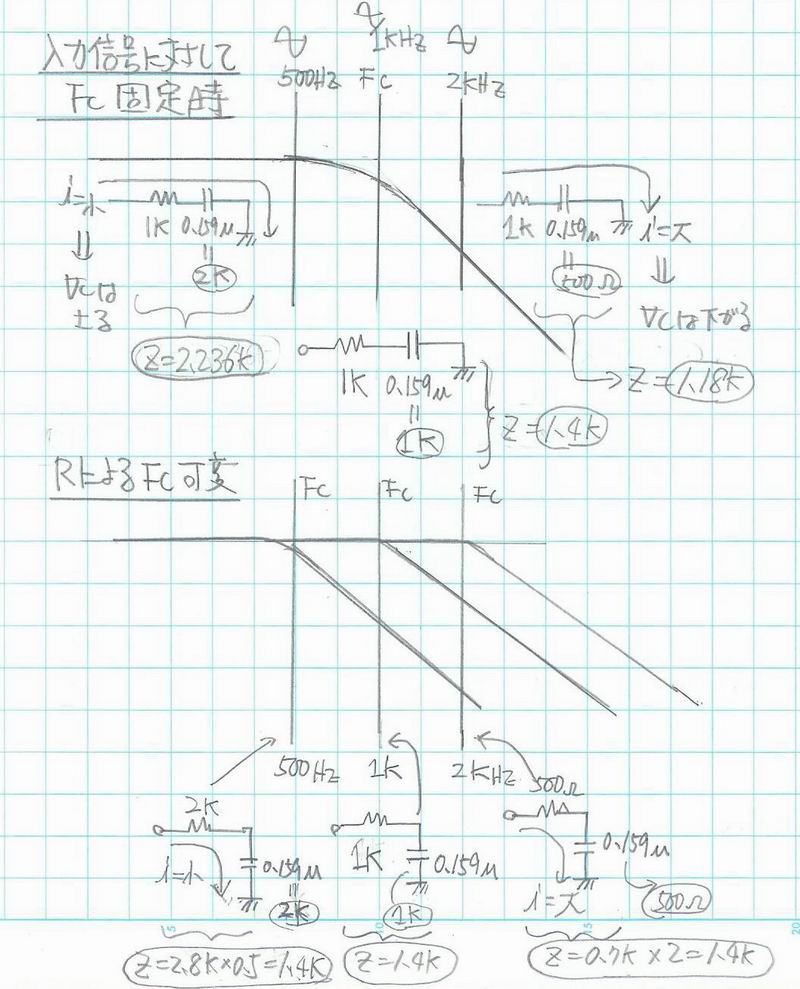
fc=1/2πCRの意味は
抵抗値が同じになる条件から、抵抗が小さい時の方が電流制限が少ないのでfcは高く、抵抗が大きい方が電流制限は大きいのでfcは低い。 *: Rが小さければCap.のインピーダンスと同じになる周波数Fcは当然高くなる。 *: Fc以降が遮断領域、Fc以前が通過帯域というFcはブレイクポイント。
Cの容量が大きい方がインピーダンスが低いのでC単体の電流特性は急(大きい)よって上図においてCが大きい方が fcは低い。(Rによる電流制限をより受ける)
信号周波数に対するcapacitorのインピーダンス変化は変わりませんがFcはRとCapacitorのインピーダンスが同じになる周波数であることに注意。
|
|
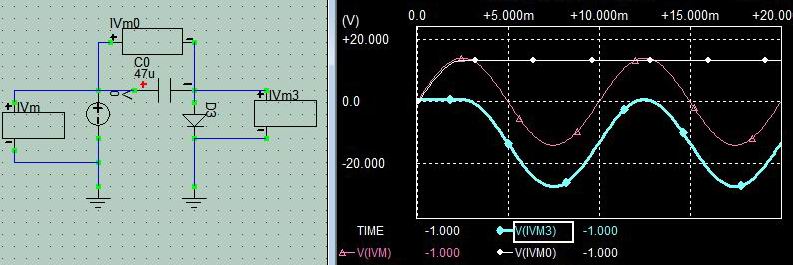
余談
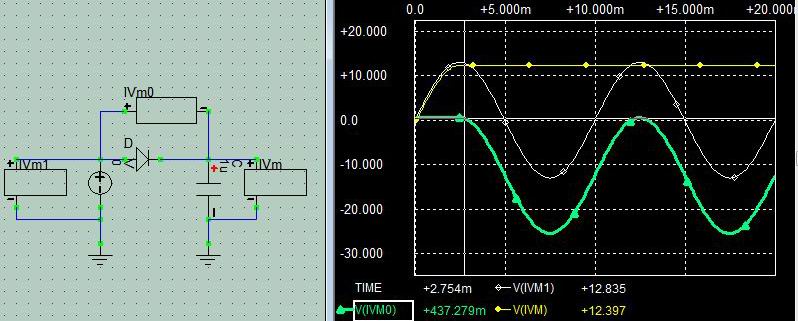
この場合DiodeはSWとして機能するのでCR filterににた直列接続であっても動作が全然異なります。 初期状態ではcapacitorは印加電圧と同じになろうとして充電されていきますが印加SIN波のピークを過ぎるとDiodeがOFFして以後電流がながれません。 すなわちcapacitorの充電電圧はSIN波のピーク値を保持することになり、一方Diodeの電圧はDiode OFFなので印加信号電圧がそのままでそうですが間にccapacitorによるDC電池が介在するので図Aにおいてはピーク電圧分レベルシフトしたSIN波が現れます。また図Bにおいてはピーク位置のDC電圧がCap.にたまっている状態。 電流が流れていないのだからCap.の印加電圧側の電位が動けばそれに連動してdiode側の電位も同じだけ動くのでCap.の電位は変化せず、間接的のDiodeの電位が印加信号にして動く。 これによって印加電圧 = capacitor電圧 + Diode電圧の関係を満たしていることになります。 感覚的には結構不思議に思える反応かと思いますがCapacitorの本質が出ている点だと思い書いてみました。 図Bでoutpiutに負荷がある場合はDiode OFFの期間で放電が起こるのでCapacitor電圧は低下し、SIN波のAC印加信号がOutput電圧より上昇すると再度DiodeがONの間充電が始まります。 充電区間はcapacitorのAC電圧に対する反応、放電区間はDC電圧に対する反応のように見えますが結局はつなげられた電圧とCapacitor電圧が同じになる反応であることには違いません。 |
同じ1次のLPFでもCR回路は微分電流に対して負帰還がかかりますが、以下のOP AMPの積分器を使ったものは積分特性に対して負帰還がかります。
ちなみに1次の filterは正帰還要素も無く、内部に BPF要素も内包していないので1次filterにおけるQの値は0.7で固定でいわゆるresonanceを可変することも発振することもできません。 そもそもpoleの位置がF=0のDCになるわけですから。
* 1次SVF?
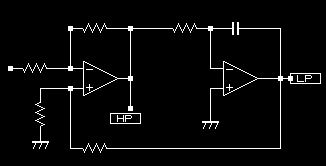
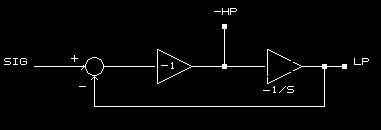
こちらの回路は機能分離されていてかつ電圧変化だけのやり取りなのでわかり易いです。 すなわちOP AMPによる積分器とOP AMPによる加減算器で構成された、積分器の出力を100%入力に負帰還する回路で 1次filterの本質を明示している回路です。 OP AMPのボルテージフォロワやエミッタフォロワ回路と同様の負帰還回路ですが一点、印加信号の周波数でGAINが変わる増幅器を内包しているという違いがあります。
はたして1次 SVFという名称があるのかわかりませんがこの回路にもう1段、積分器をつけると2次の SVFになるので便宜上こういう呼び方をしています。 2次のSVF同様この回路は2っのfilter 出力を持っています。 1次の CRfilterにおいてもLP、HP出力は可能ですがこの回路のように GNDレベルを基準にしての同時出力はできません。
図のOP AMPの積分器は出力のGAINだけを考えれば、印加される信号の周波数によって 増幅度が変化する増幅器と見ることができます。
Fc=1/(2πC*R)
GAIN= 1/2πf*C*R
なので 原理的には f=Fcで GAIN=1、 f=0でGAIN=∞ 、 f=∞でGAIN=0 となり GAINは 1/f特性となるわけです。 これは積分器なので当然のことなのですが、 印加される信号の周波数が0にちかくなるとGAINが非常に大きくなるわけでその信号を負帰還させて印加信号と加算すると LPF出力としての通過帯域が入力信号レベルに非常に近くなるというのがみそなわけなのです。(積分器の位相差が90度ある為、Fcでは入力信号1に対して振幅が0.7となってしまいますが....)
ちょっと考えるとf=0で GAIN=-∞ +印加信号(=1) が LPF出力と同じ(=1) に成るの??と思ってしまいますが、これには負帰還作用のマジックが作用しているわけです。
積分器は印加信号周波数によってGAINが変化するとともに積分器なのでSIN波を入力すれば位相が90度遅れるわけですが、ここで負帰還を理解する為に、上記回路の積分器部分を下図のような反転増幅器にかえてこの増幅器のGAINを可変したらどうなるかを考えてみます。
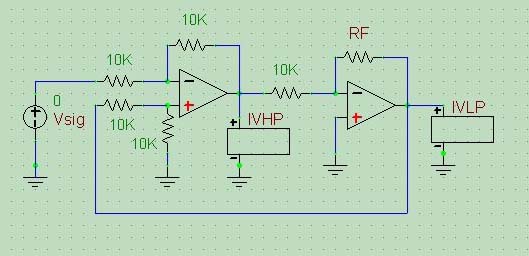
* 積分器が増幅器だった場合
| 増幅器のGAIN | HP出力 | LP出力 |
| 0 | -1 | 0 |
| 0.5 | - 0.666 | 0.333 |
| 1 | -0.5 | 0.5 |
| 2 | -0.333 | 0.666 |
| 4 | -0.2 | 0.8 |
| 5 | -0.166 | 0.833 |
| 6 | -0.143 | 0.857 |
| 7 | -0.125 | 0.875 |
| 8 | -0.111 | 0.888 |
| 9 | -0.1 | 0.9 |
| 10 | -0.0909 | 0.909 |
| 100 | -0.0099 | 0.990 |
| 1000 | -0.00099 | 0.999 |
印加信号(SIG)の振幅が1の場合、上記の結果を得ます。 すなわち増幅器の増幅率が高いほどLP出力はSIGに近づくということです。
* HPout=-{1/(GAIN+1)}
* LPout=HPout*-GAIN =GAIN/(GAIN+1)
つまり上式の関係が成り立ちますので GAINが大きくなればなるほどHP出力は小さくなり、LPの出力は限りなく印加信号レベルに近づく。
これは増幅器のGAIN自体は負帰還ループに影響されないということから導かれる反応あって、この条件が成り立つようにHP,LP出力は動作するということでもあります。
ここでも素子(この場合AMPの増幅度)の基本性質は単体でも回路内でも変化しないという作用の結果であるわけです。
|
これは増幅器を負帰還して使う場合と同じわけで、たとえば OP AMPのボルテージフォロワーを考えれば OP AMPの GAINは大変大きいという前提がなりたつから出力 = 入力振幅、つまり印加信号 = 1の振幅なら、出力振幅が1となりここで上記の HP出力に相等するのが OP AMPの +と-端子の電圧差になるわけで、 GAINが大きければこの差は0に近くなるのでイマジナリーショートになるわけです。
ここで 裸特性としてGAIN =1の OP AMPがあったとすればそのボルテージフォロワーの出力は印加信号振幅を1とすれば上記の表の通り 0.5になり、+端子と-端子の差も0.5となるわけです。 |
ここで GAINの部分を積分器に戻すと、
積分器=1/S
* HPout=-{1/((1/S)+1)}= -{S/(S+1)}
* LPout=(1/S)/((1/S)+1)= 1/(S+1)
となり 1次filterの一般式になるわけです。
積分器に戻って積分器のGAIN特性は 1/fになるのでSIN波の印加信号周波数が高い方から低い方に推移した時の振幅特性は周波数、振幅軸をLOGスケールにするとリニアな特性に見えるわけです。(左肩上がりの直線)
あとは積分器なので印加されるSIN波の位相が90度遅れるので、OP AMPの積分器部分では +90度の位相進みとなりそれが初段のOP AMPのマイナス端子に帰還されるので純粋に位相差180度の負帰還というわけにはならず、180度になるのは限りなく印加信号がDCに近い時のみとなります。
またGAINに対するLP,HPの出力レベルも上記の単純増幅器の場合と同じ出力振幅結果にはならず、位相差の影響で加算結果が複雑になるわけです。
この為、積分器の入出力位相差は90度固定であっても LPF出力と印加信号との位相差の関係は 0から90度まで入力信号周波数によって変化するわけです。 DCから周波数無限大の区間の中心ポイントがFc位置で位相が45度となるスケール感が不思議という感じがしますがFc位置ではGAINが1,DCでは無限大、周波数無限大では0という正規化周波数の中心がFcという関係です。
積分器のGAINが-1の時を考えてみましょう。 この時、HP出力振幅=LP出力振幅であり両者の位相差90度なので HP,LP出力と印加信号出力の関係は 1:1.414となるので印加信号を1とすればHP,LP出力は約0.7となるわけです。
上記の表でわかるように負帰還ループ内に増幅器があると増幅器の本来の増幅度は保障されなければならなく増幅器の裸GAINが大きくなればほどLP出力は1に近づくので必然的にHP出力は小さくなる反応が生じます。
積分器がループ内に入っているfilter回路では入力信号周波数によって積分器のGAINが変化するわけなので LPF出力が1に近づくつまり信号周波数が低くなるほどHPF出力は小さくなり DCで0になるわけで、Fcでは積分器のGAINが1なのでLPF=HPFになるわけです。
また 印加される信号周波数がFcより高くなるに従って 積分器のGAINは1より小さくなっていくのでその出力を入力に負帰還しても影響力が減ってきてLP出力は積分器の裸特性に近くなるわけです。
LPFの出力 = HPFの出力*積分器の増幅度
HPF出力 = LPFの出力* 1/積分器の増幅度という関係です。
つまりHPF出力が信号周波数が低くなるほど小さくなるのは積分器のGAINがどんどん大きくなるからで、そのHPF出力が積分器を通ることによりその時の積分器の増幅度によって元の LPF出力と同じ値に復元されるというわけです。
ですから1ポイントの周波数でみている分には初めの単純増幅器の負帰還と同じ作用に位相が90度遅れる要素を追加したものが1次のfilterなのです。 位相差が発生するので振幅はピーク値の単純加算では無くなりますが、
結局帰還ループ内で状態が安定しているということはLPF出力-印加信号でHPができてそれが積分器でLPに復元されるように平衡するということであり当然のことながら積分器の前と後の特性が裏表の特性になるということです。
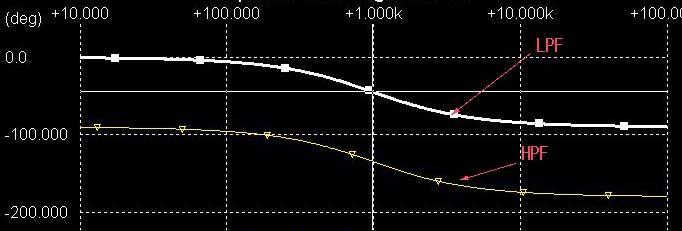
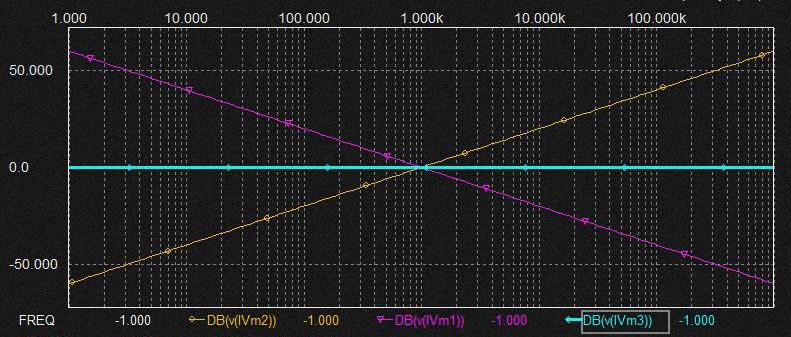
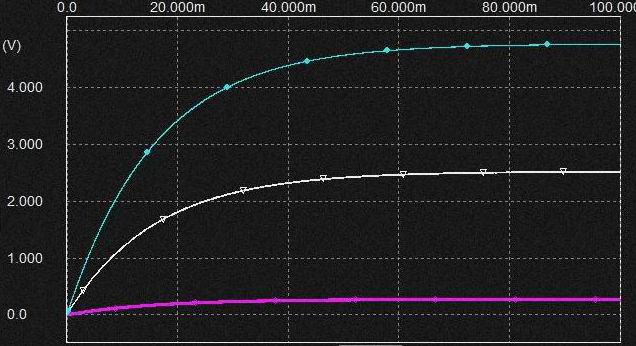
* LPF, HPFの位相特性(位相:リニア 周波数:対数スケール)
DCに近い周波数ではHPFは90度印加SIN波信号に比べて位相が遅れるのでそれが積分器に入ることによりLPF出力は-90+(-90)で180度位相が遅れることになります。 ここでこの積分器はOP AMPの積分器なのでそれがさらに180度反転してLPF出力は入力SIN波と同じ位相になります。
さらにこれがマイナスされて入力SIN波と加算されるのでDCに近い周波数ではHPF出力は0に近づくわけです。 --->位相差0の同じ振幅の信号を+,-する。
構成(回路)上からは印加される正弦波とLPFからの帰還信号は逆相でOPAMPに入力されるの ですが、積分器がループ内にあるためすべての状況でLPF出力が完全に負帰還されるわけではないわけです。
DCつまり増幅度が非常に大きくなるポイントではHP出力が0に近いわけなので必然的にLPF出力は印加SIN波と同位相でかつ振幅も同じに近づくわけです。 両者は別々の入力(+,-)に印加されますので完全に180度の位相差の負帰還に近くなるわけです。
|
このanalog 1次LPFの基本的な考え方としては、 積分器の 1/f特性を遮断領域の特性(カーブ)として利用して、通過領域に対しては 1/f特性が無効になって均一(GAIN=1)の特性を作るために負帰還を利用するということです。
GAINが大きければ大きいほど印加入力信号に対して出力を負帰還することで出力は1に近づく、すなわちGAINが1以上ある区間では出力特性は1に近づき、 GAINが1以下の区間では負帰還の効果があまり働かないので 1/f特性に近くなるという。 CR filterの場合は 遮断帯域の電流を一定化させることにより 1/Fの特性を引き出し、通過帯域はCap.の素の電流特性にすることで積分特性は相殺、上記の電圧のみの対応のfilterでは積分器出力電圧は積分特性そのものなので通過帯域を負帰還させることで平坦化します。 どちらも主要素の変化が大きくなる帯域に対して負帰還がかかる反応ということです。 |