Chapter Twenty Seven

第27話


今回はサウンドの圧縮方法のひとつであるμ法則（Mu-law)について書いてみよう。ITU-T Recommendations (CCITT) に定められているらしいが、仕様を書いた資料は有料なので手元にはない。さいわいComputer-Music-JournalにSUNがANSI-Cで書いたreference implementations（ccitt-adpcm.tar.Zの中のg711.c）があったので、これを参考にLabVIEWでプログラミングしてみよう。

さて、Mu-lawは電話で通信できる64kbpsを８bit×８kHzで実現することを念頭に考えられたフォーマットで、人間の聴覚が音の大きさに対して対数的に反応することを利用して音質劣化を押さえながらデータを圧縮する方式だ。このあたりの考え方は、Mario Malcangi Fall 1995 IEEE Computer Society Pressに説明されている。

Mu-lawは１６ビットから８ビットへの非可逆圧縮で、データが大きくなるにつれて代表値を取り出す間隔を対数的に広げていく。対数的にと言うと難しく考えてしまうが２進数で考えたときの数値の最上位ビットの位置をみると対数的なスケールにすることができる。
16ビットのビット列をb(15), b(14), ...., b(1), b(0)と呼ぶことにすれば、b(4)より大きなビットが全て０のときセグメントを０として、順次b(4)より大きなビットが立つ毎にセグメント値を大きくしていく。セグメントは３ビットで表現し、０から７のセグメントに分かれる。数値は上位４桁のみを使用する。正負をあらわすパリティを加えて８ビットで正負を含めて１３ビットの数値を表現する。
7
6
5
4
3
2
1
0
P
S２
S1
S0
Q3
Q2
Q1
Q0

例えば、13は２進数で1101だが、左にひとつづつシフトしていくと次のようになる。

Dec ビット列 セグメント 数値
13
0000000000001101
0
0110
26
0000000000011010
0
1101
52
0000000000110100
1
1101
104
0000000001101000
2
1101
208
0000000011010000
3
1101
416
0000000110100000
4
1101
832
0000001101000000
5
1101

以上はMario Malcangi氏の説明から理解したMu-lawの基本的な考え方である。
しかし、SUNのreference implementationsでは変更が加えられている。おそらくプログラムの書きやすさと16ビットから変換したときの音量の統一性からだと思うが、ファイルの互換性を取ろうと思うとreferenceに従わざるをえない。
reference implementationsでのおおまかな手順は次の通り。
(1) 16ビットデータの正負を判定する。
(2) 絶対値に0x84(0000000010000100)を加える。
(3) b(7)より大きなビットが全て０のときセグメントを０として、順次b(7)より大きなビットが立つ毎にセグメント値を大きくしていく。
(4) セグメント数＋３だけ右シフトし、0xFとのANDをとる。

結果としてb0,b1は無視されることになる。前に使った例をreference implementations方式にすれば以下のようになる。
Dec 0x84を加算後のビット列 セグメント 数値
13
0000000010010001
0
0010
26
0000000010011110
0
0011
52
0000000010111000
0
0111
104
0000000011101100
0
1101
208
0000000101010100
1
0101
416
0000001000100100
2
0001
832
0000001111000100
2
1110

実際のVIは比較的シンプルに書くことができる。C言語でのプログラムコードを逐次LabVIEWに移し換えることもできるが、効率があまり良くないことが多い。経験では、できるだけ配列の操作に持ち込んだ方が得だと思う。
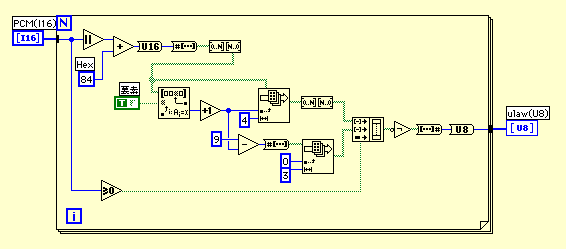
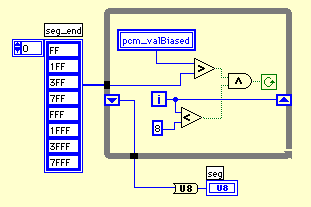SUNのreference implementationsからMu-lawの部分のみ引用させてもらってLabVIEWでそのままトレースした場合のダイアグラムと対比してみよう。

static short seg_end[8] = {0xFF, 0x1FF, 0x3FF, 0x7FF, 0xFFF, 0x1FFF, 0x3FFF, 0x7FFF};
static int search(int val, short *table, int size)
{
int i;
for (i = 0; i < size; i++) {
if (val <= *table++)
return (i);
}
return (size);
}


　
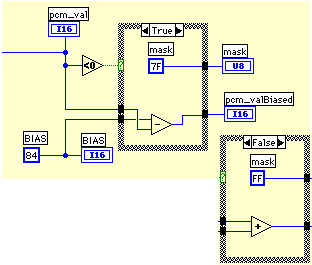#define BIAS (0x84) /* Bias for linear code. */
unsigned char linear2ulaw( int pcm_val ) /* 2's complement (16-bit range) */
{
int mask;
int seg;
unsigned char uval;
/* Get the sign and the magnitude of the value. */
if (pcm_val < 0) {
pcm_val = BIAS - pcm_val;
mask = 0x7F;
} else {
pcm_val += BIAS;
mask = 0xFF;
}

/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_end, 8);
/*
* Combine the sign, segment, quantization bits;
* and complement the code word.
*/
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
uval = (seg << 4) | ((pcm_val >> (seg + 3)) & 0xF);
return (uval ^ mask);
}
}


間違っているところもあるかも知れないが、LabVIEWでそのままワイアリングするとこんなところだろう。

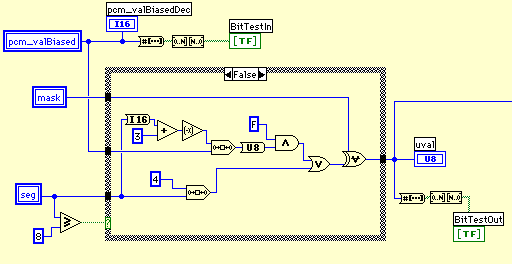
次回はどんなことをしようかな？
See you!


Nigel Yamaguchi
戻る