四則演算の最後となった除算VIについて説明しよう。
考え方として簡単なのは引き算を繰り返す方法だが、計算時間は繰り返しの回数(被除数と除数の比)に比例する。筆算方式の場合の計算時間は被除数と除数の桁数の差にだいたい比例するだろう。だから、VIをつくる手間はかかるが筆算の方法を選んだ方が良さそうだ。
そのための準備として、桁上げVIを作ることにした。U32n;Aをビット列と考えたとき、左シフトを繰り返し最大ビットが1になるようにするVIだ。
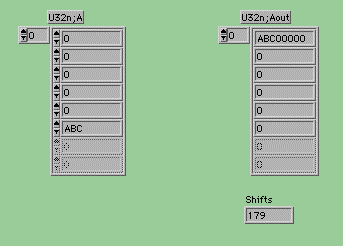
シンプルな考え方は、最大ビットが1になるまで左シフトを繰り返す方法だ。(Shift0.vi)
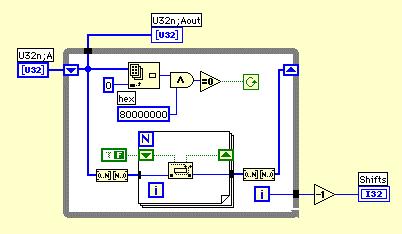
しかし、ビット列の先頭から0がたくさん続くときは、いっきにシフトした方が速そうだ。U32単位で、0がどこまで続くか調べて事前にシフトする方法を試してみよう。(Shift1.vi)
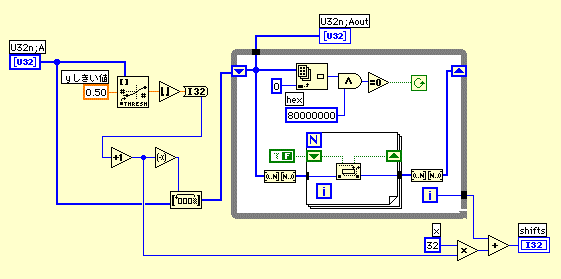
スレッショルド関数は遅いかもしれないから、Whileで回した方が速いかもしれない。(Shift2.vi)
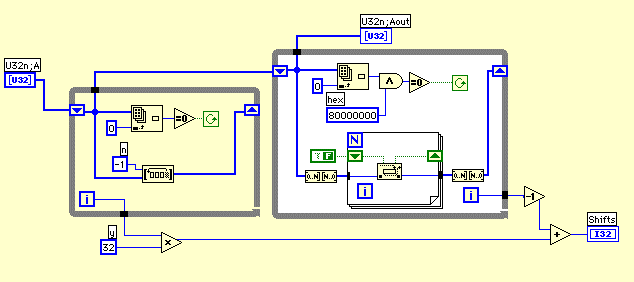
さあ、3つの方法を考えたが、どれが一番速いのだろうか?LV4のプロファイルで調べてみよう。
配列の上半分が0でそれ以下がランダムなU32nの時の動作時間
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
配列の全体がランダムなU32nの時の動作時間
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
このテストからShift1.viの方法が安定して速いことが分かったが、調べると入力の配列の要素が1の時にシフト数が変になるので、Shift2.viを使うことにした。標準のわり算の配置に合わせてフロントパネルに要素を配置した。
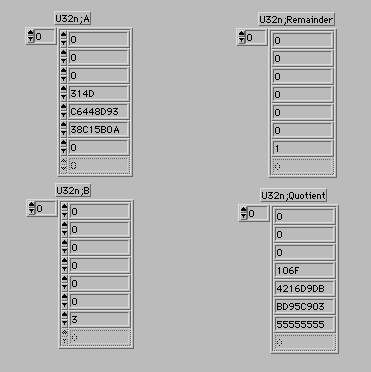
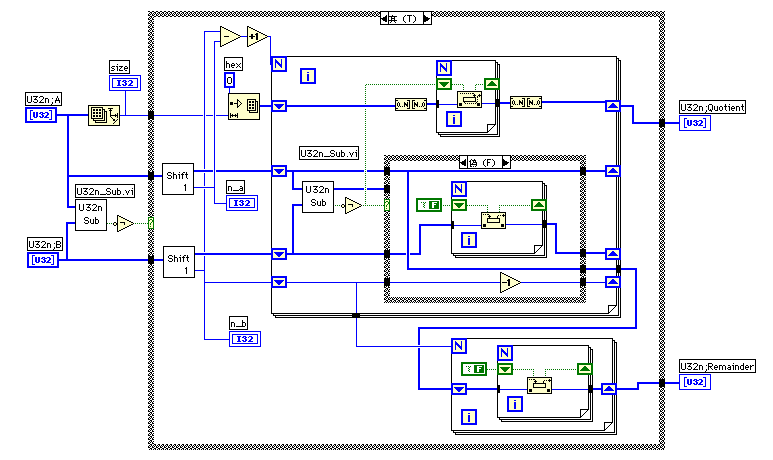
(1)A,Bともに先頭のビットが1となるようにShift1.viで左シフトを行う。A',B'としよう。
以上が大まかな計算の流れだ。これを書きながらバグチェックをしている状態だから、もっと頭が整理できれば簡単になりそうな気もするのだが、、、
See you!
Nigel Yamaguchi
戻る