Chapter Thirteen
第13話
-
今回でU32の暗号VIは最終回となる。
- まず、結果から見てもらおう。公開鍵となるNとeを入力し、通信文を"平文"に入れて実行すると暗号文が0〜Fに変換されて出力される。
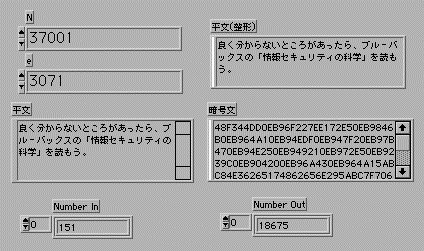
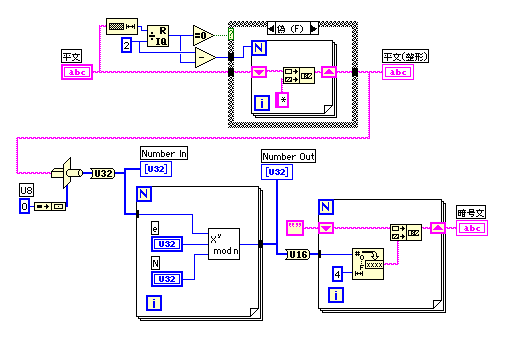
- ダイアグラムは、サブVIのおかげでシンプルになっている。
- 1バイト文字と漢字など2バイト文字に対応するため、文字数が2×nとなるように文字数の調節を行う。整形した文字列をU8配列に変換した後、U32に変換する。
- つまり、一生懸命作ったわりにはさみしい現実だが、1バイト単位で暗号化するということだ。その理由は前々回に説明してある。
- U8の入力をX^y mod Nで変換すると変数はU32でもU16の範囲の数値となる。これを16進の文字列に変換して暗号文として出力する。これではデータサイズが2倍になってしまうが、U32の制約のためだから今回はしょうがないと考えよう。
復号の場合は、公開鍵Nと秘密鍵dを入力し、通信文を"暗号文"に入れて実行する。
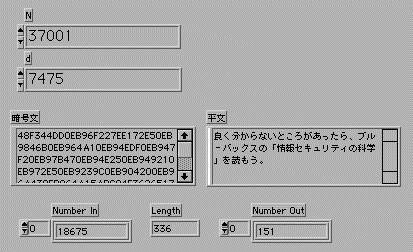
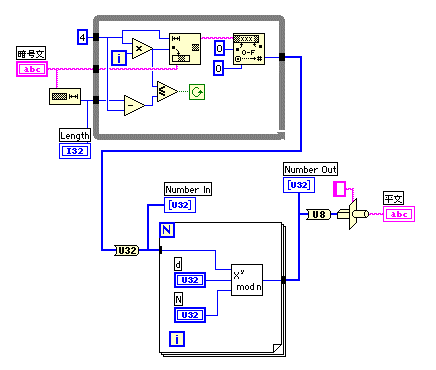
- 暗号文をU16相当の4文字ずつ切り出してU16数値に変換した後でU32に変換する。それをX^y
mod Nで変換し、さらにU8に変換した後で文字に変換することにより、平文をえる。
さて、不思議に思わないかい? いったいどんなマジックが働いて同じ関数X^Y
mod Nを使って公開鍵で暗号化したものを秘密鍵で復号できるのだろう。
- ところで念のために書くと、M mod Nは”MをNで割った余り”のことだ。この関数にはいくつかの便利な性質がある。
(a×b×c)mod N = ((a mod N)×(b mod N)×(c mod N)) mod N のように途中でmodを取っても同じ結果が得られる。これで、途中の積の計算が大きな数にならないように計算することができる。
- また、この関数には以下の「フェルマーの定理」という定理が知られている。
- 「任意の素数pと任意の整数m ( 1 < m < p ) に対して、
- m^(p-1) mod p = 1
- が成り立つ。」
- フェルマーの定理から、N が素数p, q の積で、L が(p-1) と(q-1) の最小公倍数のときに
- M^L mod N = 1が導かれる。
- (但し、 1 < M < p かつ1 < M < p )
Mが平文で、暗号化を公開鍵N, eで暗号化すると、暗号文Cは
- C = M^e mod N
- で作られる。これがC^d mod Nで平文Mに戻る様子を調べてみよう。
- 但し、「L とe が互いに素のとき1 = L*c + e*d となるc, d が存在する」という関係もこの中で使っている。
C^d mod N=(M^e mod N)^d mod N
- =M^(ed) mod N
- =M*M^(ed-1) mod N
- =M*M^(-Lc) mod N
- =M*(M^L mod N)^(-c) mod N
- =M*(1)^(-c) mod N
- =M mod N
- =M
以上の説明は、「情報セキュリティの科学」の解説に基づいたものであることを断っておこう。デフィーとヘルマンの公開鍵方式の実現をあきらめかけた3人(リベスト、シャミア、エーデルマン)が見つけだした巧妙な仕掛けだ。すごいね。
See you!
Nigel Yamaguchi
戻る



