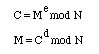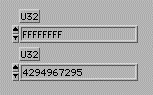Chapter Eleven

第1１話

今回は、予告通りU32でRSA暗号の動作を追ってみよう。
公開鍵と秘密鍵の決定手順はそんなに面倒ではない。コンパクトに書くと次の五つの手順からなる。
１）素数を二つ選ぶ。p, q としよう。
２）N = p * q を計算する。
３）(p-1) と(q-1) の最小公倍数L を求める。
４）L と互いに素となるe を選ぶ。
５）1 = L*c + e*d となるd を求める。
公開鍵はN,e で、秘密鍵はdとなる。
平文をM、暗号文をCとすると、暗号化と復号化は公開鍵と秘密鍵を使って以下のように行われる。Mは文字をASCIIコードなどの数値に変換し、ある長さのブロックごとに取り出したものとして考える。

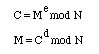
さて、U32は符号無し３２ビット整数だが、この中で表せる最大の整数はいくつだろうか？　形式を16進数に変更してffffffffを入力して、また十進数に戻すと、頭を使わなくても簡単に結果が得られる。

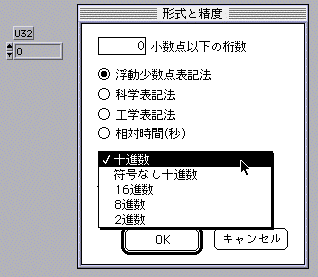
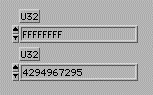
この通り、たかだか１０桁の数字しか扱うことができない。暗号化と復号化での累乗計算をまともに行うとすぐに１０桁を越えてしまう。しかし、剰余計算の性質を使えば数字が爆発しないようにうまく計算できる。
下のブロック図は悪い例だが、シフトレジスタのU32がすぐに（23^8程度の数でも）オーバーフローしてしまう。

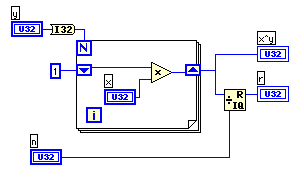
つぎの例はこまめにModを取ることにより、オーバーフローが起きにくいダイアグラムにしたものだ。x^yのyを２進数表現（数値からブール配列への変換）し、Trueの場合x^(2^k) Mod Nを計算するSubVI(図の下部）を動作させている。Falseのときは（図がないが、）何も実行されない。ついさっきまでバグ取りをしていたものだから、まだ残っているかもしれないので、要注意。

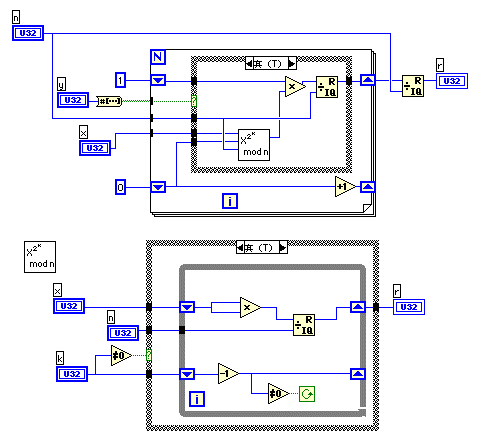
公開鍵N,e と秘密鍵dを決めればこのVIで暗号化、復号化の計算ができる。次回はN,e,dを決めるVIを作ってみよう。
See you! Nigel Yamaguchi 戻る