Chapter Ten
第10話
-
”次回はどんなふうに現代の暗号に入っていくのだろう。”と、企画の無謀を知った上での話だ。始めに参考書を紹介しておこう。
「PGP 暗号メールと電子署名」オライリー・ジャパン発行、オーム社発売
- 「情報セキュリティの科学」(ブルーバックス)講談社発行
- 「素数の不思議」(ブルーバックス)講談社発行
- 「暗号理論入門」共立出版
あくまでもLabVIEWで遊ぶための題材だから、本格的な暗号物だとは思ってはいけない。だいいち、俺は暗号のプロでも、CIAのエージェントでもない。
- 従来の暗号では、複数の人間が独立して暗号をやりとりする場合、組み合わせの数だけの鍵が必要になる。つまり、n人ならn*(n-1)/2の鍵を秘密裏に取り決める必要がある。1975年、スタンフォード大学のDiffieとHellmannが「メッセージをある鍵で暗号化して別の鍵で複合化するマルチユーザー暗号を実現できるはずだ」という、アイデアを提示した。全ての人が自分の望まない人、組織に対するプライバシーの確保を確信できる通信システムの概念が生まれたのだ。
この概念は多くの研究者の注目を集めたが、実現手段の発見は容易ではなかった。
- MITのRivest,Shamir,Adelmanがたどり着いたのは、「素数の積を計算するのは容易だが、積をもとの素因数に分解するのは時間がかかる」、という経験則を応用したものだ。
もっとも10桁ぐらいの素因数分解ではそんなに時間はかからない。たとえばU32の範囲で扱えるもっとも大きな素数の積は65519と65521のかけ算でできる4292870399だが、素因数分解は簡単なVIで0.2秒ぐらいで分解することができる。ちょっとはみ出してしまうが素因数分解をするVIのダイアグラムを紹介しよう。
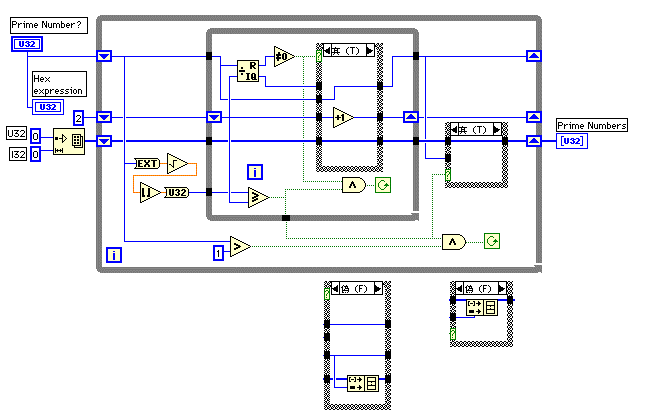
- 分解しようとする数(P)を2から√Pまで順番にわり算を行い、割り切れる数を探していく方法だ。Pが大きな素数の積でできていると、計算時間もかかる。
- U32の範囲で、ビット数が増加すると計算時間が指数的に増加する様子を見てみた。横軸がビット数、縦軸が計算時間だ。
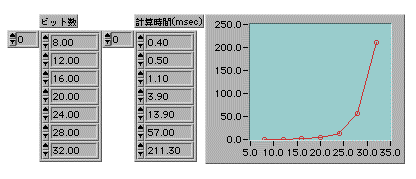
- 計算に使った数は下の表のものだ。「素数の不思議」には20ページも使って1から10万の間の素数が書いてある。はじめに読んだときはページの水増し策かと思ったが、役に立つこともあるんだな。
| ビット数 |
積 |
素数1 |
素数2 |
| 8 |
143 |
11 |
13 |
| 12 |
3599 |
59 |
61 |
| 16 |
60491 |
241 |
251 |
| 20 |
1040399 |
1019 |
1021 |
| 24 |
16744463 |
4091 |
4093 |
| 28 |
268140589 |
16369 |
16381 |
| 32 |
4292870399 |
65519 |
65521 |
- さて、この計算速度で128ビットの場合を外挿するなら10^200年ぐらいかかってしまうだろう。これは、PM7500/100とLV4で計算した場合で、現在の最高速の計算機が束になって計算してもすぐには解けないようにするには1024ビットの鍵を使うのが適当らしい。
U32 では暗号遊びにもならないことが分かったが、次回は暗号化の手順を知るために、U32でトレースしてみよう。
See you!
Nigel Yamaguchi
戻る

