AMI用語集
![]()
AMI用語集
音列技法
(独)Reihentechnik
|
音列技法は、アーノルト・シェーンベルク(Arnold Schoenberg, 1874-1951)によって1920年代初頭に創始され、それ以後彼とその弟子アルバーン・ベルク(Alban Berg, 1885-1935)やアントーン・フォン・ヴェーベルン(Anton von Webern, 1883-1945)らの創作において最も重要な役割を果たした作曲技法である。彼らはしばしば「新ヴィーン楽派」という名のもとにまとめられる。 これを一言で云えば、後段で詳説する〈音列〉Tonreihe を用いて作曲すること、もっと云えば、音列のみによって作品全部を構成することである。この方法は1オクターヴ内の12音を等価なものとして扱うため、「12音技法」と呼ばれることもあるが、この名称の場合、同時期に、音列技法とは異なるアプローチでこれを考えたヨーゼフ・マティアス・ハウアー(Josef Matthias Hauer, 1883-1959)などの流儀をも含めることになるであろう。 【音列とは】 音列とは、何か。 例としてシェーンベルクの「ピアノ組曲」(作品25,Universal Edition刊)の前奏曲の譜面を見てみよう。冒頭の右手のメロディを追っていくと、(異名同音に関しては、特に区別を必要としない限り嬰音での表記に統一する、) E, F, G, C#, F#, D#, G#, D, B, C, A, A#……[1] 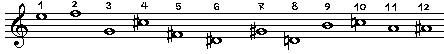 の順で12の音が現れるのがわかる。これがこの前奏曲、延いてはこの組曲全体を支配している基本の音列である。彼らの音列技法とは、一つの音列の変形や移動によって、一つの作品全体を形成する技法を意味する。 ではその「変形や移動」は、具体的にはどういうやり方でなされているだろうか。 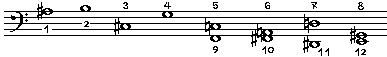
このように、音列は、全体の音高をそっくり別の音に平行に移して用いることができる。これを移高 transposition (この語は、従来の音楽の理論では「移調」と呼ばれる)と呼んでおこう。また、[2]の例でも判る通り、一つの音列は必ずしも継時的に現れる必要はなく、途中で複数のグループに分けて、音列の中の他の音と和音を形成することもできる。他の音列の音とも当然重なりうるわけで、実際、[1]と[2]の音列は曲の冒頭で同時に鳴らされている。 移高以外にも、音列技法にとって重要な変形の方法がいくつかある。 逆行とは、音列の中に音が現れる順番を全く逆にひっくり返すことである。 A#, A, C, B, D, G#, D#, F#, C#, G, F, E という音列ができるが、これをいま試みに、E音から始まるように移高させてみよう。すると、 E, D#, F#, F, G#, D, A, C, G, C#, B, A#……[3] となる。 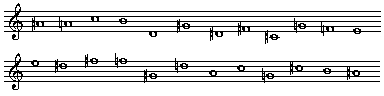
ここでシェーンベルクの前奏曲の楽譜に戻り、5小節目を見てほしい。4拍目までの部分は全体が3声に分かれているが、低声が音列[3]の1〜4番目の音、中声が5〜8番目、そして高声が9〜12番目の音を鳴らしているのが判るだろう。このように、移高や逆行、分割、そして次に述べる反行といった方法を同時に用いることも可能である。 反行の説明はもう少し複雑になる。一言で云えば、音列の中の音程の上下運動を対称的に逆さまにすることである。 A#, A, G, C#, G#, B, F#, C, D#, D, F, E……[4] 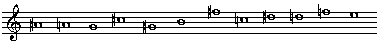
前述の前奏曲の中にも反行型の例はいくつかあるが、いずれも少し繁雑な操作が加えられているので、比較的単純に見つけられる、第2曲「ガヴォット」第2小節目の例を指摘しておこう。3拍目から始まる右手のメロディは、音列[4]の第8音目までを、少し遅れて入る左手は9音目から後を鳴らす(12音目の後にもう一度9音目まで逆行する楽句が付け加えられているが)。 もちろん反行型の逆行型 inversive retrogradation も用いることができる。また、今までの曲の中での使用例を見ても判るとおり、音列の中の一音、あるいは数音を繰り返して使うことも、時としてある。また、2〜4音ほどの音の小グループのみを逆行させたりもする。 このように、実際に曲の中で音列が使われる際の方法は、かなりの自由さを許容している。しかし、この組曲全体がただ一つの音列から作られているのと同じように、音列による作曲は、たとえ30分を越える大作であろうとも、基本音列を一つに限ることを原則とする。一つの音列から12種類の移高型が作られ、それぞれの逆行型、反行型、逆行反行型の、計48種類の音列が派生する。これらを切り刻んだり重ねたりして、様々に料理するわけである。 【なぜ音列なのか】 では何故彼らは、わざわざこのような一見煩雑とも云える過程を経て、曲を作ることにしたのだろうか。それについて少し考えてみよう。そのためには、この技法を用い始める前の時期の、彼らの作風について一顧する必要がある。 音列技法を開始する10年と少し前に、彼らはいわゆる「自由な無調」という作風に辿り着いた。 そのように音楽を導いていくためには、ある特定の調を不必要に想起させるようなメロディや和音は、極力避けられることになる。例えば完全5度と3度を持つ三和音などは、まず用いられない。 ここで重要になるアイテムは、調性音楽では解決を必要とする非和声音を含んだ形でしか用いられなかった、長・短7度ないし9度などの音程や、増三和音、4度累積和音などである。 「音列」というアイデアが有効性を持ってくるのは、この局面においてであろうとまずは考えることができる。音列はオクターヴ内の12個の音を重複せずに1回ずつ用いて作られるので、これを基礎に作曲すると、オクターヴを持たないパッセージが比較的楽に作れるというメリットがある。 ここで更にもう少し問題を遡ってみることもできよう。即ち、何故彼らが「無調」に向かう必要があったのかという問題である。これについてはまた項を改めることにしよう。(10/06/01) |
copyright 2000-2002 by ARAO Gakuji
aragak@aragak.com