Abstract
24節気の定め方には平気法（または恒気法）と定気法の2種類がある。平気法は、1太陽年を単純に24等分したものであるが、定気法は「ケプラーの法則」を応用した複雑な計算が必要である。 　現在、多くの暦、カレンダーなどに掲載されている24節気は定気法によっている。しかし日本の公式な暦に定気法が採用されたのは江戸時代末期の天保暦だけで、それ以前の千年以上にわたって平気法が用いられていた。 　平気法によって節気を求め、定気法とどれくらい違うかを確かめて見た。また「ケプラーの法則」を用いて定気法による節気を誤差数分以内で求める計算アルゴリズムを掲載する。

序

平気法と定気法

平気法による試算

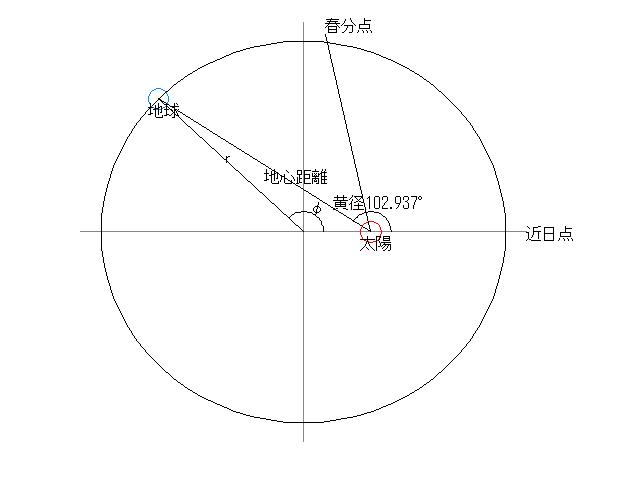
定気法−１　太陽の黄径から地心距離を求める

定気法−２　翌日の黄径を求める

誤差について

天球、黄道、黄径

序
　多くの暦やカレンダーには「24節気」が載っている。これは古くから季節の節目とされてきたもので、特に立春、立夏、立秋、立冬は各々春夏秋冬の始まりとするのが伝統的な考え方である。
　さて、この24節気というのは、簡単に言えば1太陽年を24等分したものである。江戸時代まで用いられて来たいわゆる「旧暦」は1朔望月を1箇月とするものであるから、12箇月では354日程度となり、1太陽年よりかなり短い。このためときに「閏月」を設けて1太陽年に近付けるわけであるが、そのときに24節気が用いられる。これに関する詳しい解説はたとえば海上保安庁海洋情報部のページの「こよみあれこれ」に見られるが、つまりは太陰暦に太陽暦の要素を組み入れるために考案されたもの、と考えて差し支えなかろう。実際、旧暦というのは「太陰太陽暦」と呼ばれる。

平気法と定気法
　ところで、24節気の定め方には２つのものがある。
　ひとつは「平気法」というものである（上記の海上保安庁海洋情報部のページでは「恒気法」となっているが、本稿では平凡社世界大百科事典に従い、「平気法」を採用する）。これは1太陽年を春分点を起点として単純に24等分するものである。
　1太陽年は、理科年表によれば365.2422日である。「4年に一度の閏年」なら365.25日となって、やや長すぎる。それで現在日本をはじめ多くの国で採用されている「グレゴリオ暦」では、閏年は400年に97回となっている。これなら1年は365.2425日、大分近いが、それでも1万年では3日ずれる。「そんな先のこと誰も知っちゃあいない」。
　ともかく、平気法ではこの1太陽年を単純に24等分するのであるから、たいして難しいことはない。日本の昔の暦は、江戸時代末期の「天保暦」を除いてすべて平気法であった。
　もうひとつは「定気法」という。
　太陽が天球上を1年かかって1周する経路を「黄道」と言い、黄道上で春分点を起点として計った角度を「黄径」と言うが、定気法では太陽の黄径が0°、15°、30°、45°・・となった時を24節気とする。
　一見これは平気法と同じことのように思えるが微妙に違う。何故かというと、地球が太陽の周りを公転している軌道は厳密には円ではなく楕円である。そして太陽から地球までの距離（地心距離）はほんの僅かながら変化する。そして「ケプラーの第2法則」というのがあって、同じだけの黄径（たとえば15°）を進むのに太陽までの距離が近いときには速く、遠いときには遅くなるのである。定気法ではこの効果まで考えるので、節気の間の時間は一定ではない。
　ちなみにこの法則は、ニュートン力学では「角運動量保存則」として一般化される。フィギュア・スケートで、はじめ手足を伸ばしてゆっくり回転し始めたのが、手足を縮めると急速に回転する、まさにあれと同じことを地球もやっているのである。
　さてこんなかなり複雑な定気法であるが、既に隋の時代に始まっているという。ケプラーより1000年ほども昔である。ケプラーの法則どころか、地動説も知られていたかどうか。これってすごくない？
　日本では、江戸末期の「天保暦」だけがこの定気法を採用している。そしてこれは明治の新暦採用までのわずか29年だけ使われたにすぎない。定気法は日本の文化に馴染んでいるとは言い難いのである。
　しかしながら、現在発行されている暦、カレンダーの多くに掲載されている節気はこの定気法に準拠したものである。たとえば「神宮館暦」。筆者は占いや迷信の類にはたいして興味はないので、買ったことがなかったのだが、これを書くのに資料として一番安い300円のを買ってみたら、たとえば立春は「太陽の黄径315度のとき」とされ、その時刻まで、 海上保安庁海洋情報部のものと同じである。平気法などの別の値を載せれば、それなりの価値はあるだろうに。

平気法による試算
　2003年3月21日10:00　（春分点）を起点として1年間の節気（立夏、夏至、立秋、秋分、立冬、冬至、立春）を平気法で求めてみた。1太陽年を365.2422日としている。「天文年鑑」（誠文堂新光社）による定気法の値と比較すると、立秋、秋分、立冬などは3〜4日も違ってくる。

定気法−１　太陽の黄径から地心距離を求める
　定気法の計算を行なうためには、太陽の黄径から地心距離を求める必要がある。
　地球から見て太陽は天球上の一定の道「黄道」を動いている。黄道上で春分に太陽が居る位置「春分点」を起点として測った角度が「黄径」である。
　地動説の観点で考えると、地球が太陽の周りを回っているが、その軌道上で春分に地球が居る位置が春分点、そこから測った角度が黄径である。ところで地球の軌道は厳密には円ではなく楕円であるから、太陽から地球までの距離「地心距離」は地球の居る位置、つまりは黄径によって変化する。

　地球の軌道は楕円であるから、その中心から長軸方向にｘ、短軸方向にｙをとれば、軌道は次の方程式を満たす。

＝１　　　　　　　　　　(1)

　ここで　ａ：長軸半径
　　　　　ｅ：離心率（０＜ｅ＜１）
　この式はｘ軸から（ｘ，ｙ）点への中心角φを用いて次のように書ける。

		ｘ＝ａ	ｃｏｓφ	(2.1)
		ｙ＝ａ		ｓｉｎφ　　　　　　　　　　(2.2)

　太陽はこの軌道の中心から長軸の正方向へａｅの所、つまり（ａｅ，０）にある。（ａ，０）が近日点である。黄径をΦ、地心距離をＲとすると、

		Ｒｃｏｓ（Φ＋180°−ΦP）＝ｘ−ａ	ｅ＝ａ（ｃｏｓφ	−ｅ）	(3.1)
		Ｒｓｉｎ（Φ＋180°−ΦP）＝ｙ＝ａ		ｓｉｎφ	(3.2)

　ただし近日点の黄径をΦ_Pとする。
　(2.1)(2.2)(3.1)(3.2)から、Ｒ，φに関して以下の式が得られる。

ｃｏｓ（Φ＋180°−Φ_P）＝０のとき
　　ｃｏｓφ＝ｅ　　　　　　　　　　(4.1)
　　Ｒ＝ａ（１−ｅ²）　　　　　(4.2)

ｃｏｓ（Φ＋180°−Φ_P）≠０のとき

ｔａｎ（Φ＋180°−ΦP）＝Ｓ＝

(4.3)

または

ｃｏｓφ＝

(4.3')

　　Ｒ＝ａ（１−ｅｃｏｓφ）　　　　　　　　　　(4.4)

　これらの式により、黄径Φから（ｃｏｓφを介して）地心距離Ｒを求めることができる。
　(4.3')の±は

近日点の反対側（90°＜Φ＋180°−ΦP＜270°）のとき	−
それ以外のとき	＋

である。

　下のフォームでは、上記の式により黄径から地心距離を求めることができる。ただし
　　ｅ＝0.01671
　　Φ_P＝102.9889°
としている。
　ａは、1（AU：天文単位）または 149597870(km) 　から選ぶことができる。

黄径° (AU) (km)

定気法−２　翌日の黄径を求める
　ある日の黄径から「ケプラーの第2法則」によって翌日の黄径を求めることができる。
　「ケプラーの第2法則」はニュートン力学における「角運動量保存則」と同じものである。以下では時間微分を ' で表わす。つまり

Φ'＝

　「ケプラーの第2法則」は
　　Ｒ²Φ'＝Ｃ　（一定）　　　　　(5)
　定数Ｃは、これを時刻０≦ｔ≦Ｔで積分した式から

Ｃ＝

　Ｔとして1太陽年をとれば、

Ｃ＝

　一方、(3.1)(3.2)から

Ｒ2ｄΦ＝ａ2

（１−ｅｃｏｓφ）ｄφ

　また
　　０≦Φ≦２π　に対して　０≦φ≦２π
　したがって

Ｃ＝

(6)

　黄径の単位を°、時間の単位を日、地心距離の単位をAU（天文単位）とすれば、
　Ｔ＝365.2422（日）、ａ＝１(AU)
であるから、

Ｃ＝

＝0.98551（°AU2／日）　　　(7)

　翌日の黄径を求めるために、(5)を差分化する。つまり、当日の黄径をΦ₀、翌日のものをΦ₁として、Φ'を
　　Φ₁−Φ₀
で近似する。このとき(5)より

Φ1＝Φ0＋

(8)

　これを計算するためには右辺の１／Ｒ²を決める必要がある。簡単な考察によってこれは１／（Ｒ₀Ｒ₁）とするのが精度が良いことがわかる。ただしＲ₀は当日の地心距離、Ｒ₁は翌日のそれである。
　Ｒ₀は(4.1)〜(4.4)を用いてΦ₀から求めることができるが、Ｒ₁はΦ₁が決まらなければ求められない。そこで、Ｒ₁の第０近似としてＲ₀を用い、Φ₁の第０近似Φ₁⁽⁰⁾を求める。

Φ1(0)＝Φ0＋

　これを用いてＲ₁の第１近似Ｒ₁⁽¹⁾を求め、Φ₁の第１近似Φ₁⁽¹⁾を求める。

Φ1(1)＝Φ0＋

　以下順次第２近似、第３近似・・を求めることも可能である（事実上第１近似までで充分）。

翌日の黄径を求める。 当日の黄径°

　これを順次繰り返せば、ある日（たとえば春分）から後の毎日の黄径を求めることも原理的には可能である。そして黄径が特定の値（45°，90°，・・・）を超える日が節気（立夏、夏至、・・・）である。
　この方法で2003年の春分から1年間の黄径を求めてみた。黄径は日単位で求め、時分は線形補間で求めたが、正しい値との誤差は数分以内である。


誤差について
　ここの計算では節気の時刻は線形補間で求めている。すなわち、節気の黄径をΦ_s、時刻ｔ₀における太陽黄径をΦ₀、ｔ₁におけるそれをΦ₁として、
　　Φ₀≦Φ_s≦Φ₁
である場合、節気の時刻ｔ_sは

ｔs＝ｔ0＋Ｄ

(9)

　ここで
　　Ｄ＝ｔ₁−ｔ₀＝24時間

　しかし実際にはケプラーの法則(5)が成り立つのだから、むしろ次のような補間が正しいであろう。

ｔs＝

(10)

　ただし

Ｑ0＝

(11.1)

Ｑ1＝

(11.2)

　これらの積分は以下のように近似できる。

Ｑ0≒

（Ｒ02＋Ｒ0Ｒs＋Ｒs2）（Φs−Φ0）　　　(12.1)

Ｑ1≒

（Ｒs2＋ＲsＲ1＋Ｒ12）（Φ1−Φs）　　　(12.2)

ただし、Ｒ₀、Ｒ_s、Ｒ₁は各々黄径Φ₀、Φ_s、Φ₁に対する地心距離である。
　この(10)式による補間も試みたが、結果は以前の(9)式のものとほとんど変わらなかった。すなわち、誤差は補間方法によるものではない。

　他に考えられる誤差要因としては、月の存在がある。一般に月は地球の周りを公転していると言われるが、より厳密に言うと、月と地球がその両者の共通重心の周りを公転しているのである。そして月と地球の全体が太陽の周りを公転している。したがって上に求めた節気の時刻は、月と地球の全体つまり共通重心に対するものである。地球はこの共通重心からいくらか離れた所にある。どのくらい離れているかというと、月と地球の質量比は約 1:100 であるから、共通重心から地球までの距離は月〜地球間距離の 1/00 程度と見積もることができる。月〜地球間距離は約38万kmであるから、共通重心〜地球は3800km程度である。
　一方、地球〜太陽間距離は約1億5000万km。これが（太陽の周りの）公転軌道の1ラディアン（約57°）に相当する。地球の公転は1日に1°弱（360°／365日）であるから、
　　1億5000万km÷57°≒263万km／日
　　　　　　　　　　　≒11万km／時間
　　　　　　　　　　　≒2000km／分
　したがって、共通重心〜地球の距離は公転時間の2分程度に相当する。これは今回計算の誤差とオーダー的には一致する。
　しかしながら、誤差要因をこれに帰するなら、新月、満月（太陽、地球、月がほぼ一直線）には誤差が小さく、上弦、下弦（太陽〜地球に対して月がほぼ直角）では誤差が大きいといった傾向が見られるはずであるが、今回の誤差と月齢の関係はあまり明確ではない。

　24節気は一太陽年＝365.2422日を24等分したもの、あるいは黄径が0°、15°、30°、・・になる時であるから、
　　春分＝前年の春分＋365.2422日
　　（以下同様）
として求めることも可能と考えられる。しかしこれをやってみると最大10分程度の誤差が生じて、あまり精度は良くない。原因は不明。

天球、黄道、黄径
　「神宮館暦」の二十四節気の説明にはこうある。

太陽が春分点を出て再び春分点に達するまでを黄径三百六十度とします。周天三百六十度というのはこのことです。これを二十四等分した位置にそれぞれの節気を配して、１ヵ年の気候の推移を知るようにしたものです。

　わかったようなわからんような。まあ、易占いを主眼とする本ではこの程度の大雑把な説明でも事足りるのかもしれない。しかし、24節気を科学として理解するためにはもうちょっと正確なところを知る必用があるだろう。

天球
　星空、というより現代人にはプラネタリウムを思い浮かべるほうが分かり易いかもしれない。あれはドーム型のスクリーンに星空を映し出す装置である。そのようなドームの屋根つまり球面があって、そこに星が貼り付いていると考える。これを天球と呼ぶ。そんな天球は実際にあるわけではないが、昔の人は実際にあると考えたかもしれない。
　地球の表面には緯度、経度を考えるが、天球にも同様のものを考える。これを赤緯、赤経と呼ぶ。赤緯90度は「天の北極」で、このすぐそばにあるのが北極星である。他の全ての星の位置も赤緯、赤経で表わせる。そして太陽、月と惑星を除く「恒星」の赤緯、赤経は変わらない。つまりこれら恒星は天球の上で不動である。そして天球は天の北極と天の南極（赤緯-90度）を軸として24時間（正確には23時間56分）で1回転する。いや実際には地球が自転してるんだが、地球から見れば天球のほうが回転してるように見える。

黄道
　さて、恒星以外の太陽、月、惑星なんかは天球に貼り付いてない。太陽について考えると、地球は太陽の周りを1年かけて公転してるんだから、地球の位置は昨日と今日では違う。これを地球から見ると、太陽のほうがそのずっと向こうの恒星つまり天球に対して動いたように見えるわけだ。天球は23時間56分で1周する。つまり、地球の天球に対する自転周期は23時間56分だが、その間に地球は太陽に対して動くから、地球上のある点が太陽のほうを向いてから、再び太陽のほうを向くまでには24時間かかる。これが1日として認識される。だから、太陽は天球上を1日に時間にして4分に相当する分移動する。
　このように太陽が天球上を動く道筋というのは決まっていて、これを黄道と呼ぶ。黄道は天の赤道（つまり天球上に描いた赤緯0度の線）に対して23.5度ほど傾いていて、2箇所で赤道と交差する。この交差点が春分点と秋分点で、太陽が春分点にある時が春分、秋分点にある時が秋分である。

黄経
　太陽は天球上を動いているわけだから、無論その位置は赤緯、赤経で表わすことができる。しかし、上に述べたように太陽は必ず黄道上にいるんだから、黄道に沿ったものさしで位置を表わすほうが便利ということは容易にわかるだろう。このものさしを黄径と呼ぶ。黄径の基準（黄径0度）は原理的にはどこに取っても良いわけだが、歴史的な経緯で春分点に取ることになっている。
　春分点を黄径0度に取って、そこから夏至点つまり黄道の赤緯が23．5度になる方へ向かって黄径が増えて行き、さらに秋分点、冬至点（黄道の赤緯が-23．5度）を通って、再び春分点に戻る。1周した時の黄径は無論360度になる。これで「神宮館暦」の説明の「黄径三百六十度」、「周天三百六十度」という意味がわかると思う。

平気法と定気法