視覚の誘導場の工学的応用

視知覚の場による形らしさ検討

●　まえがき

　図形がどのような状態の時に，形やまとまりとして見えるかについて，ゲシタルト心理学等多くの研究はあるが，なぜ形として見えるのかは，十分説明できていない（行場，1995）．最近，図形の形やまとまりを工学的に扱い，文字の読み易さ，文書レイアウトの良さなどの感性を定量評価する手段として，視知覚の場が注目されている（長石，2014）．視知覚の場は，横瀬が提案した，図形の周りに静電場のような場を仮定し，パターン認知などの視知覚現象を説明する心理学的概念である（横瀬，1986）．
　横瀬は場の分布が，文字の類似性，錯視図形の解釈など，我々の物の見方，感じ方と関連すると考えた（横瀬，1986）．横瀬は場の分布が，文字の類似性，錯視図形の解釈など，我々の物の見方，感じ方と関連すると考えた（横瀬，1986）．
　視知覚の場について，内山は，いろいろな図形の場の強さを分析し，図形の周りの場の広がりが，視知覚の成立過程と関連があること，主に図形の輪郭線近くの場の分布が，できるだけ丸く円のようになっていると，図形が形やまとまりとして見えるとの考えを示している(内山，1967；内山，1968）．
　一方，長石は，図形の輪郭線による視知覚の場の計算方法を提案（長石，1996），場の分布が丸く円になっている程度を，場の分布の複雑度で定量化し，複雑度が文字列の読み易さ（長石，1998），フォントやパターンの印象の強さ（長石，2003），フォントの読み易さ（長石，2005）を評価できることを報告している．そして，場の分布の複雑度が場の強さで異なることに着目，場の分布の複雑度を場の強さのシグモイド関数で表し，文書のレイアウトの良さ（長石，2011），顔表情の違い（長石，2014）を説明できることが報告されている．
　これまでの長石の研究は，様々な図形について，視知覚の場の複雑度で感性的な定量評価が可能か追求したものだが，内山の視点のように，視知覚の場は，図形が形やまとまりとして見えるための要因になっているかという検討はされていない．視知覚の場は，様々な図形について，感性的な評価の可能性が示されているので，場の複雑度は図形が形やまとまりとして見える上で関連が高いと考えられる．
　そこで，本研究は，視知覚の場の分布の複雑度が，図形の形やまとまりとして見える上で関連があるか確かめるため，まず，無意味図形など簡単な図形について，場の強さによって複雑度がどのように変化するか調べ，形やまとまりとして見える場合，シグモイド関数のようになることを示す．次に，単純な眼，口，鼻，眉の部品からなる顔図形について，全ての部品が揃っていない顔らしくない図形から，部品を増やした顔らしい図形に変化させて，シグモイド関数で顔らしさが評価できるか検討し，視知覚の場の複雑度の変化の仕方が，図形が形やまとまりとして見える上での要素になり得るか考察した．

●　簡単な図形における複雑度の変化

　まず，形として見える図形の視知覚の場の複雑度の変化が，場のポテンシャル値のどのような関数となっているか，簡単な図形で観察を行った．図形画像は，白黒２値のディジタル画像で，64×64ドットの矩形に入るように拡大または縮小させて，64×64ドットの大きさのパターンの領域を含む128×128ドットの範囲で視知覚の場を計算する（長石，1996）．そして，各パターンの複雑度を，場の強さ0.01（視知覚の場の等ポテンシャル面が画像の外枠に接触しない限界）から0.399（文字画素の近傍付近）まで，0.001ステップで計測する．

（無意味図形）

　簡単な図形として，閉じた輪郭図形で，形態的に無意味で日常物体を容易に連想できない無意味図形（遠藤・齋木・中尾・齋藤，2003）100個について観察を行った．図1は，そのうちの10個について，縦軸に場の複雑度，横軸に場のポテンシャル値をとったグラフで，グラフ中の図形は無意味図形を示す．図1の例も含め，無意味図形において，複雑度はポテンシャル値に対し単調増加する傾向が見られ，シグモイド関数のような特徴をもった変化は見られなかった．

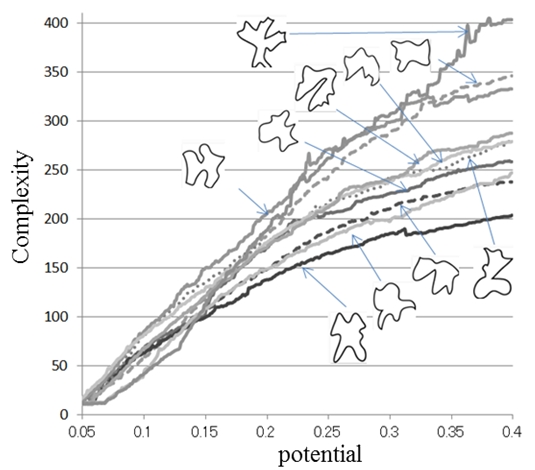
図1　複雑度の変化：無意味図形（遠藤・齋木・中尾・齋藤，2003）

（線図形）

　単純な線分で構成された線図形（Lupker，1979）について観察を行った．図2は，縦軸に場の複雑度，横軸に場のポテンシャル値をとったグラフで，グラフ中の図形は線図形を示す．図2から，「／」「｜」などの図形は，複雑度はポテンシャル値に対して単調増加しているが，「×」「T」など記号に見える図形は，シグモイド関数の特徴である平坦部と立ち上がりの変化が見られる．

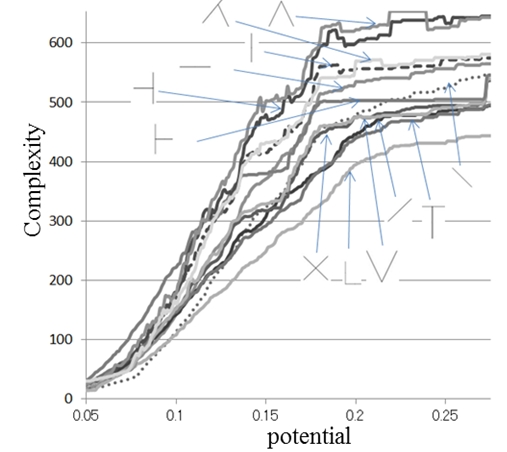
図2　複雑度の変化：線図形（Lupker，1979）

（単純図形）

　単純図形（長石，2003）について観察を行った．図3は，縦軸に場の複雑度，横軸に場のポテンシャル値をとったグラフである．図3から，円，正六角形，正方形，正三角形について，複雑度はポテンシャル値に対して，単調変化ではなく，シグモイド関数の特徴である平坦部が見られる．
　以上のように，簡単な図形において，何の形か認識できる図形の場合，複雑度はポテンシャル値のシグモイド関数に近くなると考えられる．

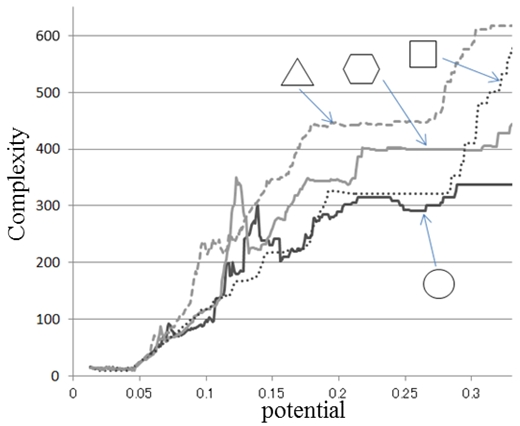
図3　複雑度の変化：単純図形（長石，2003）

●　シグモイド関数による顔らしさの検討

　形かどうか判別できる図形の場合，複雑度はポテンシャル値のシグモイド関数になっているかどうか確かめるため，パターンの構成を変えて，形かどうかわからないパターンから，徐々に形らしく見えるパターンに変化させたとき，場の複雑度の変化がシグモイド関数になるか調べた．

　検討パターンとして，眼，口，鼻，眉を部品とする顔図形を用い，(1)眼のみ，(2)眼と口，(3)眼・口・鼻，(4)眼・口・鼻・眉と，徐々に顔らしく見える顔図形の組をつくり，場の複雑度のポテンシャル値に対する変化を調べた．
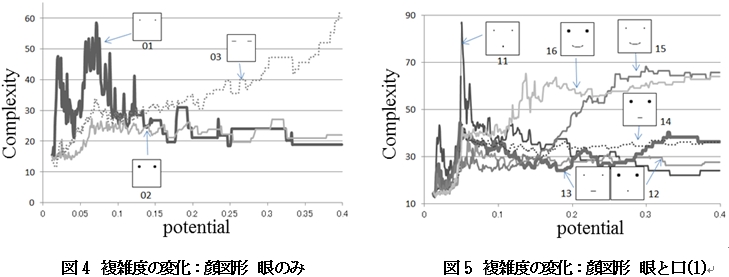
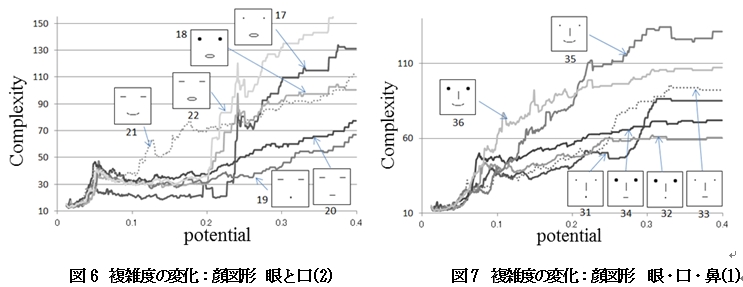
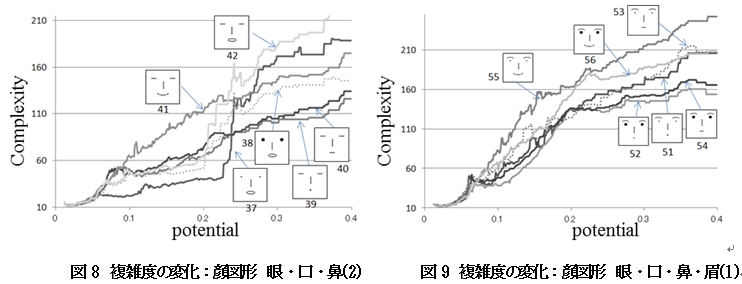
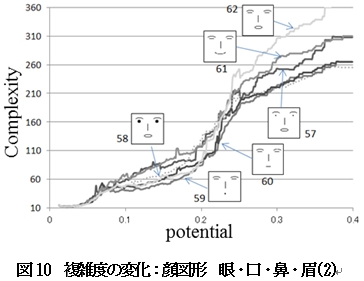
　図4は，眼のみで構成された顔図形について，縦軸に場の複雑度，横軸に場のポテンシャル値をとったグラフで，グラフ中の図形は顔図形を示す．同様に，図5と図6は眼と口，図7と図8は眼・口・鼻，図9と図10は眼・口・鼻・眉で構成された顔図形についてのグラフである．

　眼のみの顔図形の場合，単に離れた2点にしか見えないが，複雑度の変化にシグモイド関数の特徴である平坦部は見られない（図4）．眼に口を加えた顔図形の場合，複雑度は単調増加傾向があり（図5，7），図7の顔図形17，18などにシグモイド関数の特徴である平坦部のような部分が見られる．以降，図7，8，9と，顔の部品が増えるごとに，複雑度の変化がよりシグモイド関数らしい，平坦部と立ち上がりの部分がはっきりしてくる．線画だがほぼ顔として見える顔図形である図10は，ほぼシグモイド関数と見られる変化になっている．

　複雑度の変化がシグモイド関数らしいかどうか調べるため，顔図形の複雑度の変化をシグモイド関数で近似して，シグモイド関数のパラメータを比較する．
　視知覚の場の分布の複雑度をC，ポテンシャル値を x，a, b, t, p を定数とするとシグモイド関数は次式で表される．

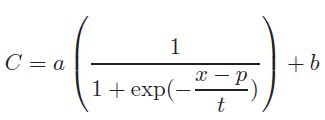
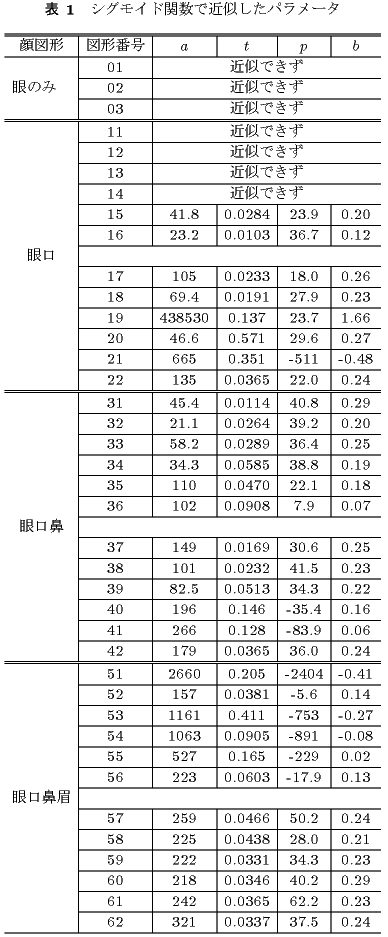
　表1に，図4から図10を上式で近似したパラメータを示す．表の図形番号は，グラフ内の顔図形の番号である．表1から，眼のみの顔図形01から03は，シグモイド関数で近似できず，シグモイド関数にはならない．
　眼に口を加えた顔図形11から14は，顔だと言われれば，顔に見えないことがないが，単に3つ点が離れた図形に見え，シグモイド関数で近似できず，シグモイド関数にはならない．
　眼に口を加えた顔図形15，16は，シグモイド関数で近似可能で，顔らしく見える．顔図形17から62は，全てシグモイド関数で近似でき，明確に顔と認識できる．このことから，シグモイド関数で近似できるかどうかで，顔らしく見えるか判断できると考えられる．
　本研究と同じ64×64ドットの大きさの顔画像の視知覚の場を検討した例（長石，2014）では，シグモイド関数で近似したパラメータは，aが300-400程度，tが0.03-0.1程度である．この範囲のものは，構成要素が多い顔図形37から62である．
　また，顔図形19，21，40，41，51，53，54は，顔らしくは見えるが，口が小さいためバランスが悪く，やや顔らしさが欠けているように見える．これらの顔図形のグラフをシグモイド関数で近似したパラメータは，他の顔図形のパラメータからはずれている（例：aが1000以上）．

●　むすび

　図形が形やまとまりとして見える場合，図形の視知覚の場の複雑度の変化が，ポテンシャル値のシグモイド関数になっているか，顔図形で検討した．
　その結果，顔らしく見える図形は，シグモイド関数になっていることが示された．また，部品の互いの間隔，長さの相対関係で，顔らしさが失われると，シグモイド関数による近似性が劣る．
　以上から，場の複雑度の変化がシグモイド関数になっているか，シグモイド関数をどの位満たしているかが，図形の形らしさを決める尺度になり得ると考えられる．そして，視知覚の場の複雑度の変化の仕方が，図形が形やまとまりとして見える上での1つの要素と考えられる．

参考文献

　遠藤信貴・齋木潤・中尾陽子・齋藤洋典(2003) . 無意味輪郭図形の階層的特徴記述に基づく知覚判断性分析 . 『心理学研究』, 74 (4)，346-353 .

　行場次朗 (1995) . 認知心理学重要研究集１―視覚. 『誠信書房』

　長谷川純一・輿水大和・中山晶・横井茂樹 (1986). 『画像処理の基本技法 ―技法入門編 ―』. 技術評論社 .

　長石道博 (1996). 視覚の誘導場モデルを用いたパターン認識時心理実験結果検証 . 『テレビジョン学会論文誌』, 50 (12), 1965-1973.

　長石道博 (1998). 視覚の誘導場による読み易い和文字列表示 . 『映像情報メディア学会誌』 , 52 (12), 1865-1872.

　長石道博 (2003). 視覚の誘導場による感性評価 .『認知科学』, 10 (2), 326-333.

　長石道博 (2005). 視覚の誘導場モデルによる画素密度と文字読み易さ関す心理実験結果検証 .『認知科学』 , 12 (3), 287-295.

　長石道博 (2014). 視知覚の場による顔表情認モデル検討. 『映像情報メディア学会誌』, 68 (9), J414-416 .

　S.J.Lupker(1979) ``On the nature of perceptual information during letter perception''， Perception & Psychophysics, 5(4), pp.303-312

　内山道明 (1967) ．視覚場の時間的変容過程に関する研究．『名古屋大学文部研究論集 (哲学)』, 45-85

　内山道明 (1968) ．視覚場の時間的変容過程に関する研究 (その 2) ．『名古屋大学文部研究論集 (哲学)』. 81-91

　横瀬善正 (1986).『形の心理学』. 名古屋大学出版会

本ページの原典
　長石道博，視知覚の場による形らしさ検討　日本認知科学会　テクニカルレポート JCSS-TR-73 1-9 (2015)