● 重力レンズ錯視
「小さな点は近くの大きな図形に引き寄せられるように見える」という錯視現象である。
図1のように,例えば,平行四辺形を成す小さな4点の周辺にやや大きな円を置くと,やや大きな円に引き寄せられ,小さな点が平行四辺形を成しているようには見えない。図2は,小さな4点のみにした場合である。
図1と見比べると,やや大きな円の影響で,小さい点の配置が平行四辺形に見えなくなっている。
この現象は,重力場のモデルで説明できるので「重力レンズ錯視」と呼ばれている1)。
詳しい重力レンズ錯視の解説,デモ
http://www.brl.ntt.co.jp/IllusionForum/v/gravityLens/ja/index.html
|
 
図1 重力レンズ錯視の例 図2 小さい点のみ
|
|
● 視覚の誘導場による重力レンズ錯視現象の解釈可能性
誘導場のあるポテンシャル値の分布を調べることで,Müller-Lyer の錯視図形の長さの説明2), 3)や
ポッゲンドルフ錯視4), 5),点列の錯視量6)など,実体のある図形の錯視量の定量的説明ができることが示されている.
また,主観的輪郭のような実際にパターンが存在しないような例は直接的な説明はできていない7).た
だし,主観的輪郭を引き起こすパターンの位置や背景などを変えると錯視の見え方がかなり異なる.こう
した動的な主観的輪郭の見え方の違いを誘導場の分布を利用して説明できる可能性が示唆されている8).
以上の研究から,何か錯視を起こすパターンが存在し,その影響が何らかの空間的に波及する現象であれば,
誘導場で説明できると考えられる。
したがって,誘導場は重力レンズ錯視現象の解釈できる可能性が高いと考えられる。
|
● 重力レンズ錯視の図形がつくる誘導場
まず,重力レンズ錯視を引き起こす図形の周りに生じる誘導場を計算,観察した。
http://www.brl.ntt.co.jp/IllusionForum/v/gravityLens/ja/index.html のページの重力レンズ錯視の図形を元に,白黒2値化して,192×192dot(72dpi)の画像に変換後,誘導場を計算した。
図3は,図1のような,平行四辺形を構成する小点の脇に大きな円を配し,
重力レンズ錯視が生ずる場合について,誘導場を計算,誘導場の分布を等ポテンシャル線で表示した例である。
図4は,図1の小点のみの図形について誘導場を計算した例である。
小点のみの場合,図4のように,誘導場の分布が平行四辺形の形に層状に分布している。
ところが,小点の脇に大きな円があると,図3のように,誘導場の分布が元の
平行四辺形ではなく,大きな円のある方向にずれたような分布になっている。
この,図4の平行四辺形的な誘導場の分布と,
大きな円の影響による,図3の非平行四辺形的な分布の違いを人間が認知し,
本来平行四辺形である誘導場の分布が,平行四辺形の分布でないために,錯視として認識されるのではないかと考えられる。
|
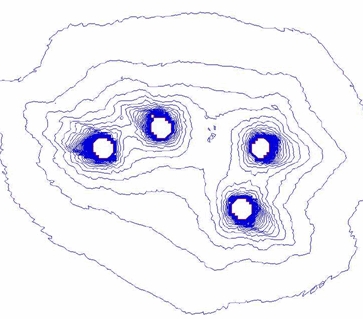
図3 重力レンズ錯視の図形がつくる誘導場の例
|
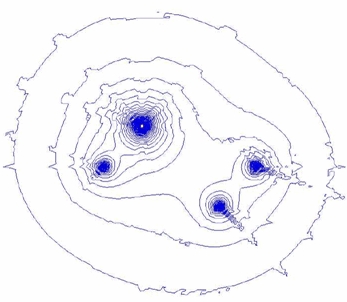
図4 平行四辺形を構成する小点がつくる誘導場の例
|
|
● 重力レンズ錯視の解析
大きな円が,本来平行四辺形に布置された小点を非平行四辺形的な分布と見える影響を及ぼしていることを
明らかにするため,大きな円,または小点がある場合とない場合で誘導場の違いを分析した。
重力レンズ錯視を構成する,大きな円+小点,小点のみ,大きな円のみ の3つ図形について,
誘導場を計算,比較し,小点や大きな円の影響を調べる。
図5は,図1から小点を除いて,大きな円のみの図形,図6は,図5の
誘導場の例である。
|

図5 大きな円のみ(図1から小点を除いた場合)
|
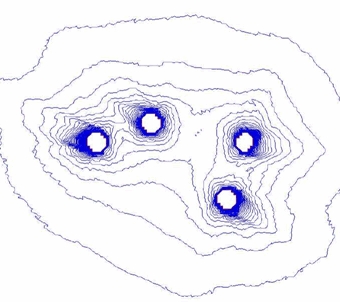
図6 大きな円のみ図形がつくる誘導場の例
|
A: 誘導場の強さ: (大きな円+小点)−(大きな円のみ) の場合
図7は,図3の2次元上の誘導場の強さから,図6の誘導場の強さを差し引いた差分を
示した図である。図7の色は場の強さで,黒 → 青 → 赤 の順に強いことを示す。
大きな円の小点が存在する円弧上を中心に,大きな円の接線方向に強い場(赤や青)が生じていることがわかる。
図8(a)は,図7の特に場の強い赤や青の部分を白黒表示にし,元の小点,大きな円の図形を入れた図である。
大きな円の接線方向に生ずる,場の強い部分が,図8(b)のように,平行四辺形が崩れる方向と一致するように見える。
このことから,大きな円の接線方向に生ずる場の強い部分が,重力レンズ錯視現象を引き起こしていると考えられる。
|

図7 誘導場:(大きな円+小点)−(大きな円のみ)の差分
|
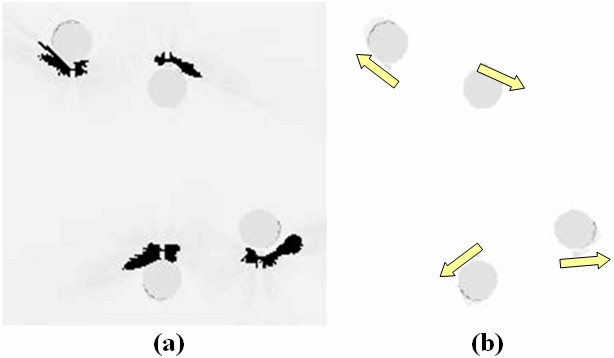
図8 図7の差分が大きい部分
|
B: 誘導場の強さ: (大きな円+小点)−(小点のみ) の場合
図9は,図3の2次元上の誘導場の強さから,図4の誘導場の強さを差し引いた差分を
示した図である。大きな円の付近の誘導場は,円の周囲に均一に分布するのではなく,小点の反対側に回り込むように,彗星のような尾を引いたような分布になっている。この尾は小点の影響で生じていると考えられる。
図10(a)は,図9の特に場の強い赤や青の部分を白黒表示にし,元の小点,大きな円の図形を入れた図である。この尾と大きな円の中心を結ぶ方向が,図10(b)のように,平行四辺形が崩れる方向と一致するように見える。
このことから,Aの場合と同様,大きな円,小点の配置で作り出される,強い誘導場の部分が,重力レンズ錯視と関連していると考えられる。
|
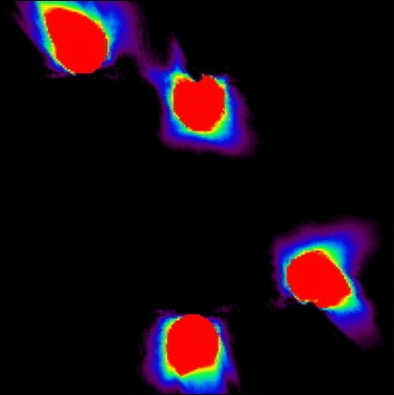
図9 誘導場:(大きな円+小点)−(小点のみ)の差分
|
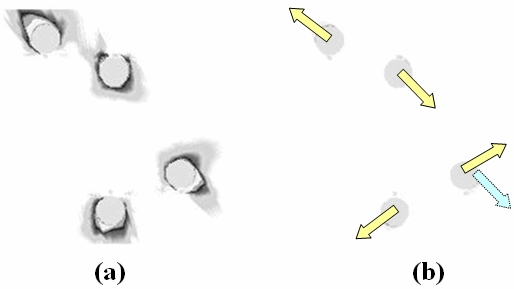
図10 図9の差分が大きい部分
|
【 考察 】
(場の強さの勾配)
大きな円,小点の配置で作り出される,強い誘導場の部分が,平行四辺形が崩れる方向と一致するように分布することから,この強い場の部分が重力レンズ錯視に関わっていることがわかった。
そして,この強い誘導場の部分は,大きな円の接線方向や尾のような誘導場の分布と大きな円の中心を結ぶ方向というように,方向性に特徴がある。
この方向は,図7,図9の場の強い「赤」の部分から,強さが弱くなっている「青」に向かっていることが観察される。
したがって,場の強さの勾配が大きい部分と平行四辺形の崩れる方向が一致している可能性が考えられる。
横瀬は,図8(b),図10(b)の矢印のような力を「ベクトル場」と呼び,いろいろな錯視図形の見え方を説明を試みている11)。ベクトル場は,図形がある点につくる誘導場の強さを,ある点以外の図形に及ぼす「分力」と解釈されている。このことから,誘導場で重力レンズ錯視を考える場合,小点が大きな円に引き寄せられるような「力」のようなものが働いており,その「力」は誘導場の勾配から推察できると考えられる。
しかし,「ベクトル場」の力点,作用点など,「力」の作用に対する概念規定が不十分で,視覚の誘導場の強さとの関連性が明確でないという問題がある11)。
今回,「力」というものを表現するのに,誘導場の勾配が有効という示唆を得た。
電磁気学でも,場で生ずる「力」(作用)は,場の強さの勾配で解釈される。
横瀬の「ベクトル場」の場の分力のような解釈ではなく,誘導場の勾配のほうが自然であると考えられる。
したがって,錯視理解には,誘導場の勾配が妥当と考えられる。
なお,図10(b)の水色破線の矢印のように,誘導場の強さの勾配が大きそうな部分が,必ずしも平行四辺形の崩れる方向ではない場合も見られる。これは,単純に誘導場の勾配の大小だけでなく,周囲との関連性など,他の要素も考慮する必要性を示唆していると考えられる。
今後,錯視の影響がある勾配を求める位置,場の強さの範囲などを考慮し,錯視量,錯視の生ずる方向の定量化を検討したい。
(場の勾配と視覚現象)
このような,誘導場の強さの勾配が,視覚現象と関わっている可能性が,
視覚の誘導場の生理学的根拠として最も引き合いに出される,本川の網膜誘導の場11)において報告されている12)。
光点の像を網膜上で移動させると,移動による網膜誘導(網膜痕跡)が生ずる。誘導の値は運動の開始部で低く,終点で高くなる勾配ができ,勾配は光点の速度が大きいほど急である。
更に,大きな光点は勾配が緩やか,小さな光点は勾配が急である。
これらの結果から,同じ物理的速度なら小さい物体のほうが速く動いているように感じる心理学の法則が説明できるとされている12)。
また,A,B2点間を同時に照らす刺激を網膜に与えると,AとBの間に誘導の勾配が生じる。
しかし,AとBを適当な時間間隔で呈示し,仮現運動が生じると誘導の勾配が無くなり,A,Bどちらの方向の運動か区別できない。
このように,本川の実験より,誘導の勾配が運動視と関連することが示されている。
そして,本研究の重力レンズ錯視でも,誘導場の強さの勾配が錯視方向と関連していることが示唆された。
したがって,誘導場の強さの勾配,ないしは,異なる強さの誘導場の分布の違いが,視覚現象の説明に有意義であると考えられる。
(誘導場の差分による錯視現象の説明)
これまでの誘導場による錯視現象の説明では,錯視が生ずる図形の周りの誘導場の分布状態を論じていた2), 3), 4), 5), 6)。
しかし,主観的輪郭のように,なかなか良い説明ができない錯視現象もある7)。
今回の重力レンズ錯視の解析では,生ずる図形の構成要素別に誘導場を求め,差分から錯視に影響を与えている状況を分析することで,何が錯視に関連しているのか,どうすれば定量化できるかのヒントが得られた。
今後,他の錯視現象について,錯視図形の構成要素別に誘導場の差分を,錯視現象の説明や,定量化に応用する可能性を検討したい。
また,誘導場による視覚現象の説明において,差分による分析を,前述の場の勾配と共に,従来の誘導場の分布の計量中心の分析以外の手段として着目,検討して行きたい。
(誘導場で重力レンズ錯視が説明できる理由)
重力レンズ錯視は,古典的電磁場のような,等方一様な「場」では説明できないため,重力場のモデルを導入し,錯視現象の定量説明が可能になっている錯視である1)。
一方,視覚の誘導場は,物理的には古典的電磁場に近いものであるが,なぜ,定性的ではあるが,重力レンズ錯視が説明できることを示す結果が得られたのだろうか。
視覚の誘導場は,基本は古典的電磁場であるが,遮蔽(奥に隠れて見えない部分は場の形成に寄与しない)という性質がある。
これは,古典的電磁場にはない性質である。この性質のおかげで,文字の切り出し9)や感性評価10)が可能になっている。
同様にこのような遮蔽の性質が,視覚の誘導場に非等方的な状態を与え,その結果,重力レンズ錯視にも対応できたと考えられる。
|
参考文献
1) Naito, S., (1994) The Gravity Lens Illusion and its Mathematical Model. In G. H. Fischer & D.Laming (Eds.) Contributions to Mathematical Psychology, Psychometrics, and Methodology Recent Research in Psychology, Springer-Verlag New York, Inc.
2)長石道博. 錯視図形がつくる視覚の誘導場の解析. TV学会年次大会, Vol. 7-14, 1993.
3)白石照美, 深水義之, 吉田登美男, 伊藤明. ミューラー・リヤー錯視図形の視空間伝達特性モデル F (1) による解析 : 景観の図形認識の立場からの解明と評価に関する研究(7) . デザイン学研究 Vol.47, No.1, pp.35-42, 2000
4)中島和樹, 菅沼義昇, 伊藤正美. 心理的ポテンシャル場とニュ−ラルネットによる図形認識. 電子情報
通信学会技報, PRU90-155, pp.79-86, 1990.
5)細木寛志, 黒田巧, 東恒人, 入江浩一. 図形の誘導場の簡易計算法. 電子情報通信学会総合大会, Vol.A-385, p.386, 1996.
6)東恒人, 島田恭宏, 前田征大.点列の周りに生じた誘導場を用いた錯視量の推定法,映像情報メディア学会誌 Vol.59, No.9, pp.1325-1332, 2005
7)野澤晨. 空間と時間, 第5章. 彰国社, 1975.
8)高木敬雄, 小村緩岳. 主観的輪郭線の効果. ラウンドテーブル No.28, 日本心理学会 第62回大会, pp.2-10, 1998.
9)長石道博: "視覚の誘導場を用いた手書き文字の切出し", 電子情報通信学会論文誌, J 76-D-II, 9, pp.1948-1956 (1993 9)
10)長石道博,視覚の誘導場による感性評価,『認知科学』,Vol.10,No.2, pp.326-333 (2003)
11)大山正, 今井省吾, 和気典二編 「感覚・知覚心理学ハンドブック」 誠信書房 (1969)
*最新版(1994)に誘導場の記載はありません
12)本川弘一,視覚の心理・生理,テレビジョン学会誌,Vol.16, No.7, pp.425-431 1962.7
本ページの原典
長石道博: "視覚の誘導場による重力レンズ錯視の解釈",日本認知科学会 テクニカルレポート JCSS-TR-64 (2009.7.10)
|
Copyright 2019 [Michihiro Nagaishi]. All rights reserved.