横瀬が誘導場の計算式を考えようとした目的に,誘導場の応用があった1)。
その応用として,誘導場による文字認識が考えられていた。
しかし,誘導場をどのようにすれば,パターン認識が可能かは明らかにできなかった。
このページでは,まず,一般的なパターン認識方法の考え方,認知モデルなどを説明する。
続いて,ダイナミクスと場による認知モデルの考え方を述べ,誘導場によるパターン認識モデルを解説する。
|
● 従来の文字パターン認知の研究
認知心理学では,人間の情報処理機構をBlack Box とみなし,適当な入力(刺激)を与えた時の出力を観
測することでBlack Box の機構を推測する2).いろいろな入出力の形態や段階などがあるが,Black Box
を中心としたこの関係は 図1 のBrunswik の図式 としてまとめられている3), 4).図1 の7本の縦線c,b,a,O,A,B,C はBlack Box をめぐって生じる事象の因果の前後関係を示している.この方法論は,物理学
者が伝統的に行う,物をぶつけて物質の状態を推測する方法注1に似ている5).これまで,この方法によって人間の情報処理機構,とりわけ文字パターン認識など視覚は非常に良く調べられ,認知機構のモデルがつくられてきた2),6), 7), 8) 9) .もちろん,Black Box の実体は生理学的に決定されるべきものである2),10) .
しかし,認知心理学の方法は,人間の情報処理機構の基本的枠組みなどの重要な概念を提供してくれる上で大変重要である2),6),10) .この枠組みやアナロジは工学的に応用する際の有効な指針として利用できると考えられる11).
|
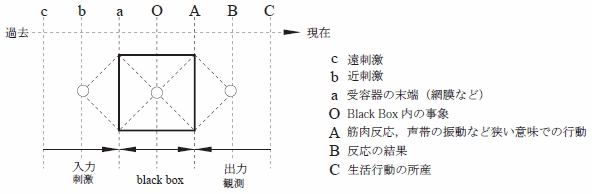
図1 現代心理学の考え方:Brunswik の図式 3)
|
最初に文字パターン認知のモデルとして明確化されたモデルに,セルフリッジ(Selfridge)のパンデモ
ニアム・モデル(Pandemonium model)がある12), 7).このモデルでは,デーモン(daemon)と呼ばれる
個々のモジュールが協力することで,文字パターンなどのイメージから特徴を抽出し,更に様々な情報を統
合して認識が行われる概念を示した.今日の工学的文字認識の過程はこのモデルの構造に非常に近い12), 7).
パンデモニアム・モデルは極めて抽象的なモデルである.そこで,図2 の例のような文字パターンの
認知モデル13) を仮定し,実際に人間が判断する文字パターンなどの類似性の心理実験結果と認知モデルの
評価値を比較して,モデルの有効性を検討する数理モデルの研究が行われている11), 12), 9).数理モデルは
Brunswik の図式のBlack Box を具体化したものである.そして,同じ文字パターンを数理モデルと人間に
入力し,双方の出力を比べることで仮定したモデルの内容を検討する.
数理モデルはTownsend らによって初めて明確化された12).その後,様々なパターンの数理モデルが検
討された19), 30).しかし,そのほとんどが線分のみで構成された人工的な線図形などのパターンを対象とし
ており,我々が日常使う活字や手書き文字の数理モデルは検討されていない9).また,数理モデルごとに
類似性を説明できるパターンが限られており11),様々なパターンの類似性を統一的に説明できる数理モデ
ルはほとんど検討されていない11), 9).
注1: 例えば,ラザフォードは薄い金の板にぶつけた電子の反射から原子核を発見した.
|

図2 文字パターンの認知のモデル 13)
|
● ダイナミクスと場によるモデル
このように,いろいろな文字パターン認知に関する数理モデルの検討や人間の類似性判断などの心理実
験が行われている.しかし,これまで提案された数理モデルで説明できるパターン種は限られており,いろ
いろなパターンの類似性を統一的に説明する数理モデルはまだ提案されていない.
今井は,これまで提案された文字パターン一般に有効な特徴の決定やパターンの特徴を用いる数理モデ
ルの構築が困難なのは,パターン認知過程が,例えば,前述のパンデモニアム・モデルのような,パ
ターンから「特徴」を抽出,分析する過程ではなく,一方のパターンが他方のパターンに一致するような変
換をパターンに施す過程,すなわち,ダイナミクスであることによるとしている.今井は,具体的なダイナ
ミクスとして変換構造説を提案している14).従来の視知覚研究に関する知見4),15),年齢別変形文字の読まれ方の研究1),パターン変換作用による視覚恒常性の説明16) などが,今井と同様に,パターン認知はダイナミクスであることを示唆している.
また,電磁気力を想定した力学的モデルによる手書き文字の識別17),発振ニューラルネットモデルによ
る手書き文字変形の再現18) などが,手書きなど複雑な文字パターンの認知機構にダイナミクスが存在す
る可能性を示唆している.これらの研究から,ダイナミクスによるパターン認知モデルはいろいろな文字
パターンを実際に説明できる可能性が高いと考えられる.
最近,文字パターンの認知などの視知覚を統一的に説明する枠組として,
「場」が注目されている.その「場」として,図形の周囲に波及する「場」を考える
ことにより,視覚現象を説明する横瀬の視覚の誘導場があり,パターンの類似性が評価などの可能性が示唆
されている.したがって,ダイナミクスによる誘導場のパターン認識が数理モデル化できれば,このモデルによってこれまで研究されてきたパターン認知の心理実験結果を統一的に説明できる可能性が高いと考え
られる.
|
● 誘導場によるパターン認識モデル
視覚の誘導場理論で明らかにされているのは,「パターンが,どのように見えるか」だけであり,パタ−
ン認識がどのように行われるのかに関してはほとんどわかっていない3), 4).しかし,横瀬は誘導場の等ポ
テンシャル線の分布の類似性が,パターンを見分ける上で重要なことを示している1) ことから,等ポテン
シャル線の分布の違いが評価できれば,誘導場を使ってパターンを認識できる可能性がある.
等ポテンシャル線の分布の評価法として,まず,場を重ね合わせて類似度を求める鋳型照合12) が考えら
れる.しかし横瀬は,片仮名やあるアルファベットの線分の一部を分離するなどして,別のアルファベット
に変化させた変形パターンの読まれ方の研究から,等ポテンシャル線の分布の部分的な類似性の違いだけ
ではなく,全体的な分布の違いも評価できなければならないこと,そしてこれは,パターン類似性がゲシタ
ルト心理学のパターンの良さと関連があり,パターンの良さは誘導場の分布で説明できることを示唆してい
る1).ところが,鋳型照合は「場」の強度を座標点に依存する独立変数と考えるため,基本的に分布の微
視的な違いしか評価できず,横瀬の示唆する全体の違いやパターンの良さを評価するには問題がある.
一方,横瀬はせん断変形を受けたパターンの読まれ方の研究から,誘導場が一致するようにトポロジカル
な変形を行い,同相ならばそのパターンは類似である可能性を示唆している1).これは,「場」におけるダ
イナミクスによる認識モデルの存在を示唆するものと考えられる.実際,パターン認識などの視知覚を説明
する枠組として,ダイナミクスの重要性が指摘されており,前述のように,「場」はダイナミクスの力学的概念として捉え
られている.特に今井は,ゲシタルト心理学のプレグナンツの原理におけるパターンの
良さを定量化するという観点から,具体的な認識モデルとして道筋モデルを提案し,パターンの類似性が
パターンの良さと関連することを示している14).道筋モデルは,パターン相互の変換可能性の程度によっ
てパターンの類似性を評価するモデルで,パターンの特徴を使わずに1次元点列パターンの類似性を定量
的に説明できることが検証されている19).したがって,今井の道筋モデルを誘導場に応用すれば,横瀬が
示唆した誘導場の等ポテンシャル線の分布の類似性を評価できる認識モデルを実現できる可能性が高いと
考えられる.
道筋モデルは,パターンA に変換を行ってパターンB に一致するまでの変換の手続き(道筋の長さ)を
パターンA,B 間の類似性の尺度とする.すなわち,パターンA とパターンB の一致に多くの変換が必要
ならば,パターンA,B 間の類似性は低く,変換が容易ならば類似性が高い34).変換を等ポテンシャル線
の分布の変位,道筋を分布を一致させるのに必要な変位量とおけば,誘導場の変形による次のパターン認
識モデルが考えられる.まず,図3(a) の未知パターンA の誘導場と,複数のパターンB, C, D... の誘導
場を準備し,A を変形して他の誘導場と一致するのに必要な変位を求める.図3(b) のA とB, C, D... 間の線分の長さは変位量を示す.例えば,A とC は分布が非常に似ており,少ない変換で一致させられるた
め,A とB よりも変位量が少ない.したがって,A との間の変位量が一番小さい誘導場のパターンが認識
結果となる。
|
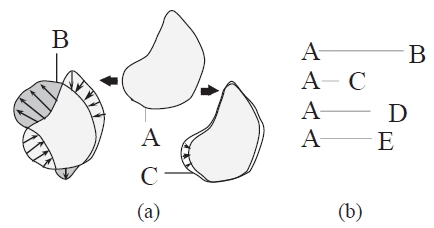
図3 誘導場によるパターン認識モデルの概念
|
● 認識アルゴリズム
視覚の誘導場は,基本的にクーロンポテンシャルと解釈できるので,誘導場の変化を薄膜のような弾性
体のアナロジで考えることができる.ある誘導場の等ポテンシャル線の分布を他方の分布に一致するよう
に変位させると,弾性体と見なした誘導場に歪みが生ずる.歪みは弾性エネルギで一意に表現できるので,
誘導場の変換量を弾性エネルギを用いて評価する20).
図4 のように,辞書パターン i 「士」と未知パターン j 「土」の誘導場の重心を一致させ,ポテンシャル
値 p の等ポテンシャル面毎に「土」の誘導場の等ポテンシャル線の輪郭線上のすべての点が,その点の法
線方向(輪郭線上の矢印)上にある「士」の等ポテンシャル線の輪郭線に変位したと仮定し,等ポテンシャ
ル面ごとに生ずる弾性エネルギ ei(p) を計算する.弾性エネルギ ei(p) は,輪郭線に張られた膜が平衡状態からある位置まで変位するエネルギである,膜の変形に要するエネルギ U1 と,膜の縁である輪郭線の変形に要するエネルギ U2 の和である21).U1 は変位を u(x, y),膜の張力 τ,α = τ/2 とすれば,
|

|
|
となる.U2 は,膜の張力 τ,密度ρ ,弾性係数は一様で C,β = (τ2/ρ2) C とすると次式で与えられる.
|

|
|
未知パターン j が辞書 i の誘導場との一致に要する総弾性エネルギ Eij が最小な辞書 i が認識結果となる。
なお,弾性エネルギの詳しい計算方法などは,このページ末の付録を参照。
|

|

図4 認識過程
|
● 誘導場による文字パターン認識モデルの検証
この誘導場のパターン認識モデルが,いろいろなパターン認知の心理実験結果を,統一的に説明できることを
検証した。検証には,複数の心理実験結果と,実験で使われたパタ−ンの違いについて,誘導場モデルの弾性エ
ネルギで評価した結果を比較した.検証した文字パターンは,人工的な線図形,活字,変形パターン,そして手書き文字である。詳しい検証結果は,文献 22), 23), 24), 25)を参照。
ここでは,検証方法,検証で使った文字パターン例,検証結果を説明する。
【検証方法】
いろいろなパターン認知の心理実験で使われた文字パターンの違いを誘導場モデルの弾性エネルギで評価する。
文字パターンを64 × 64 dot の大きさに作成し,パターンの領域を含む128 × 128 dot の範囲で誘導場を計算する。
そして,図4のパタ−ン i, j の誘導場について,等ポテンシャル線がデータの枠に接触しないポテンシャル値 0.03 から文字線分付近の0.39 まで0.01 ずつの各等ポ
テンシャル面で弾性エネルギ ei(p) を求め,その総和 Eij を,パタ−ンi, j 間の,誘導場の弾性エネルギとする.なお,ほぼ同じパターン間のエネルギを計算した場合,U1 と U2 がほぼ等しい値になるよう,α=β/2 = 1.0 とおいた.
誘導場の弾性エネルギの比較対象に,まず「場」の概念を利用した文字認識で最もよく使われる,「場」の強さをEuclid 距離で評価する方法26) を適用し,誘導場のEuclid 距離とした。
続いて,同じく比較用として優れた手書き文字認識性能が報告されており,文字認識の研究のリファレ
ンスとして最もよく使われるLDCD 特徴(Local Direction Contributivity Density Feature)27) をEuclid
距離で評価する方法を適用した.LDCD 特徴は,64 × 64 dot の文字パタ−ンを,8 × 8 メッシュに分割,n 番目(1 ≦ n ≦ 64)のメッシュについて,水平,垂直,+45 度,-45 度 の4 方向の方向寄与度(Direction Contributivity Density)27) を求め,最終的に256 次元の LDCD 特徴の Euclid 距離とした。
Euclid 距離はパターンの類似性が高いほどゼロに近づく.
以上のように求めた誘導場の弾性エネルギ,誘導場のEuclid 距離,LDCD 特徴のEuclid 距離の3つの評価方法と心理実験結果との相関を求める.対象パターン,心理実験結果,3つの評価方法の関係を図5 にまとめた.図5 のように,検証に用いたパターンに対し,心理実験による人間が評価した類似性が視覚の誘導場の弾性エネルギで説明できるか比較する.その際,誘導場の Euclid 距離と LDCD 特徴のEuclid 距離を比較基準として用いる.
|

図5 3つの評価方法による検証
|
【検証で使った文字パターン例】
図6 線図形(直線で構成された図形,漢字): 文献 22) で検証
図7 活字: 文献 23) で検証
図8 変形パターン(線分の一部を変更): 文献 24) で検証
図9 手書き文字: 文献 25) で検証
|

図6 文字パターン例:線図形
|

図7 文字パターン例:活字
|

図8 文字パターン例:変形パターン 横瀬の例1)
|

図9 文字パターン例:手書き文字 評定した100文字種
|
【検証結果】
各検証パターンの心理実験結果との相関係数と検定結果を検証パターンごとに表にまとめた。表の数字は相関係数である。
◎○△は,誘導場の弾性エネルギが,他の2つの評価方法に対する有意差を t 検定した結果で,◎ は 1,5,10 %,○ は 5,10 %,△ は 10 % の危険率で,誘導場の弾性エネルギが有意である場合を示す。
表1 検証結果: 線図形(直線で構成された図形,漢字)
| パターン | 誘導場 弾性エネルギ | 誘導場 Euclid 距離 | LDCD 特徴 Euclid 距離 |
| 線図形 | 0.540 | 0.360 (○) | 0.380 (○) |
| 漢字 set1 | 0.692 | 0.420 (◎) | 0.351 (◎) |
| 漢字 set2 | 0.672 | 0.514 (△) | 0.463 (○) |
| 漢字 set3 | 0.763 | 0.703 (×) | 0.627 (○) |
表2 検証結果: 活字
| パターン | 誘導場 弾性エネルギ | 誘導場 Euclid 距離 | LDCD 特徴 Euclid 距離 |
| アルファベット大文字 | 0.531 | 0.461 (○) | 0.464 (○) |
| アルファベット小文字 | 0.584 | 0.484 (◎) | 0.513 (△) |
| カタカナ | 0.436 | 0.350 (○) | 0.366 (△) |
アルファベット大文字
(ドット) | 0.351 | 0.305 (○) | 0.311 (○) |
| ひらがな | 0.285 | 0.159 (◎) | 0.190 (◎) |
表3 検証結果: 変形パターン(線分の一部を変更)
| パターン | 誘導場 弾性エネルギ | 誘導場 Euclid 距離 | LDCD 特徴 Euclid 距離 |
| アルファベット | 0.900 | 0.652 (◎) | 0.772 (○) |
| アルファベット2 | 0.939 | 0.455 (◎) | 0.855 (△) |
| カタカナ | 0.922 | 0.596 (◎) | 0.693 (◎) |
横瀬1
(ドット) | 0.752 | 0.454 (○) | 0.455 (○) |
| 横瀬2 | 0.972 | 0.819 (△) | 0.772 (△) |
表4 検証結果: 手書き文字
| 漢字 | 誘導場 弾性エネルギ | 誘導場 Euclid 距離 | LDCD 特徴 Euclid 距離 |
| 小 | 0.793 | 0.551 | 0.515 |
| 口 | 0.406 | 0.226 | 0.386 |
| 心 | 0.741 | 0.530 | 0.579 |
| 火 | 0.802 | 0.586 | 0.579 |
| 牛 | 0.788 | 0.560 | 0.634 |
| 必 | 0.333 | 0.206 | 0.260 |
| 史 | 0.989 | 0.656 | 0.681 |
| 世 | 0.670 | 0.394 | 0.310 |
| 古 | 0.707 | 0.508 | 0.439 |
| 次 | 0.875 | 0.628 | 0.675 |
| 考 | 0.631 | 0.337 | 0.445 |
| 成 | 0.933 | 0.570 | 0.727 |
| 冷 | 0.879 | 0.652 | 0.805 |
| 我 | 0.634 | 0.312 | 0.276 |
| 100種 平均 | 0.599 | 0.486 (◎) | 0.497 (◎) |
表1〜4の例が示すように,人工的な線図形,活字,変形パターン,手書き文字について,誘導場による文字認識モデルの有効性について検証した.その結果,各対象パターン共に誘導場モデルの弾性エネルギが他の2つの評定方法よりも心理学実験結果をよく説明できることが示された.このことから,誘導場モデルは広範囲なパターンの類似性が説明できるモデルとして妥当と考えられる.
|
【文字認識】
誘導場モデルを手書き文字認識に用いた場合の認識能力を示す.誘導場の計算,弾性エネルギによる識別は,上記の検証方法と同じである.また,従来手法としてLDCD 特徴27)の類似度と比較した。なお,最適な辞書を決定するための学習は一切行っていない.
電子技術総合研究所の手書き数字データべ−スETL1 28) の数字(0 から9)から,任意に選んだ100 文字を,同じETL1 のデータベース第1番目の文字を辞書として認識を行った.また,同ETL9 29) の平仮名から任意に選んだ20 文字種を,「現代書道字典」(阿保直彦編著、木耳社)から,イメージスキャナ(400 DPI)で読み取った楷書体の手書きの平仮名を辞書として認識を行った.各認識結果の認識率(%)の一例と全手書き文字の平均認識率を表5 に示した。
誘導場とLDCD 特徴の認識率は文字種により異なるが,平均値などから従来手法と同程度の認識能力があることがわかる.
|
表5 手書き文字認識結果例

|
【考察】
誘導場の認識モデルは人間のパタ−ン認知過程を説明する数理モデルのひとつとして有効であることが示された。
では,なぜ,誘導場の認識モデルが文字パターンの類似性の評価に優れているのであろうか.
検証に用いた多くのパターンについて,誘導場の強さおよびLDCD 特徴でEuclid 距離を用いた評価方法は,心理
実験結果との相関が弾性エネルギより弱い.Euclid 距離を用いた場合,正解パターンおよび基準パターンの評価結果が回帰直線からはずれることが多く,パターンの類似性を正しく評価することが難しくなっている.これは,今井14)が指摘しているように,Euclid 距離などパターン認識の識別に使う距離と,人間が判断するパタ−ンの類似性は必ずしも一致しないことを示していると考えられる.
一方,誘導場に弾性エネルギを用いた評価方法は心理実験結果とよく合致する.
誘導場モデルは,パターン認識はダイナミクスであるという見解から構築されており,これまでの対象文字パターンの構造などに依存する特徴を元にした方法ではない.
そして,ダイナミクスという前提で考案された誘導場モデルが,いろいろな文字パターンについて心理実験との相関が高くなっている.誘導場の認識モデルの枠組みであるダイナミクスは,パターン認識に関して重要な役割をもっており,その
結果として,いろいろな文字パターンに対して優れたパターン類似性の評価能力が得られたと考えられる.
人間は文中に誤字があっても,文字の類似性と文脈を利用して正しく読めることが報告されている30).
そこで,認識が難しい手書き文字などに対し,識別に使うEuclid 距離などを確信度として認識結果を補正
する知識処理が通常行われている.しかし,一般に確信度の信頼性が充分ではないため,通常人間が文
脈と類似文字の関連性から正解を予測する際の手順や知識を,認識結果の補正に応用しても好結果が得ら
れにくい.
一方,誘導場の認識モデルが評価するパターン類似性は,心理実験結果に近いことが示された.
したがって,誘導場を用いれば,手書き文字のような変形を伴うパターンについて,人間が行っている文字の類似性と文脈を利用する方法が充分機能し,文脈と類似文字の関連性から正解がより正確に予測できるようになり,認識率が向上すると考えられる.
|
● 認識性能を向上させるための課題
【パターンの正規化】
以上述べた類似性の検証や文字認識では,文字認識で一般的な文字パターンの大きさを揃える正規化は行っていない。
通常の文字認識で使う正規化が誘導場で有効かわからないからである。
そこで,活字などのパターンについて,従来文字認識で一般的に行われている文字の大きさ・位置の正規化が,
誘導場の弾性エネルギを求める場合に有効かどうか調べた.
表6 は,元パターンを正規化して誘導場を求めた場合の弾性エ
ネルギについて,正解パターンを除いた相関係数の平均を,正規化しなかった場合と比べた結果で
ある.表6 から,単純に元パターンの正規化を行うと心理実験結果との相関が弱くなる(平均 - 0.030)
ことがわかる.
活字の大きさを表すのにポイント数が使われる。同じポイント数でも,ベースラインからの高さが異なる文字がある。
このような活字に文字認識で一般的な正規化を行うと,高さが揃う。
しかし,表6 から,誘導場にはこのような正規化は不向きである。
文字の大きさが異なっても,ポイント数が統一されている状態が誘導場の弾性エネルギを求めるのに適している可能性が高い
と考えられる。
また,このことから,ポイント数が同じであっても,物理的な文字の大きさが異なるのは,文字自体の大
きさではなく,各文字の醸し出す場の広がりが揃うように,人間が経験的に文字をデザインしている可能
性が示唆されている3).これらから,誘導場の正規化は元パターンではなく,誘導場の広がりを揃える方
法が適していると考えられる.例えば,各等ポテンシャル面の広がりを同じ面積をもつ円の直径で近似し,
同じポテンシャル値ならば円の直径ができるだけ等しくなるように元パターンの大きさを調整して,誘導
場の分布を揃えるなどの方法が考えられる.
表6 誘導場の弾性エネルギにおける正規化の効果(活字)
| 線図形 | アルファベット小文字 | アルファベット(ドット) | カタカナ | ひらがな |
| -0.004 | -0.009 | -0.017 | -0.005 | -0.035 |
【各等ポテンシャル面の利用】
横瀬は変形文字の誘導場の観察から,人間はポテンシャル値が異なる複数の誘導場の分布の違いを総合的
に比較して,変形パターンの類似性を判断していることを示唆している1).
例えば,「あ」の場合,一番外側のポテンシャル値0.04 の等ポテンシャル面だけでなく,内側の0.08 や0.06 など
他の等ポテンシャル面も同時に比較する必要性を示している.
一方,提案した誘導場の認識モデルは,図4 に示すように複数の等ポテンシャル面における誘導場の歪みの総和を評価している.
そこで,誘導場の認識モデルにおいて,弾性エネルギを計算するポテンシャル値の範囲の違いがパターンの類似性評価に影
響するかどうか調べた.
表7 は,検証に用いた実験パターンの変形系列について,データの枠に接触しないポテンシャ
ル値0.03 からポテンシャル値0.20 までの低いポテンシャル値の範囲,およびポテンシャル値0.21 から文
字線分付近の0.39 までの高いポテンシャル値の範囲の2つの場合に分けて,ポテンシャル値0.01 ずつの各
等ポテンシャル面で計算した弾性エネルギによる相関係数と,ポテンシャル値0.03 から0.39 全ての弾性
エネルギを計算した場合の相関係数を比較した例である.
表7 の例を含め,弾性エネルギを計算するポテンシャル値の範囲によって,相関係数が大幅に異なる場合がある.
表7の太字は相関係数が高い場合である。
表から,単純にポテンシャル値0.03 から0.39 全ての弾性エネルギを計算した場合より,
低い,または高いポテンシャル値の範囲の弾性エネルギのほうが,類似性が高い場合が多い。
したがって,各等ポテンシャル面ごとの評価の仕方を解明すれば,パターンの類似性評価性能の向上が期待できる.
表7 ポテンシャル値による相関係数の違い
| ポテンシャル値範囲 | 0.03〜0.39 | 0.03〜0.20 | All (0.21〜0.39) |
| 変形文字 V-y | 0.983 | 0.981 | 0.339 |
| 変形文字 ユ−エ | 0.899 | 0.868 | 0.892 |
| 変形文字 コ−ヲ | 0.928 | 0.900 | 0.878 |
| 変形文字 横瀬 E | 0.966 | 0.989 | 0.503 |
| 変形文字 横瀬 T | 0.834 | 0.807 | 0.681 |
【誘導場間の変位計算】
ダイナミクスによる認識モデルにおけるパターンの変形操作は,回転や並進などの複合と考えられている14).
しかし,提案した誘導場の認識モデルは,変形を法線方向に限定したため,複雑な誘導場の変形を充分記述することができず,
心理実験との違いが生じたと考えられる.実際,変位をベクトルとして表示,観察すると,
図10 (a) のA,B,Cの変位のように,局所的に不適切な変位が生じている場合があり,その部分の弾性エネルギが 図10 (b) の矢印のように突出するため,類似性評価を悪くしている.
人間は,網膜に映る図形が大きさ,回転などの変形を受けていても,それらを同じものと知覚することが
できる恒常性があり,実際,「場」と恒常性の機構との関連性が示唆されている16).そして,「場」はわず
かな差異は一様化し,ある程度以上の性質の違いは反発して別になるよう,場全体が自動的により単純で最
も安定した状態に遷移するのが基本と考えられている3).
したがって,誘導場の認識モデルでは,例えば,
文字の大きさ・回転などの変形を通常の文字認識の前処理のように個々に行うのではなく,すべての変形を
区別せずに一括して誘導場全体を自動的に変形させるのが妥当と考えられる.具体的には,エネルギ最小
化原理を用いて,変位で生ずる弾性エネルギができるだけ小さくなるよう誘導場全体を変形させる変形操
作,例えばSnakes31) のように,変位方向を図形の形状に対して適応的に決定するコンピュータビジョン
的な手法が有効と考えられる
|

図10 変位が極端にずれている場合
|
参考文献
1) 横瀬善正著「形の心理学」
名古屋大学出版(1986)
2) フランシス・クリック著, 中原英臣, 佐川峻訳. DNAに魂はあるか−驚異の仮説−. 講談社, 1995.
3) 野澤晨. 空間と時間, 第5章. 彰国社, 1975.
4) 柿崎祐一. 心理学的知覚論序説, 培風館, 1993.
5) Tony Hey and Patrick Walters. 目で楽しむ量子力学(大場一郎訳), 第4 章. 丸善, 1989.
6) マイケルI. ポズナー, マーカスE. レイクル著, 養老孟司, 加藤雅子, 笠井清登訳. 脳を観る 一認知心
理学が明かす心の謎一, 第2 章. 日経サイエンス社, 1997.
7) D.E. ルーメルハート著, 御領謙訳. 人間の情報処理, 第2 章. サイエンス社, 1989.
8) 行場次朗編. 認知心理学重要研究集1―視覚認知, pp.64-105. 誠信書房, 1995.
9) 大山正, 今井省吾, 和気典二編. 新編 感覚・知覚心理学ハンドブック. 誠信書房, 1994.
10) 臼井支朗編. 脳・神経システムの数理モデル. 共立出版, 1997.
11) 横澤一彦, 淀川英司. 文字・図形の認知. テレビ誌, Vol. 40, No. 4, pp.244-250, 1986.
12) 行場次朗編. 認知心理学重要研究集1―視覚認知, pp.18-21. 誠信書房, 1995.
13) 横澤一彦, 梅田三千雄, 淀川英司. 人間の漢字パターン認識特性 ―線図形知覚特性に基づく認識モデルの提案とその有効性の検討―. 電子情報通信学会論文誌, Vol. J69-A, No. 5, pp.600-611, 1986.
14) 今井四郎. パターン認知の変換構造説(心理学モノグラフ17). 東京大学出版会, 1986.
15) 小川英光編. パターン認識・理解の新たな展開, 第2.6.4 章. 電子情報通信学会, 1993.
16) 小山隆正, 山崎敏正, 山ノ井高洋. 流れの場のパターン弁別モデル. 電子情報通信学会技報, Vol.PRU88-64, pp.33-39, 1988.
17) 久保田正, 藤村貞夫, 中路幸謙. 場による図形変形を用いた手書き文字の識別. 電子情報通信学会論文誌, Vol. J55-D, No. 5, pp.299-306, 1972.
18) 林幸雄. 人工ニュ−ラルネットワークによる時空間パターン処理に関する研究. ATR Technical Report,
Vol. TR-H-064, 1994.
19) 市川伸一, 行場次朗. パターンの精神物理学における方法論的諸問題の検討. 心理学評論, Vol. 27, pp.132-157, 1984.
20)長石道博,視覚の誘導場理論を用いた文字認識の提案 電子情報通信学会技報, Vol. PRU92-46, No.4,pp.7-14, 1992.
21) 恒藤敏彦. 弾性体と流体, 第2章. 岩波書店, 1995.
22) 長石道博:"視覚の誘導場モデルを用いたパターン認識時の心理実験結果の検証", テレビジョン学会誌誌, vol. 50,No.12, pp.1965-1973 (1996)
23) 長石道博:"視覚の誘導場モデルによる文字パターンの類似性に関する心理実験結果の検証", 映像情報メディア学会誌,Vol. 52,No.4, pp.594-601 (1998)
24) 長石道博:"視覚の誘導場モデルによる変形パターンの類似性に関する心理実験結果の検証",映像情報メディア学会誌,Vol. 53,No.3, pp.458-465 (1999)
25) 長石道博:"視覚の誘導場モデルによる手書き文字の文字品質評価と心理実験結果との比較",映像情報メディア誌,Vol. 53,No.8(1999)
26) 岡隆一. セル特徴を用いた手書き漢字認識の研究. 電子技術総合研究報告, Vol. 834, 1983.
27) 萩田紀博, 内藤誠一郎, 増田功. 大局的・局所的方向寄与度特徴による手書き文字認識方式. 電子情報通信学会論文誌, Vol.J66-D, No. 6, pp.722-729, 1983.
28) 斉藤泰一, 山田博三, 森俊二. 手書文字データべ−スの解析(iii). 電総研彙報, Vol. 42, No. 5, pp.385-434, 1978.
29) 斉藤泰一, 山田博三, 山本和彦. JIS第1 水準手書き漢字デ−タベ−スETL 9 とその解析. 電子情報通信学会論文誌, Vol. J68-D, No. 4, pp.757-764, 1985.
30) 萩田紀博. 21世紀の文字認識研究に期待すること. 電子情報通信学会技報, Vol. PRMU98-149, pp.103-110, 1998.
31) Michael Kass, Andrew Witkin, and Demetri Terzopoulo. Snakes: Active contour models. International
Journal of Computer Vision, Vol. 1, No. 4, pp. 321-331, 1988.
32) 松下博, 森吉弘, 乾敏郎. スケルトンを用いた階層的形状記述およびニュ−ラルネットによる階層的形
状識別. 電子情報通信学会論文誌, Vol. J73-D-II, No. 6, pp.812-819, 1990.
33) M. Nagaishi. Image processing system. U.S. Patent, 5365600, 1994.
本ページの原典
長石道博: "視覚の誘導場によるパターン認知の研究", 豊橋技術科学大学 博士論文 乙第142号 (2000)
[学位論文]
|
【付録】 弾性エネルギーの計算
ある等ポテンシャル面における,弾性エネルギ U 1,U 2 の計算方法を 図11 を例に説明す
る.図11 のように,反時計回り並んだ n 個の点で構成される等ポテンシャル線 A を等ポテンシャル線
B に一致させるとする.図11 (b) は点 i 近傍の変位を示した図である.図11 (b) の要領で,等ポテンシャル線 A の点 i から法線方向上にある等ポテンシャル線 B までの変位 u(i) を求める.変位 u(i) = u( x(i), y(i) )
だから,U の偏微分は次の差分に直して計算できる.
|

|

図11 変位方向の求め方
|
【付録】 法線方向の決定
誘導場の認識モデルにおいて,式(4.1),(4.2) の弾性エネルギ U 1,U 2 を求めるには,
最初に等ポテンシャル線の輪郭線を求め,変位方向である法線方向を決定する.しかし,デジタル画像の誘導
場から,等ポテンシャル面の輪郭線を直接求めると凹凸が大きく法線方向に大きな誤差が生ずる恐れがあ
る.
そこで,誘導場自身を平滑化後,誘導場からポテンシャル値ごとに等ポテンシャル面を得て輪郭線を抽
出する.誘導場の強さは指数関数的に変化するので,最初にメジアンフィルタ,続いて8 近傍濃度の荷重平均により平滑化した.
法線方向を決定する際,注目点近傍の輪郭線が滑らかな必要があるため,抽出した輪郭線自体をガウス
フィルタによる畳込み積分で平滑化した32).輪郭線の元々の形状が失われない範囲で経験的にσ = 4 (dot)
とした.
法線方向を注目点近傍のみを参照する差分法により高精度で求めるのは難しい.そこで,図12 のよう
に,輪郭線 S 上の注目点 P を中心に 5 × 5 dot の領域の輪郭線に接する接線を,点 P を原点とする Hough
変換で推定する方法33) を用いて求め,法線方向 n を決定した.
|

図12 Hough 変換による法線方向の推定
|