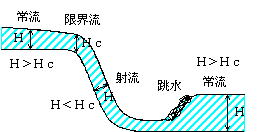
棳傟偺庬椶
忢棳偲幩棳丄尷奅棳
丂愳偺棳傟傪娤嶡偟偰偄傞偲丄備偭偨傝偲偟偨棳傟偲偄傢備傞媫棳偺棳傟偑偁傞丅偦偟偰丄媫側棳傟偺廔揰晹偱偼丄塓傪姫偄偰悈埵偑忋徃傪婲偙偟偰偄傞偺偑娤嶡偱偒傞丅懍偄棳傟偑壓棳偺棳傟偵撍偭崬傫偱峴偔傛偆偵傕尒偊丄傑偨丄壓棳偺悈埵偑崅偄偺偵忋棳偺悈埵偵塭嬁傪梌偊偢丄悈柺偑晄楢懕偲側傞偺偼晄巚媍偵姶偠傜傟傞丅
丂偙偺偙偲偼丄偍晽楥偵悈傪擖傟偰偄傞偲偒側偳偵傕娤嶡偱偒傞丅
丂偙偺尰徾偼丄捈姶揑偵棳懍偺堘偄偵傛傞傕偺偲偄偆婥偑偡傞偑丄丂偙偺尰徾傪丄棟榑揑偵専徹偟偰傒傞丅
| 棊嵎岺 |  |
侾丂斾僄僱儖僊乕丂
| 丂塃恾偵偍偄偰丄悈楬彴傪婎弨偲偟偰丄儀儖僰乕僀偺掕棟傪奐悈楬偵摉偰偼傔傞偲丄悈楬彴偐傜僄僱儖僊乕慄傑偱偺崅偝傪俤偲偡傟偽丄師偺傛偆偵側傞丅 丂丂丂棳懍 丂丂丂 丂丂偙偺俤傪斾僄僱儖僊乕偲偄偆丅 丂丂 丂丂悈怺俫丂偼丄棳傟偺拞偺擟堄偺揰俹丂偵偍偗傞悈楬彴偐傜偺埵抲僄僱儖僊乕倓丂偲揰俹丂偵偍偗傞埑椡悈摢乮P/倵乯偺崌寁偲側傞丅 丂曗懌丂P亖兿倗倛丄丂倵亖兿倗丄丂P/倵亖倛 |
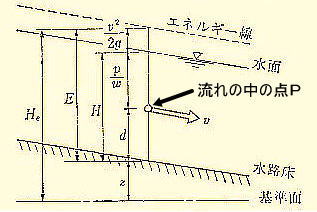 |
丂丂曗懌愢柧
丂斾僄僱儖僊乕偼丄扨埵懱愊廳検偵偮偄偰悈偺帩偮慡僄僱儖僊乕偱偡丅
丂偙偙偱丄悈棟妛偱偺僄僱儖僊乕曐懚偺朄懃傪峫偊偰傒傞丅
丂崅峑偺暔棟偱妛廗偟偨僄僱儖僊乕曐懚偺朄懃偼丄扨埵帪娫偵堏摦偡傞悈偺幙検丂倣亖乮枾搙乯亊乮懱愊乯亖兿丒倎丒倴丂偐傜師昞偺傛偆偵惍棟偝傟傞丅
丂儀儖僰乕僀偺掕棟偼丄悈棟妛偺昞尰傪扨埵帪娫偵堏摦偡傞悈偺廳検亖倂亖倣倗亖兿丒倎丒倴丒倗丂偱妱偭偨傕偺偱丄扨埵懱愊廳検偺奺僄僱儖僊乕偺戝偒偝傪昞偟傑偡丅偙傟偼丄挿偝偺扨埵傪帩偪乽悈摢乿偲偄偆丅
丂兿丗枾搙丄a丗棳悈柺愊丄v丗棳懍
丂斾僄僱儖僊乕偼丄儀儖僰乕僀偺掕棟傪奐悈楬偵摉偰偼傔偨傕偺丅
| 暔棟偺昞尰 | 悈棟妛偺昞尰 | 丂丂丂儀儖僰乕僀偺掕棟 | ||
| 塣摦偺僄僱儖僊乕 | 1/2亊乮幙検乯亊乮懍搙乯俀 | 1/2亊乮兿丒倎丒倴乯亊乮円乯俀 | 侾乛俀亊乮侾乛倗乯亊乮倴乯俀 | 懍搙悈摢 |
| 埵抲偺僄僱儖僊乕 | 乮幙検乯亊倗亊乮崅偝乯 | 乮兿丒倎丒倴乯亊倗亊倸 | 倸 | 埵抲悈摢 |
| 埑椡偺僄僱儖僊乕 | 乮埑椡乯亊乮嫍棧乯 | 乮倫丒倎乯亊乮倴乯 | P乛倵 | 埑椡悈摢 |
| 崌寁 | 堦掕 | 堦掕 | 丂丂丂丂丂丂丂丂丂堦掕 兿丒倎丒倴丒倗亖W 偐傜嵍幃傪惍棟 |
|
俀丂斾僄僱儖僊乕偲尷奅悈怺
丂
丂乮侾乯丂斾僄僱儖僊乕偲悈怺偺娭學
丂斾僄僱儖僊乕傪挿曽宍抐柺偵偮偄偰昞偡偲師偺幃偵側傞丅
丂丂![]() 丂丂丂乮俆-俆-俀乯
丂丂丂乮俆-俆-俀乯
丂丂偙偺幃傪丄棳検俻傪堦掕丄枖偼丄斾僄僱儖僊乕俤傪堦掕偲偟偰僌儔僼偵昞偡偲丄師偺傛偆偵側傞丅
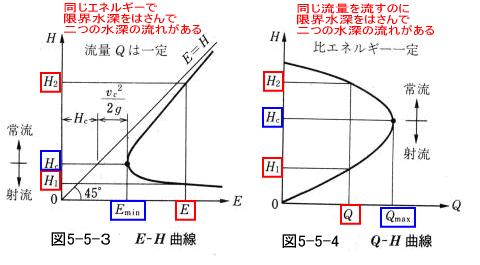 |
丂偙偺擇偮偺僌儔僼偐傜丄棳検俻偑堦掕偱偁偭偰傕丄悈怺偑曄壔偡傟偽偄傠偄傠側斾僄僱儖僊乕傪傕偮棳傟偑偁傞偙偲偑傢偐傞丅傑偨丄堦掕偺斾僄僱儖僊乕傪梌偊偨偲偒丄擇偮偺悈怺俫侾偲俫俀偑懚嵼偡傞偙偲偑傢偐傞丅
丂俤亅俫嬋慄偱丄斾僄僱儖僊乕偑嵟彫乮俤倣倝値乯偺偲偒偺悈怺傪尷奅悈怺偲偄偆丅
乮俀乯丂尷奅悈怺丄尷奅棳懍傪媮傔傞丅
丂尷奅悈怺傪媮傔傞偵偼丄尷奅悈怺偑斾僄僱儖僊乕傪嵟彫偲偡傞悈怺偱偁傞偙偲偐傜
丂![]() 丂偺偲偒偺悈怺傪媮傔傟偽椙偄丅
丂偺偲偒偺悈怺傪媮傔傟偽椙偄丅
丂挿曽宍抐柺偺応崌丄偙傟傪夝偔偲丄壓偺昞偱帵偡傛偆偵丄
丂丂丂丂丂丂丂丂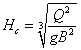 丂丂乮俆-俆-俁乯
丂丂乮俆-俆-俁乯
丂偲側傞丅
丂傑偨丄![]() 丄
丄![]() 偐傜丄
偐傜丄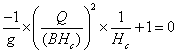
丂偙傟傪惍棟偟偰丄![]() 丂
丂
丂
丂偙傟偐傜丄![]()
丂偲側傝丄丂偙傟偼丄尷奅悈怺偺偲偒偺棳傟偺懍偝丄尷奅棳懍
丂丂丂丂丂丂丂![]() 丂丂丂丂乮俆-俆-係乯
丂丂丂丂乮俆-俆-係乯
丂傪帵偟偰偄傞丅
| 僠僃僢僋 丂尷奅悈怺丂俫們丂偼丄 丂尷奅悈怺偼丄恾俆-俆-係偱傢偐傞傛偆偵丄斾僄僱儖僊乕丂俤亖堦掕偺忦審偺傕偲偱丄棳検丂俻丂傪嵟戝偲偡傞悈怺偲側傞丅 丂幃乮俆-俆-俀乯傪丂俫丂偱旝暘乮崌惉娭悢偺旝暘乯偡傞偲丄 丂偙傟傪惍棟偡傞偲丄 丄 丂偟偨偑偭偰丄 丂 丂尷奅悈怺傪媮傔傞応崌偺堦斒夝偼丄 丂 丂偺夝偲側傞丅 |
||||
尷奅悈怺偺夝傪媮傔傞僾儘僾儔儉梡寁嶼幃惍棟昞
| 悈楬抐柺 | 尷奅悈怺偺寁嶼幃 |
| 挿曽宍抐柺 | 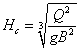 |
| 戜宍抐柺 | 丂偙偙偱偼丄幃乮俆-俆-俆乯偐傜媮傔偰傒傞丅丂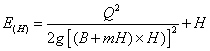 丂幃乮俆-俆-俆乯偐傜丄 丂 丂 丂偟偨偑偭偰丄偙傟傪幃乮俆-俆-俆乯偵戙擖偡傞偲丄 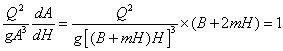 丂偲側傞丅丅 丂 丂偙傟傪丂俫們丂偵偮偄偰惍棟偡傞偲 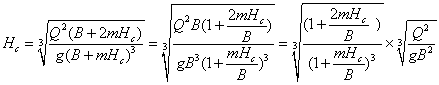 丂偲側傞丅 丂偙偺応崌丄椉曈偵曄悢傪娷傫偱偄傞偺偱丄拃師嬤帡朄摍偺悢抣夝朄偵傛傝夝傪傕偲傔傞丅 |
| 墌宍抐柺 | 丂偙傟傕丄幃乮俆-俆-俆乯偐傜媮傔偰傒傞丅丂 丂 丂丂丂丂丂丂丂丂丂丂丂傑偨丄丂 丂 丂 丂 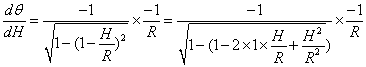 丂丂丂丂 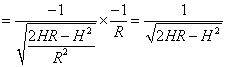 丂 丂偟偨偑偭偰 丂 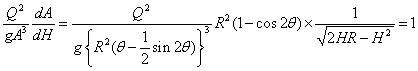 丂傪枮懌偡傞丂俫丂偑夝偲側傞丅 丂偙偙偱丄 丂 丂 丂 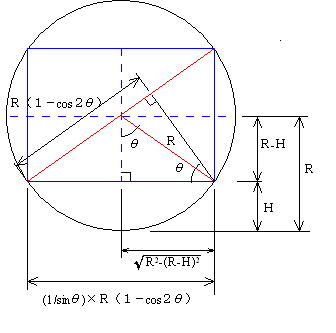 丂偙偺偙偲偼丄 丂丂 丂偙傟偵傛傝丄師偺庤弴偱夝傪媮傔傞丅 丂傑偢丄壖偺夝偲側傞悈怺傪梌偊傞丅 丂偙偺壖偺悈怺偵傛傝丄堦師夝傪媮傔傞丅 丂 丂仸侾 丂 丂丂丂丂丂丂丂丂 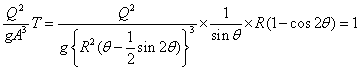 丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂 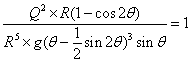 丂丂丂丂丂丂丂丂 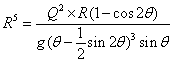 丂 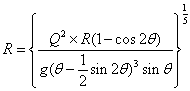 丂 丂 |
俁丂僼儖乕僪悢
丂挿攇偺揱攄懍搙偼丄![]() 偱梌偊傜傟傞偑丄偙偺挿攇偺揱攄懍搙偲棳懍偺斾傪丂僼儖乕僪悢丂俥倰丂偲偄偆丅
偱梌偊傜傟傞偑丄偙偺挿攇偺揱攄懍搙偲棳懍偺斾傪丂僼儖乕僪悢丂俥倰丂偲偄偆丅
丂丂丂丂丂丂丂丂![]() 丂丂乮俆-俆-俇乯
丂丂乮俆-俆-俇乯
丂
丂丂丂丂丂丂丂丂偙偙偱丄俢丗悈棟悈怺乮倣乯丂俢亖俙乛俿丂
丂丂丂丂丂丂丂丂丂丂丂丂丂俙丗捠悈抐柺愊乮倣俀乯
丂丂丂丂丂丂丂丂丂丂丂丂丂俿丗悈柺暆乮倣乯
丂悈怺偑丄尷奅悈怺偲側偭偨応崌偺僼儖乕僪悢偼丄![]() 丂偲側傞丅
丂偲側傞丅
丂偙偺偙偲偐傜丄忢棳丄幩棳丄尷奅棳傪丄尷奅悈怺媦傃尷奅棳懍丄僼儖乕僪悢偵傛偭偰敾暿偡傞偲丄師偺傛偆偵側傞丅
| 悈怺 | 棳懍 | 僼儖乕僪悢 | |
| 忢棳 | |||
| 幩棳 | |||
| 尷奅棳 |
係丂尷奅悈怺傪媮傔傞
壽戣侾丂挿曽宍乮嬮宍乯抐柺悈楬偺尷奅悈怺丄尷奅棳懍傪媮傔傞丅
寁嶼偺庤弴
庤弴侾丂寁嶼偵昁梫側丄悈楬抐柺宍忬丄棳検偺僨乕僞乕傪惍棟偡傞丅
丂丂丂丂丂悈楬暆丄棳検傪媮傔傞丅
庤弴俀丂尷奅悈怺傪丄幃乮俆-俆-俁乯偐傜媮傔傞丅
庤弴俁丂尷奅棳懍傪丄幃乮俆-俆-係乯偐傜媮傔傞丅
丂丂
寁嶼
壽戣俀丂戜宍抐柺悈楬偺尷奅悈怺丄尷奅棳懍傪媮傔傞丅
寁嶼偺庤弴
庤弴侾丂寁嶼偵昁梫側丄悈楬抐柺宍忬丄棳検偺僨乕僞乕傪惍棟偡傞丅
丂丂丂丂丂悈楬暆丄悈楬朄偺岡攝丄棳検傪媮傔傞丅
庤弴俀丂師偺幃偐傜丄拃師嬤帡朄偱媮傔偰傒傞丅
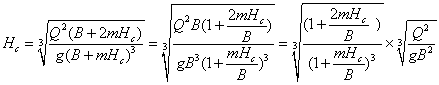
丂丂拃師嬤帡朄偺椺戣
丂丂悈楬偺掙暆丂俛亖俀.侽倣丂朄岡攝丂倣亖侽.俆丂棳検丂俻亖俉丏俆倣3/倱
丂丂偺偲偒
丂丂丂丂丂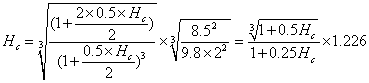
丂丂俫們佭1.2偲壖掕偟偰塃曈傪寁嶼偡傞偲丅
丂丂戞侾嬤帡夝丂俫們1亖1.103丂傪摼傞丅
丂丂偙傟傪傕偆堦搙戙擖偟丄戞俀嬤帡夝丂俫們俀亖1.113丂傪摼傞丅
丂丂摨條側庤弴傪孞傝曉偟丄戞俁嬤帡夝丂俫們俁亖1.112丂丂戞係嬤帡夝丂俫們係亖1.112丂丂偲側傝
丂丂俫們亖1.112丂偵廂懇偡傞丅
丂丂偟偨偑偭偰丄俫們亖1.112丂傪摎偊偲偡傞丅
寁嶼
壽戣俁丂墌宍抐柺悈楬偺尷奅悈怺丄尷奅棳懍傪媮傔傞丅
寁嶼偺庤弴
庤弴侾丂寁嶼偵昁梫側丄悈楬抐柺宍忬丄棳検偺僨乕僞乕傪惍棟偡傞丅
庤弴俀丂師偺幃偐傜丄拃師嬤帡朄偱媮傔偰傒傞丅
丂丂丂丂丂壖偺尷奅悈怺偲偟偰丄俫們侾佭俼乮擟堄偺抣乯傪梌偊傞丅
丂丂丂丂嘆丂![]()
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 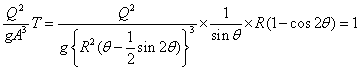 丂丂 偐傜
丂丂 偐傜
丂丂丂丂嘇丂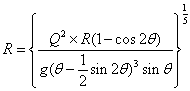
丂丂丂丂嘊丂![]()
丂丂丂丂嘋丂![]() 丂偲偟偰丂
丂偲偟偰丂![]() 丂偲側傞傑偱丂嘆丂偐傜丂嘋丂傑偱傪孞傝曉偟寁嶼偡傞丅
丂偲側傞傑偱丂嘆丂偐傜丂嘋丂傑偱傪孞傝曉偟寁嶼偡傞丅
丂寁嶼