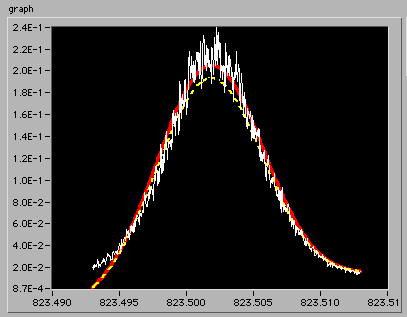
さて、前回紹介したプログラムを宮本さんに送ったのですが、10日後にデータによって回帰の精度が低いことがあるとの連絡を受けました。前回は生データを2個送っていただいていたのですが、今回さらに1個添付してもらいました。たしかに今一つのできのようです。黄色の破線は初期値、赤い実線は回帰結果なのですが実データとのずれがあります。

また、解析対象の性質上1次成分が存在しない条件で回帰できるようにしたい、ということでした。
プログラムの見直しは、初期値を求める部分から始めました。プログラムの動作時間から考えても一度しか処理しない部分なので多少時間がかかっても全体としては微々たるものだろうという読みもあります。
前回は、「移動平均をかけようかなとも思いましたが、General Polynomial Fit.viを使うことにしました。ガウス回帰をするために、備え付けの回帰プログラムを使う。なかなかよい発想だと思いませんか?」と、調子に乗ってしまいましたが、General Polynomial Fit.viの5次近似ではガウス曲線の裾近くまで得られているデータには露骨なまでに具合が悪くて、素直にごめんなさいです。
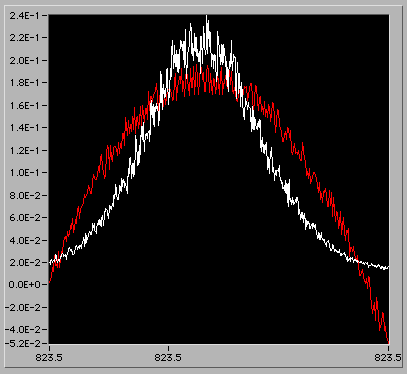
気を取り直して移動平均を使うことにしました。
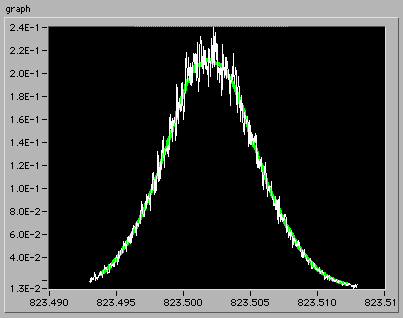
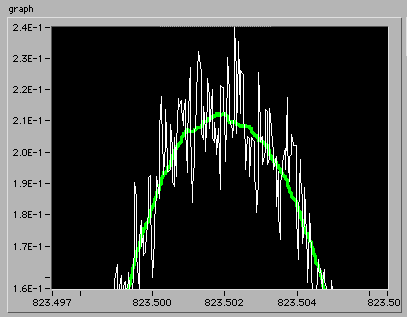
なかなかよさそうに見えますが、先端を拡大すると結構でこぼこです。生データよりははるかに扱いやすそうなのでこれで行くことにしました。
ダイアグラムは下のようなものです。データ数が平均化の幅から1引いた分だけ少なくなるので、対応するxも平均化の幅の半分だけずらしています。
さて、回帰のベースとなるのは下の回帰式ですが、ここにも基本的な判断ミスがありました。
y=a * exp ( - b * (x - c) ^2) + d * x + e
1次関数部分が原点(0,0)基準の表記になっています。たいした問題ではないと思っていましたが、原点から遠く離れた場所にデータの中心がある今回のような場合は、dの誤差によりガウス曲線の中心部ではeがばらついてしまいます。今回は下の回帰式に変更することにしました。これで、eはガウス曲線の中心部でのシフト量として考えることができます。
y=a * exp ( - b * (x - c) ^2) + d * (x - c) + e
ガウス関数の幅についてもプログラムの中で使うことが多かったので、変更して最終的には以下の式にしました。
y=a * exp ( - {(x - c) / b }^2) + d * (x - c) + e
次は平均化処理したデータへのガウス曲線のあてはめです。
ガウス曲線の裾野までデータがあればaやeを決めるのは簡単ですが、途中で途切れている場合、例えば、高さの1/e以上しかデータがないときには難しくなります。結局、途中で途切れたデータから裾野がどこにあるのか予測しなくてはいけません。前回はデータの中でyが最小の部分を裾野と仮決めしてaの初期値を決めていましたが、せっかくの機会ですからもう一歩、予測精度を上げることにしました。
見通しを良くするために y=a * exp ( - {x/ b }^2) で考えてみます。
x=bの時には y=a*exp(-1)で、だいたい0.37a になります。
x=b/2の時には y=a*exp(-1/4)で、だいたい0.78aです。
x=b/3の時には y=a*exp(-1/9)で、だいたい0.89aです。
このようにガウス関数のプロポーションは決まっているので、裾野が見えなくてもガウス曲線の上2/3ぐらいがあれば、a, b, c, eを求めることができます。
y=a * exp( - (x/b)^2 ) + eという関数において、適当なkを考えて
x=k の時、y=y1、
x=k/2 の時、y=y2、
x=k/3 の時、y=y3とします。
このとき
((y2-e)/(y1-e))^(4/3) = ((y3-e)/(y1-e))^(9/8)
が成り立つので、これを満たすようなeを近似的に求めることにしました。そのあとで、代入によって順次 b, a を求めます。
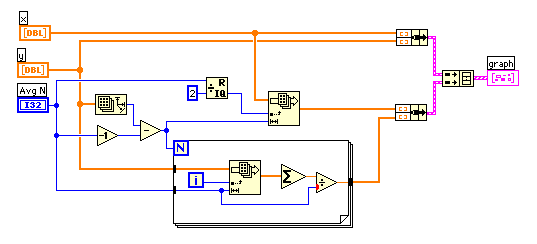
次のダイアグラムでy1, y2, y3を求めて、サブVIのcalc abe.viで計算を行っています。とりあえず、kはy軸の変化幅の1/eの高さにおけるx方向の幅ということにします。('k'はcalc
abe.viアイコンの左の4番目に入っていくデータです。)
y2とy3を求めるのが厄介なわけですが、今回はy1の高さで切り取った部分の中央にピークがあると仮定して、スムーズ化したデータをピーク位置で2分割して前半を反転して平均化します。配列同士の加算では小さいほうのサイズで出力されるので、この場合は好都合です。
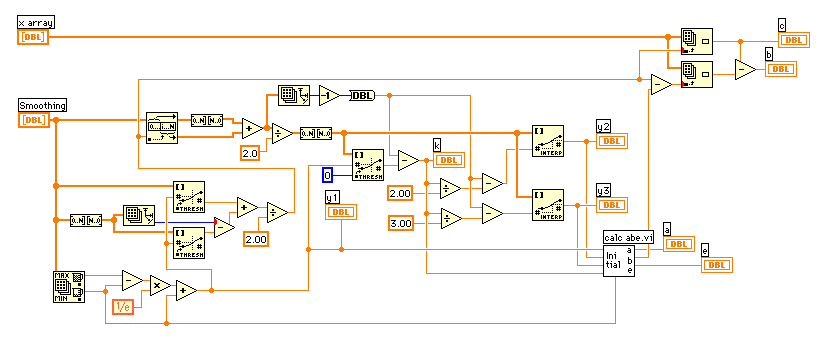
下がa, b, e の計算を行うviです。ホワイルループの中でMinimumから少しづつ小さくしていきます。
((y2-e)/(y1-e))^(4/3) と((y3-e)/(y1-e))^(9/8) の差をとって絶対値が増加するまでループを回します。eが求まれば、後は代入でaとbを求めることができます。
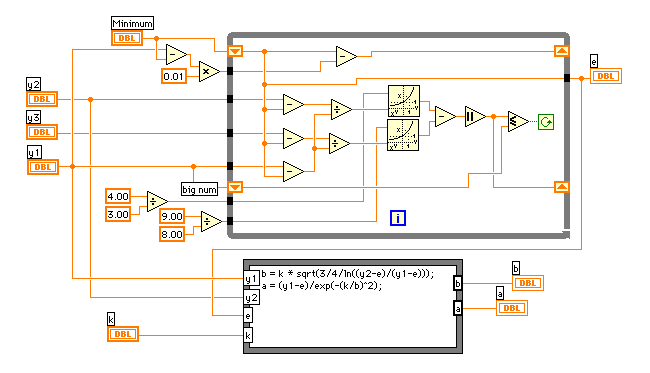
これで初期値はかなり近いところに合わせることができました。
フロントパネルでは1次の項や定数項をチェックボックスでOFF/ONすることができます。これは初期値を0にして回帰しているだけで両方OFFにすれば回帰する係数が3個ですから、総当たりで8回計算しても、L8の直交表を使っても同じ計算量です。複雑になっている分だけL8の直交表の方が不利になります。
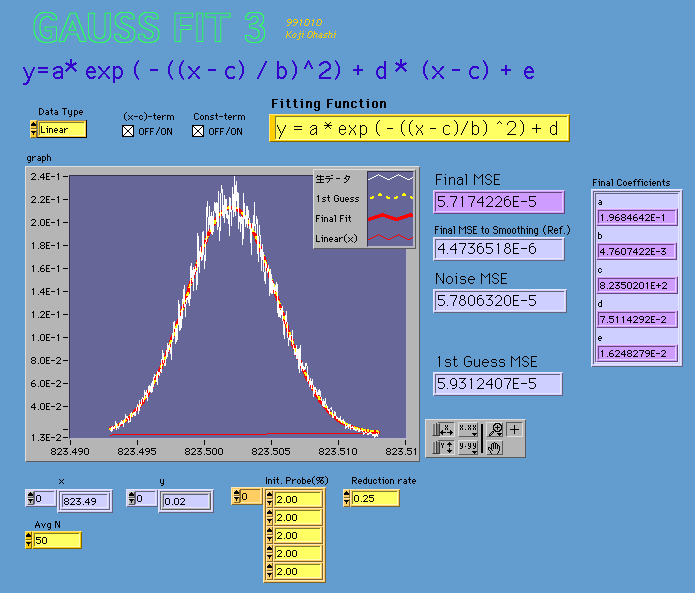
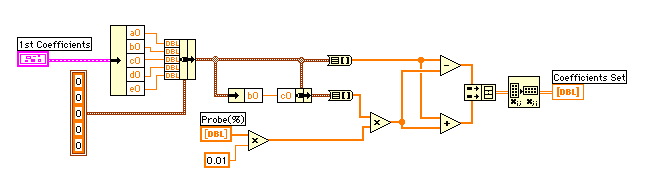
係数のセットを決めているサブviでバグがあったのも回帰を悪くしている原因だったことを白状しておきましょう。前回のダイアグラムと比較してみて下さい。
では、予想以上に長くなってしまいましたがこの辺で一区切りにしましょう。
99.010.24 大橋 康司
ohashi@mac.email.ne.jp