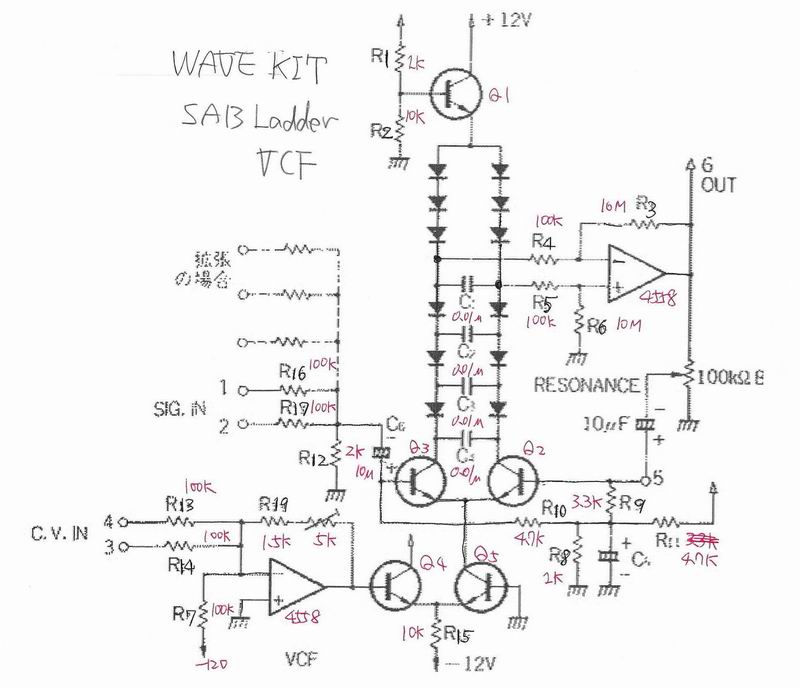
*1:
ご利益を受けないと言うのはうそです。 そうであればわざわざ負荷をdiodeにする意味
が無く負荷が抵抗では単なるVCAになってしまいます。 ladderの負荷が単に抵抗であれば制御電流のEXPO特性そのままになってしまうところをdiode負荷のおかげでそうはなりません。
実機での測定
filterとしてでなくAMPとしてのゲインをはかるため、filterの4っのCをはずして信号波形の電圧振幅を測定。(OP AMP OUT)
|
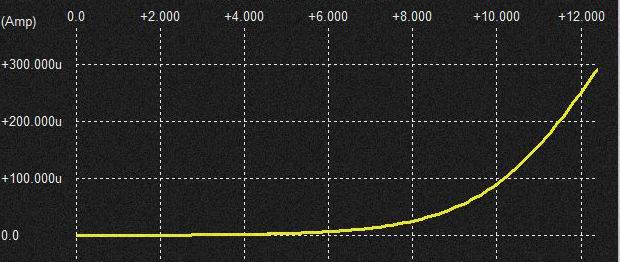
まずはladderに何もつながない状態(OP AMP接続無し)にしてCV=0から12Vまで可変した時のdiode負荷での電圧振幅を測定。 結果はほぼ全域にわたって振幅変化なし。 正確には CV=12Vに近づくにつれてで若干振幅の増加が見られる程度。.....(なぜ上昇が見られるのかわからず。)
|
次に反転側と非反転側の電圧振幅の違いを見るためにdiode負荷の位置で電圧を測定。
(カップリングCなし、抵抗直付け(OP AMP付け))
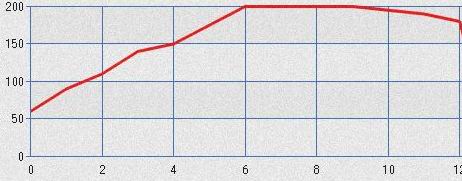
非反転入力側
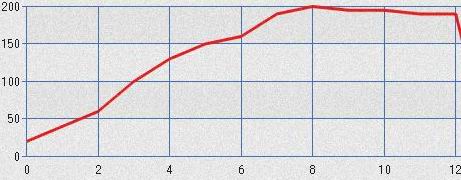
反転入力側
入力インピーダンスの関係から反転側のゲインロスが大きいのは予想できましたが、非反転側でもテイル電流の小さい(filterとしてはFcが低い)場合のゲインロスがかなりあります。
次にはカップリングのCあり / 無し時の信号電圧振幅特性の差を調べる。(OP AMP OUT)
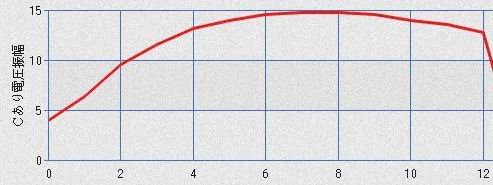
カップリングのCあり時の信号電圧振幅特性
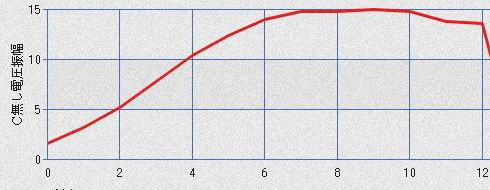
カップリングのC無し時の信号電圧振幅特性
テイル電流が小さい場合、Cがあることにより改善されていますが。
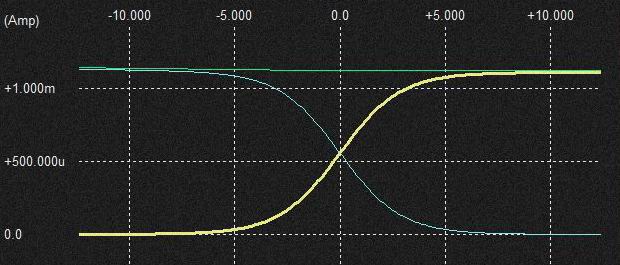
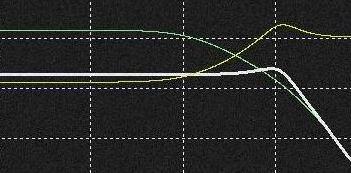
シミュレータでCVを変化させた時の3本のDiodeの電圧を測ってみました。(FilterのCap.は外して)

深緑; OPampの非反転端子側のLadder Diode負荷(3本)
白: OPampの反転端子側のLadder Diode負荷(3本)
反転入力側は低域で振幅が低下しています。(CV=1..7V)が非反転側はロスが無いようで測定結果と違います。 測定が悪いのか。
OPAMPのカップリングのCap.を入れた場合と入れない場合の反転入力側のDiode負荷の信号振幅

深緑; Cap.なし
白: Cap.あり
白く見えるぶぶんが差分ですが、低域で振幅が若干低下していますが左右のLadderとの差ほどは無し。(CV=1..4V)
最後に問題のresonance発振周波数と電圧振幅の関係を以下にしめします。

Filter発振( カップリングCあり時/ R15=3.3K / filter C=0.047uf )
| CV(V) | 発振周波数(Hz) | 電圧振幅(V) |
| 00 | 022 | 0.34 |
| 01 | 035 | 0.58 |
| 02 | 060 | 0.9 |
| 03 | 108 | 1.05 |
| 04 | 211 | 1.2 |
| 05 | 400 | 1.2 |
| 06 | 735 | 1.3 |
| 07 | 1.4K | 1.3 |
| 08 | 2.8K | 1.4 |
| 09 | 4.6K | 1.5 |
| 10 | 8.8K | 1.7 |
| 11 | 11.9K | 1.9 |
| 12 | 16.4K | 2.25 |
* 0から7VくらいまではCあり時のAMPの振幅特性を反映している感じ。
* それ以降はさらに発振振幅が伸びる条件が加わるような感じ
* 測定が悪いのかOct/Vになっていない区間が多いですが概要はつかめるかと。
* 始めに書いたように回路上厳密にはEXPO特性にはなりませんがその影響か。
|
ここで新たな疑問が生じてしまいました。 AMP特性は平坦なのに高域にいくにしたがってなぜ発振振幅が増加するのかという問題。 発振ということではそれ以前にどうして安定して発振できているかをわかる必要があります。
|
負帰還型VCFの正帰還発振
このfilterの発振は CR filter 4段接続による位相発振動作と同じです(*1)。 帰還ループ内にBPFが構成されループ内のfilterのゲインロスを補う形でAMPが挿入され、閉ループゲインが1以上になれば発振します。
*1: 厳密には電圧入力型のfilterと定電流入力型のfilterという違いはあります。
(Tr./DiodeLadderともに負帰還タイプですが定電流型はTransisterLadderでDiode Ladderは電圧入力型です。)
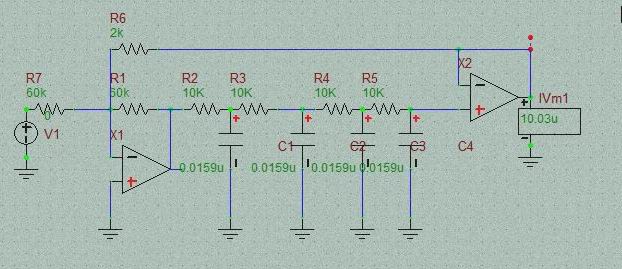
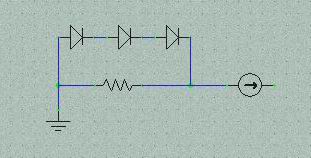
上のような回路を考えてみました。
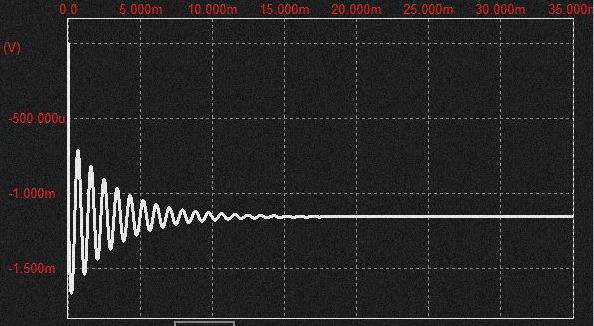
Rf=30Kで帰還のゲインは15倍
この状態ではまだ発振できず減衰振動となります。FilterのFcでそれ以上、減衰しているのでしょう。ちょうどインパルス共振によるanalog DRUMの波形と同様な波形。 閉ループゲイン1以下なのでループするごとに振幅が減衰。
|
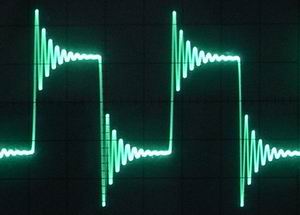
この波形どっかでみた記憶がと思いきやresonanceを上げた時波形に重畳されるあの形でですね。(下図参照)
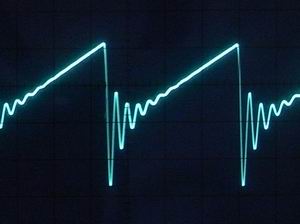
|
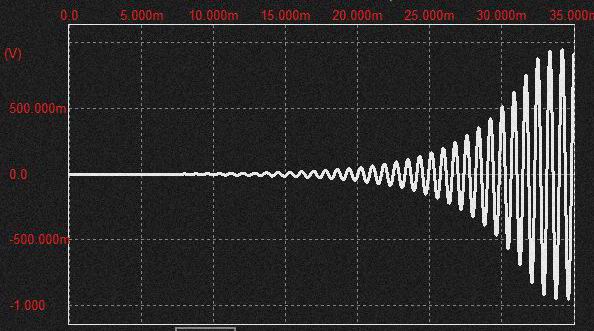
Rf=40Kで帰還のゲインは20倍
でやっと上のグラフと違って初段の OPAMPの出力が後の filterのゲインロスより大きくなってゲインロスが解消されたので発振できた。 すなわちループゲイン 1以上。
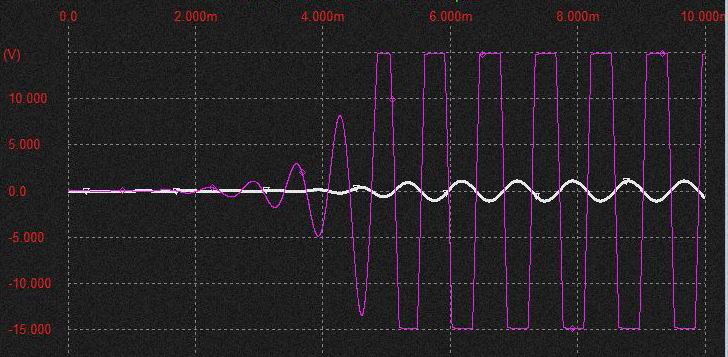
赤: 初段のOP AMP
白: 後段のBuffer出力(上の2っの波形と同様の出力)
上図は初段の OP AMP出力と最終段のOP AMPの出力の変化を示したもの。 初段のOP AMPの出力が電源電圧まで達し飽和したところで発振波形振幅は安定する。 最終段のOP AMPの出力は初段と異なり歪んでいない。
4段filterで位相が180度回転した結果を逆相で戻して360度にするということはFcではあくまで正帰還になっているので信号振幅はいけるとこまで増大してしまうのは正帰還タイプのfilterと違いはないということです。 ただ最終出力段は4っのfilterの後なのでゲインが低下していてクリップしていないというだけ。 SIN波がクリップして矩形波になり、発振周波数と同じFcの4段LPFで再度SIN波を得る(*1)。 SIN波生成の手助けはLPFとHPFで構成された同じF0のBPFという構成。
*:
Fcでは位相差が1段あたり45度なので4段で位相差180度。NFBで正帰還
通過帯域ではFcから離れるほど位相差は少なくなるのでNFBをかければHPF特性となる
遮断帯域ではGAINが小さいのでNFBしても影響はあまりない
帰還ループ内にBPFが構成されるから一点(単一周波数)でSIN発振できる。
この例のfilterの発振振幅のリミッタは OP AMPの電源電圧なので OP AMPの電源電圧を上げれば発振振幅が大きくなります。 ではladder VCFのリミッタはどこ存在しどうやって発振振幅を一定にすることができるのかと言うことになります。
*1: 発振状態ではLPFと言うよりはBPFとして動作。
ちなみにFcのBPFにFcの周波数の矩形波が入力されるので出力はSIN波になる。
ladder VCFの振幅リミッタはどこに
これは正帰還発振の振幅上昇がある地点で止まる理由を考えるということです。 負帰還による発振においても発振振幅増大の暴走を止める為のリミッタは必要でシミュレーション例の位相発振においては初段の OP AMPの出力が電源電圧まで達した所で発振振幅の上昇が止まって平衡する。(1点で止まって動かないので帰還量を増やしても同じ発振振幅しか出ない。)
diode ladderにおいてはリミッタは resonanceの戻りが入る差動アンプの入出力特性(電圧 -- 電流特性)にあると思われます。 ladderの場合は入力に戻す帰還量に応じて発振振幅が連動して上昇している区間がある。 さらに帰還量を上げるともうそれ以上、上がらなくなる。 これは差動アンプの最終クリップの点にいたる少し前のLOG特性付近での動作と一致する。 これとCVが低い時は発振振幅が小さいことの関係があるのかないのか?。
ループゲインが1以上あればループを繰り返すことで序所に振幅は増加する。 帰還量が少ない場合は増加量がすくないだけで両者ともいける最大値まで達しそうであるが実際は帰還量が少ない方が最終振幅は小さい。 考えられることは、入出力特性がリニアではないので LOG領域にさしかかると帰還ループが重くなるというかおそらく抵抗が生じて平衡するのでは?。( 坂道で自転車をこぐのが大変になるのと同じ原理か ) もしくは帰還量が少ない方がfilterでのロスが大きいのか?
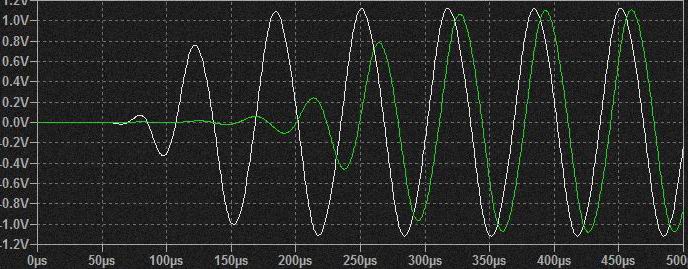
resonance量 1/2 1/3 1/4
同一CV時、帰還量の大小で振幅は変化。

同一CV時、Resonance VRがMAXに近ければVRの差があっても最終的にはほぼ同じ振幅になるように見えるのは差動対の電流特性を反映してのマジック?.
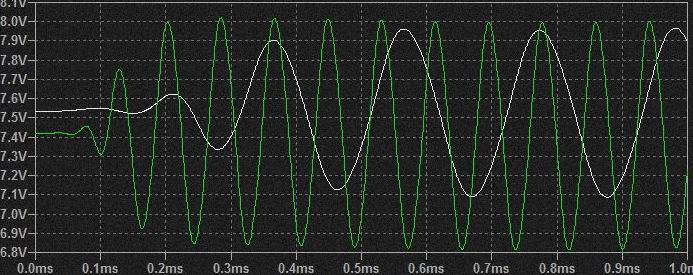
白: CV 小
緑: CV 大
CV値が同じでResonance VRの値によって振幅が変化するのは当然ですがCV値が小さければ帰還量最大でも最終振幅はCV値が大きい時ほど大きくなれない。CV値の大小に応じてテイル電流/2 の値すなわちLimit値は変化しているわけなので同じになってもよさそうですが。
この場合正帰還ループなので発振周波数が高い方が単位時間あたりの積算量は増えそうなのでそうなれば立ち上がりは急になる、すなわち振幅が大きくなるという単純原理のように見えます。
CV=12V時はもちろんCV=0V時点の比較的小さい発振振幅(300mV)でもQ2のベースに入力される電圧振幅は リニア領域を超えてLOG領域に入っている。(クリップの度合いが違うだけ) すなわち電流の最大値までは振幅の大きさはどちらもある。
* 各シミュレーション波形

黄色: CV=12V時の発振電流波形(差動ペアの出力)
白色: CV=0V時の発振電流波形(差動ペアの出力)
正帰還の発振信号がQ2に入力されると強くオーバードライブされて出力は矩形波になっている。 これが発振周波数と同じFcの4段LPFというか実際の動作は同じF0のBPFを通ると SIN波となって再度 Q2の反転入力に印加される。

両者ともMAX値になっているが波形が違うので4段のCR LPFを通した後のSIN波波形は矩形波の方が振幅が大きい。この差が正帰還され振幅差が発生するのだろうか?。
|
手持ちのsynthでdiode ladderは無いのでtransistor ladderの MS404のVCFの発振振幅を測ってみました。

transistor ladderのMS404のVCF発振の振幅グラフを下に示します。

WAVE KITほどは変化が少なく最小値と最大値の差が2倍程度ですが傾向は似ていますのでladder VCF独特の物のようです。 MS404は信号の取り出しに OP AMPのbufferを使っているので低域の減衰が小さいのだと思われます。
MS404ではladder出力から resonanceで信号を反転入力に戻す際の差動AMPの電圧ゲインは15倍であり、WAVEKIT(定数変更後)の90倍に比べて1/6になっています。 transistor laderの cutoffでのゲインの落ち込みがdiode ladderに比べて 1/4以下なのでこの値は妥当な物なのでしょう。
このこともあって resonanceを上げても通過帯域の落ち込みが少なく、発振直前でもresonance=0の1/2程度しか振幅が低下していないのはとても良いことだと思います。 MS404ではladder 出力をbufferで受けた語、resonance用のAMPとVCF出力用のAMPが別系統になっています。
* MS404のVCFは基本 MOOG rogueのコピーです。

*MS404Tr.Ladder VCF
LadderのあとはBuuferが付いてその後に差動入力のCA3080をVCAとして使い、パラってresonance用の差動AMPという構成。VCAの電流出力の後は抵抗による電圧化のあとOPAMPのBufferで074などのOP AMP 1個とCA3080でVCF/VCAをまかなっています。VCFのantilogはARP typeのエミッタフォロワを温度補償に使ったシンプルな構成。 後期MOOG Tr. Ladderの標準として差動対とtr.負荷部分はCA3046を使用してマッチングを取っています。普通にそろえて部品代500円程度。ほぼMemory MOOGのVCF/VCAと同じ回路ですがMemory MOOGは resonanceの戻りもCA3080を使用してVCResonanceになっています。antilog 部分はARP風ではありません。ちなみにMemoryMOOGはVCOがCEM3340、EGがCEM3310です。1Voice分ぐらいはDIYしてみたくなります。
*: MS404のresonance VRの構成が少し特殊でこれはVRのカーブの補正かと思われます。(未確認ですが)
|
追記:2024/06/15
* A: SA13のladderはMS404の Ladderに較べて低域での発振振幅が極度に小さい件
* B: Ladder VCFはCVが小さい(Fcが低い)時の方が発振振幅が小さい件
LadderFilterについて調べていくとまず
* 1: Diode/Tr.ladderの違い
* 2: 最終の差動AMPの受けの違い
(抵抗DIRECT/Cap.t追加、差動AMPの前をBufferで受ける)
がありその組み合わせによっても特性が異なります。
おそらくFilter発振の特性に関してはWave KITのVCFのタイプが一番よくないVCFで上記MS404やTeisco等のTr. Ladderタイプで高インピーダンスのBufferをOPAMPの差動AMPの前に設置するものが部品は多いですがVCFとしての動作は一番シンプルにベストな特性になります、 たたladder VCFの場合はMS404の場合でも低域での発振が小さく高域になるにしたがって大きくなるのはそういう構造であってResonanceを上げた周波数特性を見てもピークが高域にいくほど強くなるので明らかです。

* tr. ladder VCFのCV変化に対するFcでのピークのレベルの変化
* ピークの強さはFcni対してLOG的な変化を示す。
* 発振まではいっていない時
上図で100Hzから8Khz程度で6dBほどのGAIN差があります。
(Teisoco 100F Tr. Ladder のVCF回路シュミ)40Hzからだと12dB
当初MS404はBufferされているのだから外部負荷(差動OPAMPの入力)の影響はなくかつresonance MAX時、正帰還の戻りのLadderの差動対の電流のピークはCVの値によらずテイル電流値ではりついているので正帰還ループを重ねれば同じになると考え、低域で発振振幅が落ちるのは後段のFilterのLossが低域で大きいのかと思っていました。
正帰還ループでの発振で制御電流が同じでもresonance VRを上げれ大きくなります。 これは当然帰還量が大きくなるからですがresonance VR位置が同じでも制御電流が大きいほうが発振振幅は大きくなり、
差動対での発生電流はCVにかかわらず同じ(resonance MAXではテイル電流の1/2まで到達する)だと考えていましたが、しかしよく考えればテイル電流値/2まで電流振幅が増大している状況では強力にLog圧縮がかかっている領域なのでCVの大小に関係なく同じ振幅レベルに達しているように見えても実は微小な差が生じているわけでかつ波形が変形している。resonance VRをMAXまで上げずVRが小さい状態でも発振している状況で見るとCVが大きい時の方がよりテイル電流値に近づいているのは明白で差動の電流特性のLog圧縮の本質を見逃してたことを実感。 上の方で書いたように差動対の電流の所でピークに達していても波形が違うので4LPFの最終出力ではCVが小さい方がSIN波の振幅が小さいことがわかりますのでそれが正帰還ループすれば明確な差が出るのでしょう。

* CVが低い場合と高い場合(Octave差)の発振過程の違い(resonance MAX時)
* 赤がそれぞれのCVni対するテイル電流値/2
* CV比1:2で制御電流比も1:2ですが上昇スピードは5倍程度違います。
特定周波数で安定して発振しているのだから正帰還ループで増幅と減衰のバランスがとれて平衡しているわけです。 たとえばresonance VR MAXで発振している時は差動対を流れる電流はクリップして矩形波に近くなりますが後段の1次LPFをと通ることにより丸くなっていき4段目の最終段においては振幅がかなり低下したSIN波になってこれを差動のOP AMPで増幅して低下分を補い正帰還ループでさらに発振振幅を増大させる。
増大するに従って差動の電流特性のカーブはゆるやかになるので結果GAINが下がってOut PUt電圧の増加は落ちある時点で平衡するわけで、CVが大きい時やresonance VRを上げた時の方が帰還の量は大きいのでカーブがなだらかになっても上昇できる余裕はまだあるということになります。 差動の電流特性としては電流が増大するに従ってLOG変化になり最後は変化なしなのでどんなに差動に印加される入力電圧が高くともテイル電流値の1/2以上にはなれません。結局CV値が小さい場合の方が積算による上昇率が小さいので上まで昇りきれないということでしょう。単位時間あたりの帰還の量。CVが小さい時は発振周波数が低いが高い時は大きいので周期差が意味を持つ、すなわち単位時間あたりの積算量が周波数が高い方が大きいので上昇スピードも速い、しそれが正帰還になっているのなら初めは指数的な変化になり上図とも対応しています。
と言うことでLadder VCFの発振においてはCVが小さいすなわちFcが小さくなるほど発振振幅は低下するのはさけられないので一定にしたければ正帰還のVCFのようにOUTPUTにDiode Limmiterをつけるようにしなければならないですがそのような処置をしたLadderVCFはありません。FcによってresonanceVRを電圧制御するのもよいかも知れません、
Ladderの負荷をOutputの差動AMPで受ける方法のバリエーション
WAVE KITのDiode Ladderの場合LadderVCF特有の特性に加えてさらに低域での発振振幅を下げる要素が存在します。WAVEKITのような受けだと差動のOP AMPの+側と-側の入力インピーダンスの違いによりladderの両側の電流振幅の片方の方が低下してしまい結果OPAMPのOUTPUT振幅の低下しかつこの傾向がCVの小さいFcが低いほど顕著になります。シミュレーションではCVが小さいと左右のLadderのdiode負荷では信号が逆相にならず同相になる場合があってこれだと後ろの差動AMPを通せば信号振幅がさらに減ってしまいます。
さらにWAVEKITのように差動OP AMPの前にCap.で直流Cutしていないとテイル電流にプラスしてOPAMP側に直流が流れこむのですがこれは低域で微分抵抗値が低い方にころぶので信号電流 *微分抵抗の電流電圧変換値は低下します。
FilterのCap.を外してGAINを見る。
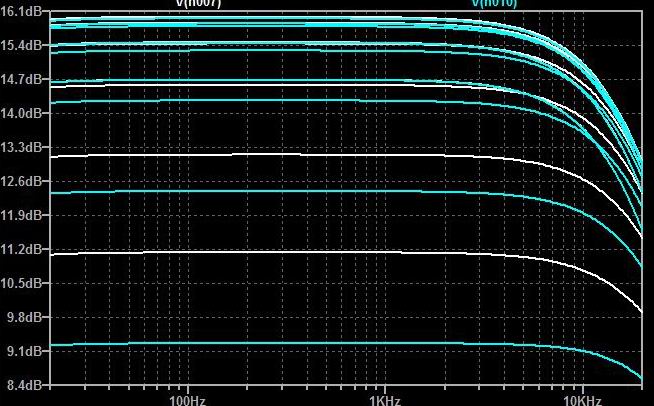
* 水: Cap.無し
* 白:Cap, 有り
*Cap.あり無しでのCVの大きさによる振幅の周波数特性(非filter動作時)
Cap,無しだとCV=1Vで0.8倍程度(-2dB)に減少
FilterのResonanceを上げGAINを見る。

* 水: Cap.無し
* 白:Cap, 有り
*Cap.あり無しでのCVの大きさによる振幅の周波数特性(filter動作時)
Cap,無しだとCV=1Vで0.8倍程度に減少
filter動作、非filter動作とも同量の低域でのGAIN減少となっている。

* Tr. LadderとDiodeLaddeの構成の違い
DiodeLadderは見た目とちがいとても複雑な構成になっております。これに対してTr. Ladderの方は4段が同一の電流入力typeのLPFであり最終段のTr.はfilterと負荷抵抗共用ですがdiodeは最終段の後に負荷用のdiodeが3段別についています。3個あるのはFcでのなでがた特性のためFcでの減衰が激しいので負荷の抵抗値を上げGAINを稼ぐためでしょう。さらにはdiode ladderは1段目のLPFは電流入力typeですのでCap.と並列になるRは図の赤枠の後段以降のCRになるのでしょう。
上の方でも書きましたがROLANDのSH3のVCFとWAVEKITのVCFは似た構成になっていますが2年後の後に出たSH5のDiode VCFはDiodeのかわりにTransistorのDiode接続を使っており、さらに同時期のSystem100も同様です。これはどのようなメリットがあるのか。DiodeよりTr.の方がばらつきが少ないともいわれていますが自分はそこまでの素子の知識がないのでわかりませんがメーカーがそのような対処をしているのでメリットがあってのことでしょう。さらに差動AMPをOPAMPを使わずSH5はCA3080、100はTransistorの差動AMPを使い+と-入力でインピーダンスが同じになるような対策、またCapacitorによって制御電流の影響の除去をしています。ROLANDとしては最後のDiode Ladder VCFのTB303のVCFはTr.のDiode接続で負荷はTr.Ladderと同じ方式です。
Tr. ladder VCFにおいて最終段のCR filterと負荷兼用のTransistorだけは差動対と同じようにMOOGの後期の機種ではDual Tr.が使われてることからその重要性が見てとれます。上記のTB303VCFもDiode ladderながらそれに準じており、Teiscoの100F以降の110Fなどは負荷Tr.のみならずLaddeを構成するTr.もみなDual Tr.構成です。これを機会に110F VCFを作ってみたいものです。
|
|
resonanceのVR位置と帰還量の関係
resonance VRをまわすと負帰還と正帰還が同時におきる。 出力の変化をさぐるべく VRのまわりに目盛り板をつけて角度に対する振幅を測定。 Fcを高めにセットし通過帯域の低めの周波数にSIN波を入れる。
1:負帰還
--------------
このVCFの場合、OP AMP OUTの電圧変化はVolumeの回転角に対してEXPOの下降で VR MAXで最低値となる。 反転入力のQ2のベースに入る電圧はこの時の値が最大値で OP AMP OUT = 反転入力電圧であり、この時だけ分圧はなし。 このためQ2のベースに印加される電圧は小さく最大100mV以下であり、これはOP AMP OUT電圧変化の逆特性の LOG変化であるとともに VR MAX以下ではresonance VRとR11の分圧になるため全体の電圧振幅は上記のように小さい。 WAVE KITのVCOの電圧振幅が5Vでそれが非反転入力には分圧されて100mVで印加されているのでそれと同等の電圧です。
上記のようにOP AMP OUTの電圧変化は EXPOなので resonanceを上げるに伴う音痩せ感は大きく、VRをAカーブにしてEXPOをLINEAR下降に近づけるようにした方がよいと思われる(*1)。
2:正帰還
--------------

* volume(100KB)の回転量と出力の反転入力ベースへの帰還量(分圧の度合い)
* (10で分圧無し(100%帰還))

* CV=12V時の VRの回連量と発振振幅の関係
17%の帰還量で最大発振振幅となる。発振振幅の変化は差動ペアの電流特性に酷似しているようだが。
CV値が異なってもカーブの形は似たような変化であるが発振開始位置(回転角)が後の方に移動する。
CV=2Vでも回転量60%を超えると発振、12Vにいたっては40%から開始してしまうのでとても使いにくい。せめて80%くらいからの発振になるようにしたい。 発振位置が早すぎるということではAカーブの方がよいのでしょう。
|
resonance VRをまわして得られるOP AMP 出力(正帰還分の発振要素)は VRが50%くらいまでは極少量で変化もEXPOであると思われる。(変化が小さくで観測不能) 出力が出始めは少しリニア気味の上昇だがその後の変化はLOG変化となり、VRがある程度いくとほとんど変化しない、すなわち収束する。 だからこの発振振幅は暴走することなく一定値を保てる。
一方 Q2のベースに印加される電圧は resonance VR MAXでは OP AMP OUTと同じ分圧されない値。 それ以下では VRとR11による分圧となる。 変化のカーブは初めEXPOであるがLOGカーブに変化してこれも収束する。
この場合のQ2のベースに印加される電圧は正帰還である為、出力が分圧されているにもかかわらず大きく OP AMP OUTが収束する前にいくにしたがって OP AMP OUT と変わらない電圧レベルになってしまうので MAX値が2Vあるとすれば中間でも1V以上はある。 いずれにしても resonance VR=MAXでは Fcが最高値の16KHzくらいでは 2V以上の電圧が直Q2のベースに印加されておりこれは上記の負帰還の信号レベルとはオーダーがだいぶちがう。
差動増幅回路の入力特性としてベースにどれだけ電圧を印加しても出力電流はテイル電流で決められた値以上にはなることはできない すなわち電流振幅がそれ以上は大きくなれないので電流波形がゆがんでクリップするのだが初めはハードクリップでなくソフトクリップである。
実際 、入力電圧(SIN波)が2V以上になった時のQ2のVbeの波形はSIN波の原型をとどめていないくらいLOG圧縮されている。 すなわち差動増幅回路の入力特性によって発振時の振幅増大という暴走はなく上記のようにLOGカーブで収束する。
|
*1:
MS404のVCFでは差動OP AMPのゲインが15倍とこのVCFよりもかなり小さいこともあってresonance Volを発振寸前の状態に持っていっても負帰還による振幅の減少は1/2以下になっている。 このことからも負帰還タイプのVCFではladder以降の差動AMPのゲインを大きくしないでも発振できることが望ましいように思い、ます。 SA13のVCFにおいてはオリジナルではゲイン200倍である為 resonanceを上げた時の振幅の減少がとても大きく実用的ではない。 ゲイン200倍と言うのはWAVEKITのVCFが低域で発振しないことへの対策なのでしょうが弊害が大きいです。
MS404のVCFは rogueのコピーですが resonanceのかけ方がオリジナルと異なりVRで分圧してベースに対してさらに直列に抵抗をかますタイプ。 さらに分圧の部分は擬似Cカーブになっているようですがこれがたいへん使いにくくVRが最後の方に行かないと効果が出ない。 MOOGのオリジナルはベースに直列にVRが入るタイプであり分圧はこのVRとベースの抵抗で行うタイプであるのでresonance Vol=0でもVRの値によっては厳密にはresonanceがわずかにかかってしまう構造です。 MS404の場合は50KΩなのでほとんど影響なし。 これを10Kにしてしまうとresonance=0でも少しピーキーになる。
rogueの回路図ではVRのカーブはAです。 上の方ではAカーブの方が変化が急にならなくて良いと書きましたが、ベースに直列にVRが入るタイプだとVR位置=0%で抵抗値最大、VR位置100%で0になるため、rogue VCFでAだと変化は下降のLOGとなるため、初め変化がなさすぎてVRの最後の方で急に効くという使いにくさになってしまう。 実際AカーブだとVRが60%の位置でresonanceが効き始め、発振も95%位置で突然発振という状況です。(ベースと並列にVRが入るタイプの場合は上記のようにAカーブがよい)

* 50KB使用時の回転量とMS404 VCF 反転入力ベース端子の電圧振幅

* 50KB使用時の回転量とMS404 VCF 負帰還出力振幅(90%以降は発振)

* 50KC使用時の回転量とMS404 VCF反転入力ベース端子の電圧振幅

* 50KC使用時の回転量とMS404 VCF 負帰還出力振幅(80%以降は発振)
50KCの方がスムーズだということがグラフからもわかると思います。 自分の404は rogueタイプの直列VRでかつ 50KのCカーブに修正してあり、よいresonanceのかかりになっていて発振寸前のふんばっている領域のコントロールがし易いです。 Cを使うのでなければ多少reso=0でピーキーですが20KBでもよいかと。
メーカーのシンセにおいてもresonanceのカーブはA,B,Cまちまちで使われています。 これは差動AMPのゲインなどのからみや負帰還とのからみで適正が変わってくるからなのではと思いますが.....
またこのrogueタイプの VCFでは発振時、反転入力のベースに印加される発振信号の電圧振幅は最大340mVとWAVEKITに比べて大変小さい値になっています。 総じてWAVE KITのVCFよりも安定していて使い易いという印象です。
|
|
|
その他.....
ladderからの出力の取り出し方としてこの抵抗負荷直結と言う方法は diode ladder filterでは普通に行われている方法ではありますがこのような問題をかかえているのでcapacitorの値を大きめにとりかつ制御電流もそれに見合った電流値にして問題が起きないようにしているのでしょう。 たまたま WAVE KITのVCFの capaciutorの値が小さかったので欠点が出てしまったということでしょうか。 オリジナルの回路ではそれを補うためRfの抵抗を10Mとしておりそれが使い難さとなっています。
|
調べて見るとladderからの信号を電圧で取る取り出し方にはいくつかのバリエーションがあります。
opamp buffer +差動AMP(instrumentation AMP風)
・ MOOG memory MOOG
・ MOOG Rogue (出力ampは+ OTA / resonance用は差動OP AMP)
・ Oberheim OBMX
・ Doepfer MS404(roufeと同様)
・ TEISCO 110F
OTAの使用
・ MOOG Taurus 1
・ MOOG sonic6
FET buffer +OTA
・MOOG polyMOOG
・MOOG microMOOG
・MOOG opus3
FET buffer +差動AMP
・TEISCO 100F
OTAを使うとAMPのゲイン指定に入力の抵抗を使わないで済むというメリットがあり(使ったとしても同じ値)、+/-入力での差ができないです。 上に上げたものは全てtransistor ladder VCFでありdiode ladderで電圧取り出しの物はないようです。 唯一 山下シンセの新版のdiode ladderにはinstrumentation AMP風の方法が明記されています。
|
SA13のladder VCFについては部品の定数をいろいろ変えたことによって一応 resonanceもそこそこ効くようにはなりました。 現状ではカップリングのCをつける対策まではして上記のような発振周波数下限22Hzで340mVまで出るようにはなりました。 それに伴いresonanceの波形もより変化が出るようになりました。
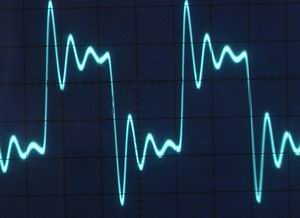
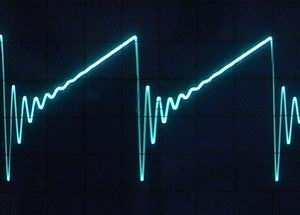
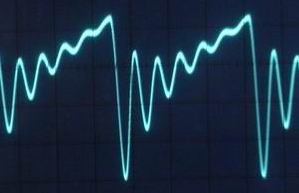
こうなってくると必ずしも負荷の取り出しをbufferを付けて電圧で取り出さなくとも実用上問題ないのではとも思うようになりました。 あとは低域での出力の低下をどれほど問題と見るかです。
実験して気づいたことはやはりFcでのゲイン低下、かなりのなで肩特性であるということです。 初め入力信号レベルが大きくてソフトクリップしたような少しなまった波形になっているのかと思いましたがこのなで肩特性のせいで波形がなまっているようです。 これはresonanceを少し上げてやることで改善されますので致命的ではありません。 むしろresonanceを上げると通過帯域のゲインが極端に下がるのはなんとかしたい物です。 肩特性がなで肩であることも悪いことではなく特性のバリエーションと見るべきでしょう。 K2000などもわざわざなで肩特性にするfilter parameterを持っていたりしますので。
ただ今回 transistor ladder (MS404)とこのdiode ladderを比較して見るとtransistor ladderの方がはるかに扱い易く感じました。 これを契機に昔作ったtransitor ladderの特性も調べてみようと思います。 また実験には主にROLANDの100MのVCO,VCFを使いましたが測定器的な使用には大変便利だと思いました。
部品定数等の変更箇所
R15 10K -- > 3.3K
filter capacitor 0.01uF --> 0.047uF
OP AMPのGAIN R3,R6 10M --> 4.5M
カップリングのCの追加 ---> 1uF
*:後日入手したマイコン誌の記事ではR3とR6は5Mに変更されていました。
まだ未処理
Frequency調整用POT
ladderからの出力取り出し --> bufferを付けて 電圧で取り出す
resonance VRを100K(B)から100k(A)に変えるか
DC balance用POTが必要かの検討
R9がなぜ 3.3Kか問題
Rf=4.5Mを小さくできないか
buffer付きでfilterのcを外してAMPのゲインを測定
高域で発振振幅が上がる理由をちゃんとわかりたい。
|
現実に使えるようにするには上記のようにいくつかのパーツや定数の調整が必要と言うことでこのVCFは初期状態の無改造ではちょと使えないVCF(*1)だったというおちです。 wavekitにはdiode ladder VCF単体のKITもありましたがそっちはどうだったのでしょう。 当時このVCFのKITを作った人は初期状態で満足していたのでしょうかと一瞬思いました。 万能基板を含めた部品代もせいぜい500円から600円くらいですが、このVCFはこれだけ楽しめて勉強になるいい題材だと思いました。
発振状態等がだいぶよくなったので OP AMPのRfを4.5Mでなく1.5M少なくとも3Mくらいに落としても大丈夫かも知れません。 実際diode ladderでRf=1.5Mという値のsynthも多いですし。 実験に使った万能基板は色々部品を取替えしたので裏のはんだ面が結構荒れてしまいました。 実用機として使うには再度作りなおしが必要というか、出力を電圧で取り出す実験をするにも基板を追加するしかないですが、どうせ作るなら次は他のladde VCFに挑戦してみたいとも思います。 それ以前にちゃんとした音出しはまだなのでDC OFFSETによるクリック音がどの程度気になるか等の検討もまだです。
*1:
と言いつつも回路自体は1974年当時のSH-3のVCFととてもよく似ています、 やはりcapacitorの定数の違いが大きいのでしょう。 ちなみにSH-3のfilterのCは0.068uF、Rf=1.5M、テイル電流用の抵抗は3.3Kです。
SH-3と言えば当時の噂としてSH-3はMOOG方式のtransistor ladderを使っていたので特許の関係で後にdiode ladder VCFにチェンジしたSH-3Aが発売されたと言われていましたが実際は、SH-3がdiode ladder、 SH-3Aが transistor ladderです。 SH-3Aの方はしっかりcapacitorでカップリングをしています。
capacitorあり
ROLAND SH-1000(1973) (filterのC=0.068u)
ROLAND SYSTEM100(1975) (filterのC=0.068u) *2:
ROLAND SH-5(1975) (filterのC=0.068u) *2:
ROLAND TB-303(1982) (filterのC=0.033u) *2:
Firstman SQ01(197?) (filterのC=0.1u)
*2: transistorのdiode接続
capacitor無し
EMS VCS3(1969) (filterのC=0.1u)
EMS AKS(1972) (filterのC=0.1u)
ROLAND SH-3(1974) (filterのC=0.068u 制御電流用のR=3.3K)
JEN: SX2000(1978) (filterのC=0.1u)
DIY synth
PE: Minisonic(1974) (filterのC=0.047u)
PE: Minisonic2(1976) (filterのC=0.047u)
電子展望(1976) (filterのC=0.068u 制御電流用のR=3.3K)
初歩のラジオ(1977) ( filterのC=0.068u)
トランジスタ技術 (1977) ( filterのC=0.22u 制御電流用のR=4.7K)
初ラ別冊 エフェクター入門(1982) ( filterのC=0.68u) <--おそらくミスプリか
そもそもメーカ製synthでは思ったほどdiode ladder VCFは多くなく、DIY synthにdiode ladderが多いということです。 理由としてOTAが出現すると激減したということでしょうか。 DIY記事ではMOOG transistor ladderは特許の関係もあり使いにくかったのか。 調べたついでにfilterを構成するのcapacitorの値も上に明記しておきます。(カップリングのCではありません) DIY synthでは カップリングのCを付けているものはありませんでした。
ちなみに、初ラ別冊 エフェクター入門のVCFのladderからの信号の取り出し方が SYSTEM100のそれと同一でした。 当時は回路図などは今のように流通していなかったはずですが、持っている人は待っていたのでしょう。 さらに気づいたことは多くのdiode ladder VCFはfilterが4段構成でなく5段構成になっており初段のfilterはFcを他の4段より高くとってFc付近でのなで肩を改善しているようです?。 あとdiode ladderとはちょっとばかり違いますが、スタイナーVCFやKORGのdiode ringも差動回路がらみでにたような原理を使ったfilterでした。 一見違うような回路に見えますが実はdiode ringの動作はdiode ladderの動作によく似ています。
|
<2024/06/15 rev0.2>
<2017/07/20 rev0.1>
<2016/10/30 rev0>
|

|