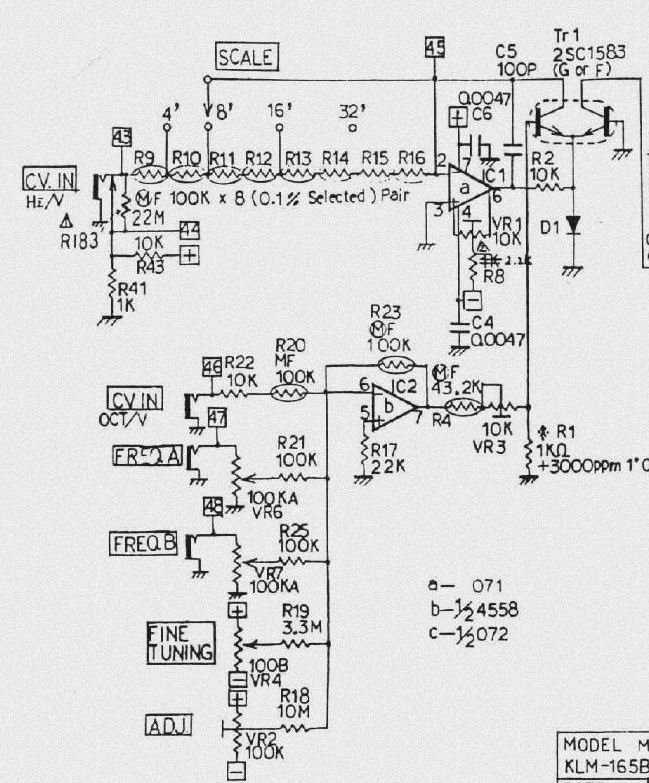
KORG Hz/V Oct/V 嫟梡 antilog AMP
MS僔儕乕僘偺VCO偼婎杮 Hz/V 側偺偱偡偑Oct/V偵傕懳墳偟偨儐僯乕僋側VCO偵側偭偰偍傝丄捠忢偺 Oct/V synth偲摨條側 antilog amp傪搵嵹偟偰偄傑偡丅丂偙偙偱偼偦偺antilog amp偵偮偄偰峫偊偰傒傑偡丅
antilog AMP偺昁梫惈偼偙偙傪嶲徠偺偙偲丅
師偵昗弨揑側antilog AMP夞楬偺婎杮摦嶌傪峫偊偰傒傑偟傚偆丅
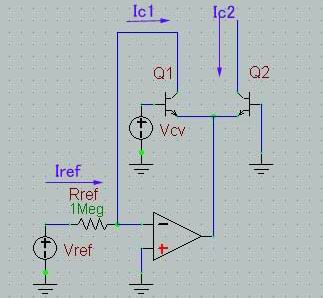
* 幚嵺偺夞楬偱偼僄儈僢僞偲OP OUT偺娫偵曐岇掞峈
丂OPAMP偺(-)抂巕偲(OUT乯娫偵敪怳巭傔Cap.偑擖傞
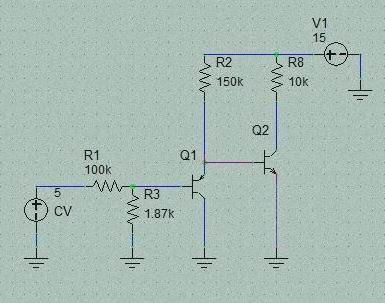
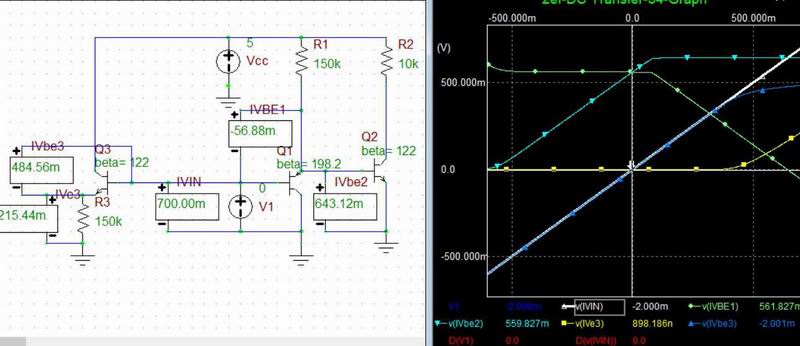
慜採偲偟偰丄壒奒傪嶌傞偨傔偺婎杮夞楬偼Q2偺 Tr. 1愇偵傛傞Vbe偲Ic偺娭學偲偄偆transistor偺婎杮惈幙傪棙梡偟偨夞楬偱偡丅丂巆傝偺 Tr.偲 OP AMP偼婎杮OFFSET壏搙曗彏梡偱偡丅乮恾偺夞楬偱偼 SCALE曗彏偼柍偟乯
丂俬c=俬s{倕倶倫(q*倁be/kT)-1}
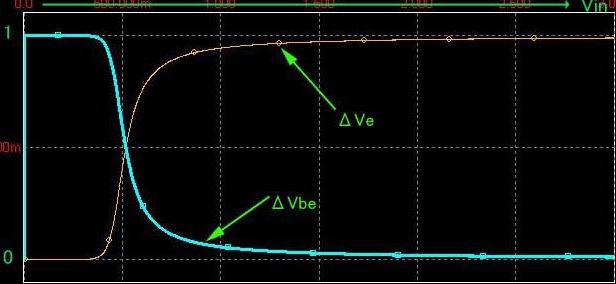
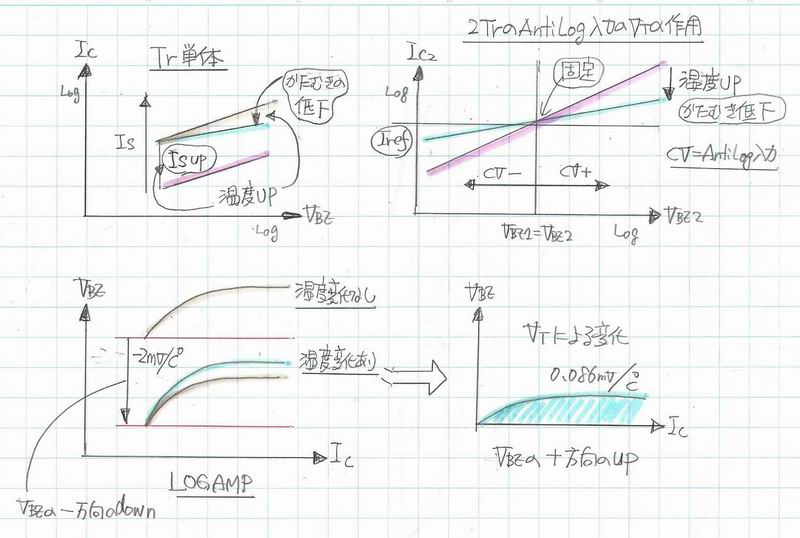
忋幃偱OFFSET曄摦偵偐偐傢傞偺偑Is 偱偡丅丂Is偼夞楬摦嶌偲偟偰偼昞偵弌偰偙側偄梫慺側偺偱Ic偲Vbe偺娭學偵偍偄偰偼偙偺幃偼壏搙曄壔偵懳偟偰Ic傪屌掕偟偰偍偗偽Vbe偑曄壔偟Vbe傪屌掕偡傟偽Ic偑曄壔偡傞偙偲傪帵偟偰偄傑偡丅
夞楬揑偵I們傪屌掕偟偰偍偔偲Vbe偼壏搙偑1搙憹壛偡傞偲栺2mV掅壓偟傑偡丅丂Vbe傪屌掕偟偰偍偔偲Ic偼 1搙偺憹壛偱栺8亾憹壛偡傞丅丂偙偙偱廳梫側偺偼Vbe偼柧敀側悢抣側偺偵懳偟偰Ic偼妱崌偵側偭偰偄傑偡丅丂偙傟偼摦嶌揰偵傛偭偰Ic偺曄壔検偑堎側傞偨傔偱偡丅
Q1偺C-E娫偼OP AMP偺FB loop偵擖偭偰偄傞偺偱Ic偺抣偼嫮惂揑偵婎弨揹棳Iref偲摨偠抣偵側傝丄(*0)偙傟偼壏搙偑曄壔偟偰傕堦掕抣傪曐偪曄壔偟傑偣傫丅丂傛偭偰Q1偺Vbe偼儀乕僗偵報壛偝傟傞揹埑CV偺曄壔偵懳偟偰曄摦偟傑偣傫偺偱 CV偺曄壔偼 Q1傪宱桼偟偰娫愙揑偵Q2偺B-E娫偵慡偰揱傢傝傑偡丅(*1)丂CV偑戝偒偔側傟偽Q2偺Vbe2偼媡偵掅壓偟傑偡偺偱捠忢偙偺宍幃偺 antilog AMP偱偼CV偼OP AMP偺斀揮憹暆夞楬傪宱桼偟偰Q1偵報壛偝傟傑偡丅
*0: OPAMP偵傛偭偰Iref偼掕揹棳尮偵側偭偰偄傞丅
*1: Vin - Vbe1(屌掕抣)偑僄儈僢僞偵揱傢傞偺堄丅
壏搙曄壔偵懳偟偰 Is偑曄摦偟傑偡偑 Ic1偼屌掕偝傟偰偍傝丄 Vbe1偼屌掕偝傟偰偄側偄偺偱忋婰偺傛偆偵壏搙偑忋偑傟偽Vbe1偼掅壓偟偰忋幃傪枮偨偡傛偆偵乮Ic屌掕)曄壔偟傑偡丅丂CV屌掕側偺偱Q1偺僄儈僢僞揹埵偑忋徃偡傞偙偲偵側傝僄儈僢僞偼 Q2偲嫟捠側偺偱Vbe1偺曄壔偑偦偺傑傑Q2偺Vbe2偺曄壔偲側傝傑偡丅丂偡側傢偪Ic1傪屌掕偟偰偍偔偙偲偱壏搙曄壔偵懳偟偰Ic2傕摨條偵曄摦偟側偄偙偲偵側傝傑偡丅(掕揹棳尮偺晄巚媍傪棙梡偟偨摦嶌偲偄偆偐丅)
壏搙曄壔偵懳偟偰LOG僗働乕儖忋偺Ic-Vbe嬋慄偼扨偵X幉偵懳偟偰嵍塃偵摦偔偙偲偱偡偐傜丄偙偺Ic偑曄摦偟側偄偲偄偆偙偲偼側偵傕偟側偄応崌偺壏搙忋徃偵懳墳偟偨 Ic-Vbe嬋慄傪 壏搙曄壔埲慜偺Ic-Vbe嬋慄偵岦偗偰壏搙曄壔帪偺儮Vbe暘X幉偵懳偟偰嵍偵堏摦偟偨偙偲偲摍壙偱偡丅
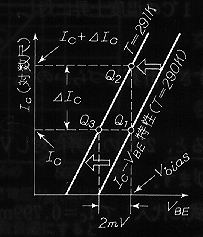
* OFFSET曗彏偺僌儔僼
偡側傢偪CV偺曄壔偼Q1偺Vbe1偵偼塭嬁偣偢丄Q2偺Vbe2偺曄壔偲側傝摦嶌揰偑堏摦偟傑偡偑丄壏搙曄壔偵懳偟偰偼Q1偺Vbe1偺曄壔偑 Q2偺Vbe2偵傕塭嬁傪梌偊傞丅丂Q1偺Vbe偼壏搙僙儞僒乕偲Vbe2偺OFFSET挷惍偡傞曗彏夞楬偱傕偁傞丅丂antilog揹棳尮懁偺僩儔儞僕僗僞偼壏搙曗彏懁偺僩儔儞僕僗僞偺 壏搙摿惈傪宲彸偡傞偲偄偆偙偲偱偡丅
|
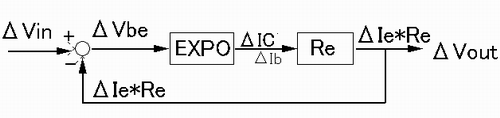
Ic1傪屌掕偟偰偄傞偺偱Vcv偑曄壔偟偰傕Vbe1偑曄摦偣偢丄antilog摿惈梡偺Tr.丂Q2偵報壛揹埑偑娫愙揑偵揱傢傞丅Ic傪屌掕偟偰偄偰傕壏搙曄壔偵懳偟偰偼EXPO偺幃傪枮偨偡傛偆偵Vbe偑曄壔偡傞丅丂偙偺晹暘偑巒傔偼傢偐傝偵偔偄偐傕抦傟傑偣傫丅
側偍CV IN偼OFFSET曗彏梡偺Tr.偵報壛偡傞偺偱偼側偔antilog梡Tr.偺B-E娫偵捈愙報壛偟偰傕摨偠偱偡丅乮壓恾乯 偙偺応崌Ve偼屌掕側偺偱Vcv偺曄壔偱Vb2偑捛廬偟傑偡丅
偙偺応崌偼CV擖椡偺斀揮OPAMP偼晄昁梫偵側傞偺偱passive CV mixer偱偄偄応崌偵偼桳岠偐偲丅 尨棟愢柧揑偵偼偙偪傜偺曽偑傢偐傝傗偡偄偐傕抦傟傑偣傫丅CV mixer偵active mixer乮OPAMP乯傪巊梡偡傞応崌偼巒傔偵帵偟偨夞楬偵側傝傑偡偺偱晛捠偼偦傟偵側傝傑偡丅梫偼偳偪傜偺Tr.偺儀乕僗偵怣崋傪擖傟偰傕antilog amp偲偟偰摦嶌偡傞傢偗偱偡偑Q1懁偐傜擖傟傞偲媡憡偵側傞揰偲Q侾懁偐傜擖傟偨CV偼嫟捠僄儈僢僞偵偦偺傑傑偔傢傢傞偺偱僄儈僢僞揹埵傪忋偘偰偟傑偆偺偱Q1偺Vbe偼壓偑傞偲尵偆揰丄Q俀懁偐傜擖傟傟偽Q2偺Ve偼忋偑傞
|
幃揑偵偼丄
CV 0V偺帪 Q1偲 Q2偼摿惈偑偦傠偭偰偄傞偲偄偆慜採側偺偱椉C-E娫傪棳傟傞揹棳偼 摨偠偱 Iref偩偗棳傟傑偡丅(丂 Cv=0V帪丂exp(0)=1側偺偱 Iref=Isat=Ic2丂)
偙傟偑OFFSET曗彏偱偡偑丄Isat偵曄傢偭偰Iref傪掕媊偟偰EXP娭悢偺怴偨側弶婜抣(奐巒億僀儞僩)傪掕媊偡傞偙偲偱傕偁傝傑偡丅
忋婰偺夞楬乮堦斣巒傔偺夞楬乯偵偍偄偰
丂* Iref=Isat*exp(Vbe1/Vt)
丂* Ic2=Isat*exp(Vbe2/Vt)
丂* Vcv=Vbe2-Vbe1
傛偭偰
丂* Ic2/Iref=exp((Vbe2-Vbe1)/Vt)
備偊偵 Ic2偲Vcv偺娭學偼丄
丂*Ic2=Iref*exp(Vcv/Vt)
偲側傝Isat偑徚嫀偝傟傑偟偨丅丂Isat偼幃偺憖嶌忋柍偔側偭偨偺偱偙偺夞楬 偼Isat偺塭嬁偑僉儍儞僙儖偝傟偨偺偱偟傚偆偐丠丅丂Isat偵偲偭偰曄傢偭偨Iref 偑壏搙偵塭嬁偝傟側偗傟偽偙偺夞楬偼 OFFset堏摦偑僉儍儞僙儖偝傟傞偲偄偆 偙偲偵側傞偺偱偡偑丅丂幚嵺Iref偼忋偺夞楬偵偍偄偰壏搙偺塭嬁傪婎杮揑偵偼庴偗側偄偺偱Q2偺(*)OFFset堏摦偑僉儍儞僙儖偝傟傞偲偄偆偙偲偵側傝傑偡丅( Rref偼嬥懏旂枌掞峈傪巊偆偙偲偑慜採乯
Vbe偑Vcv偵抲偒姺傢偭偰偄傞傢偗偱偡偐傜丄僩儔儞僕僗僞偺Vbe偑0偐傜巒傑傞 偲偄偆偙偲偱偼側偔偡偱偵Ic1偺暘偩偗Vbe偼僶僀傾僗偝傟偰偄傞傢偗偱偡偑丄 偙偺帪揰傪怴偨側奐巒揰偲偡傞側傜偽Vbe2偺偐傢傝偵Vcv丄Isat偺戙傢傝偵 Iref偱偍偒偐偊傞偙偲偑偱偒丄Vcv偺曄壔偱Ic2偑曄壔偟偰偄傞偙偲偵側傞 偲偄偆偙偲偱偡丅
Ic = Iref * Exp(Vcv / Vt)
丂iref 100uA Vt=26mV偲偡傞偲
丂Vcv偑18mv偱 Ic = 100uA * EXP(18m/26m) =200uA
丂Vcv偑2攞偺36mv偱 Ic = 100uA * EXP(36m/26m) =400uA
Vbe = Vt *Ln (Ic/Iref)
丂Iref=100uA , Ic=200uA偲偡傞偲 Vbe = 26mV * Ln(200uA/100uA) =
丂26mv* 0.7=18mV
丂Iref=100uA , Ic=400uA偲偡傞偲 Vbe = 26mV * Ln(400uA/100uA) =
丂 26mv* 1.4= 36mV
偲偄偭偨嬶崌
偙偺夞楬偺億僀儞僩偼Ic傪偳偆傗偭偰屌掕偡傞偐偲偄偆晹暘偲 偳偆傗偭偰Vbe傪娫愙揑偵梌偊傞偐偲偄偆揰偱偡丅丂偡側傢偪報壛揹埑屌掕忬懺 偱偁偭偰傕丂壏搙曄壔偵懳偟偰Ic傪屌掕偟偨忬懺偱Vbe偑曄壔偱偒傞夞楬偱偁傞偲偄偆 偙偲丅丂偝傜偵報壛揹埑偺曄壔偵懳偟偰偼antilog摦嶌傪偡傞僩儔儞僕僗僞偵偼偪傖傫 偲報壛揹埑偑揱払偱偒傞夞楬偩偲偄偆偙偲偱偡丅
* 梋択
丂偳偆偟偰忋婰夞楬偱偼Tr. 傪棳傟傞Ic偼壏搙偱曄摦偟側偄偺偐丠
* SCALE曗彏
埲忋偑antilog偺OFFset曗彏偱偡偑壏搙曗彏偵偼傕偆堦偮octave偺Span傪曗彏偡傞昁梫 丄偡側傢偪EXPO僇乕僽偑壏搙偵塭嬁偝傟側偄傛偆俿偺梫慺傪庢傝彍偔昁梫偑偁傝傑偡丅丂 壏搙偑憹壛偡傟偽 EXPO嬋慄偺孹偒偑掅壓偟傑偡丅丂堦斒揑偵偼 +3300ppm偺tempco掞峈傪antilog偺暘埑夞楬偵梡偄偰壏搙偑忋徃偡傟偽暘埑斾偑憹壛偡傞傛偆偵偟偰T偺塭嬁傪僉儍儞僙儖偟傑偡丅
捠忢偙偺夞楬偼忢壏(T=300K)嬤曈偱巊梡偡傞偺偱1/T偺崁偼偍偍傛偦1/300偲側傝傑偡丅丂 傛偭偰 壏搙偑1搙曄壔偡傞偲1/300亷偺曄壔偲側傝傑偡丅丂偙傟傪曗彏偡傞偨傔偵偼 Vin傕1/300亷偱曄壔偡傞傛偆偵偡傟偽傛偄偺偱偦偺堊偺傂偲偮偺曽朄偲偟偰偼 R1偲R2偱掞峈暘埑傪嶌傝GND懁偺R2偑壏搙 曄壔偵懳偟偰+1/300亷偺妱崌偱掞峈抣偑儕僯傾偵憹壛偡傞傛偆偵偡傟偽傛偄偙偲偵側傝傑偡丄...偡側傢偪丂1 / 300亷 = 0.33%/亷
R2偵惓偺壏搙學悢(+0.33%/亷) 暿昞尰偱偼+3300ppm傪帩偮tempco 掞峈傪梡偄傞偙偲偱丄壏搙偑忋壓 偡傟偽報壛偝傟傞揹埑傕忋壓偡傞傛偆偵偟偰寢壥丄壏搙埶懚傪僉儍儞僙儖偡傞傛偆偵偟傑偡丅
tempco 掞峈偼忢壏(T=300亱K)偺帪偵掞峈抣100亾偵側傞傛偆偵嶌傜傟偰偄傞偲巚傢傟傞偺偱報壛偡傞惂屼揹埑偺尭悐斾偼忋婰偺傛偆偵T=300亱K偺帪偺kT/q偺抣26mV偐傜 1V偵懳偟偰26mV*ln(2)=18mV偵側傞傛偆偵愝掕偟偰偍偗偽傛偄偙偲偵側傝傑偡丅
傾僢僥僱乕僞偲偟偰R1/(0.0033*(T-300)*R2)+R2偺宍偲側傞偨傔 R1偲R2偺斾偑嬤偄抣偱偁傟偽壏搙曄壔偵敽偆尭悐斾偼儕僯傾偵忋徃偣偢懳悢僇乕僽揑忋徃偵側傝傑偡偑偙偺応崌R偲R2偺斾偼50攞掱搙偁傝傑偡偺偱幚幙儕僯傾側忋徃偲傒側偣傑偡丅
MS20偺antilog偺scale曗彏偼摿偵偝傟偰偄偢摨幉働乕僽儖偺愭抂曐岇梡偺價僯乕儖Cap傪Dual Tr.偵偐傇偣偰偁傞掱搙廃埻偺壏搙偲Dual Tr.傪幷抐偡傞偙偲偱壏搙曄壔傪彮側偔偡傞偲偄偆岺晇偑偝傟偰偄傑偡丅丂MS20偼偁偔傑偱 Hz/V偑儊僀儞偺VCO偩偐傜偱偡偑摨偠MS僔儕乕僘偱傕姰慡 Module type偺MS50偺VCO偼Tempco掞峈偱scale曗彏傪偟偰偍傝偙傟偼姰慡偵Oct/V丄Hz/V椉搧巊偄偺VCO偲側傝傑偡丅
T偺塭嬁偵傛傞scale曗彏傪偟偰偄側偄忬懺偱偼EXPO僇乕僽偺孹偒偑壏搙偺忋徃偵懳偟偰掅壓偡傞偺偱Ic屌掕帪偺嚈Vbe偺曄摦暆偑堎側傝摦嶌揰偑崅偄偲彫偝偔側傝offset曗彏偺Tr.偲 antilog 偺 Tr,偼摦嶌揰偑捠忢堎側傞偺偱scale曗彏側偟偩偲 offset曗彏偑antilog Tr.偺摦嶌揰偵傛偭偰曄壔偟偰偟傑偆偙偲偵側傝寢壥揑偵偼offset曗彏偵傕塭嬁偑偁傞丅偙傟偼幃拞偵2偭偺壏搙偵懳偟偰塭嬁偡傞僷儔儊乕僞偑偁傞偙偲偐傜傫傕摉慠偱偡偑丅傛偭偰娙堈antilog埲奜偼丂offset/scale曗彏偺椉曽偑昁梫側偺偱偟傚偆丅
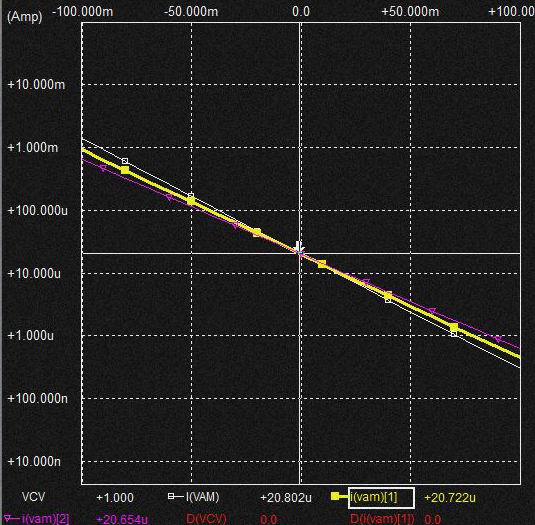
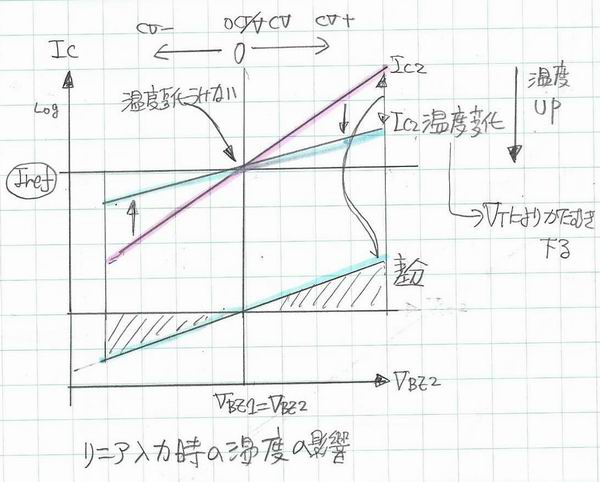
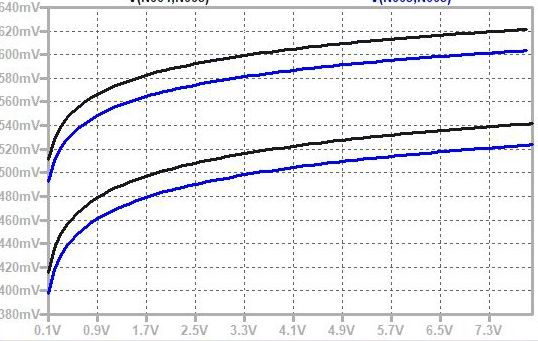
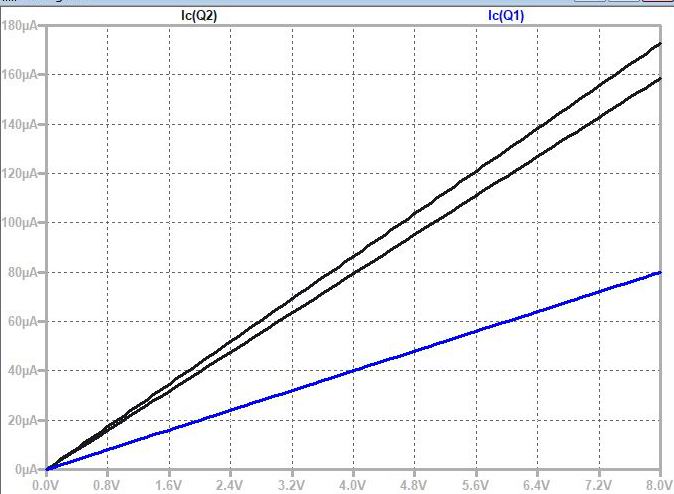
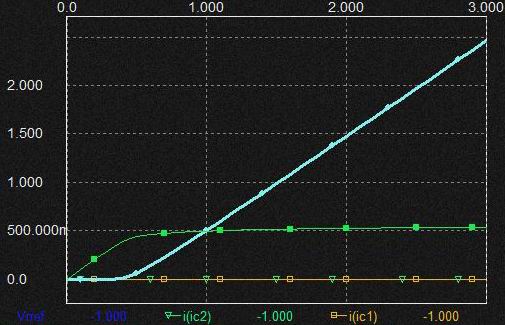
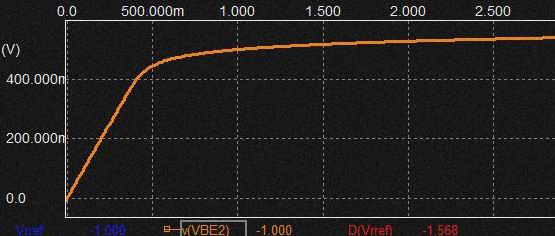
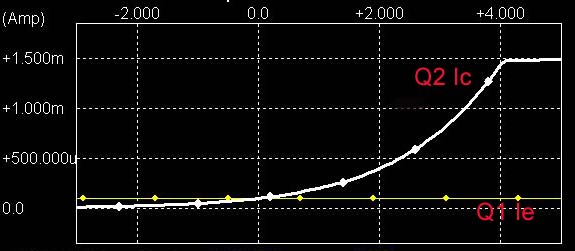
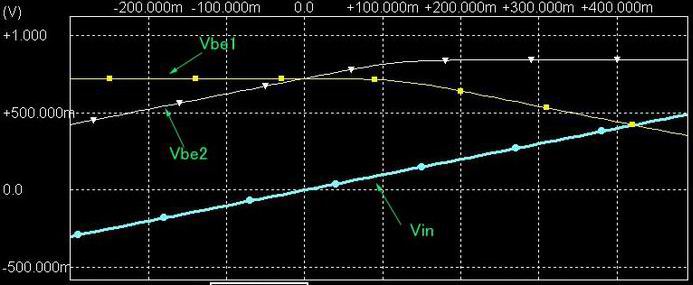
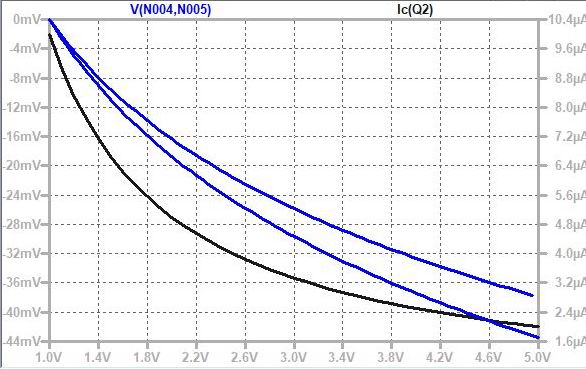
* 奺怓:CV壜曄帪偺壏搙偺堘偄偵傛傞Ic偺曄壔(Y幉LOG僗働乕儖)
CV=0V帪偡側傢偪 椉僩儔儞僕僗僞偺摦嶌揰偑摨偠側偺偱offset曗彏偑偱偒偰偄偰傕scale曗彏偑側偄偲 寢壥揑偵偼椉幰偺摦嶌揰偑曄傢傞偲壏搙偺塭嬁偱Offset偑偢傟傞偺恾丅
幚嵺忋偺巊梡柺偱峫偊偰傕OFFSET曗彏偺岆嵎傪媧廂偡傞偵偼Tune 偮傑傒傪壜曄偡傟偽偡傓偺偱岆嵎偺斖埻埲忋偺tune愝掕傪VR偵愝偗傟偽傛偄偱偡偑scale曗彏偑偝傟偰偄側偗傟偽壒奒偵懳墳偝偣傞偨傔偵偼偦偺偮偳攞棪傪峀斖埻偵傢偨偭偰挷惍偡傞昁梫偑惗偠偰偟傑偄戝曄偱偡丅
|
忋婰Dual Tr.偺廃曈壏搙偺屌掕傪揙掙偟偨偺偑uA726傗SSM2100摍偺峆壏憘偵傛傞峆壏曗彏偱偡丅丂僨傿僗僋儕乕僩偱偼 MOOG偺彫宆synth偺悢婡庬偑Tr. Array傪巊偭偨峆壏憘傪棙梡偟偰偄傑偟偨丅
偁偲摉帪偺媄弍偲偟偰偼CPU傪巊偭偨auto tune丄偙傟偵偼抦傞尷傝偱偼2偭偺僞僀僾偑偁傝傑偡偑偳傜傕棟憐抣偲尰嵼偺antilog Tr.偺嵎傪杽傔偰曗惓偡傞曽朄偱婎杮偼FeedBack惂屼偱偡丅丂偝傜偵偼CEM3340偺+3300ppm偺壏搙學悢傪帩偮忔嶼婍傪梡偄偰忋婰偺暘埑掞峈偺偐傢傝偵偮偐偆摍偺曽朄偑偁傝傑偟偨丅偁偲偼僒乕儈僗僞乕傪暘埑掞峈偺媡偺曽偵庢傝晅偗傞曽朄偱VCF偺antilog偵偼傛偔巊傢傟偰偄傑偟偨丅 忋婰偺曽朄偼擬揹埑Vt偺曄壔傪専弌偟偦傟傪尦偵忔嶼傪偟偰壏搙T偺塭嬁傪僉儍儞僙儖偡傞曽朄偱偡偑忔嶼婍梫慺偑暿偵昁梫偵側傝傑偡丅梫偼Tr.偺2偭偺摦嶌揰偐傜壏搙曄壔偵懳偡傞Ic嬋慄偺孹偒傪専弌偟偰偦偺寢壥偐傜V倲梫慺傪庢傝弌偡曽朄丅暿偺曽朄偲偟偰偼antilog Amp偺儕僯傾擖椡偵CV傪壛偊偝傜偵Oct/V擖椡偵CV傪壛偊偨帪antilog偺揹棳弌椡偼儕僯傾側弌椡偵側傞偲偲傕偵憹壛偺孹偒偑Vt偵斾椺偡傞偲偄偆尰徾傪棙梡偡傞曽朄傗OTA偺GAIN偑惓偺壏搙學悢傪帩偮偲偄偆偺傪棙梡偡傞曽朄摍丅
|
|
* antilog amp偺丂Tr.偺儀乕僗偵偮偗傞暘埑掞峈偵偮偄偰
偨偲偊偽 10K : 180 杮棃B-E娫偵捈愙揹埑傪報壛偟側偄偲Vbe-Ic摿惈偼 EXPO偵側傜側偄丄掞峈偑擖傟偽晧婣娨偑惗偠偰報壛揹埑偼丂LOG偵側傝弌椡揹棳偼捈慄偵側偭偰偟傑偆傛偆偵傕巚傢傟傞偑丅 掞峈暘埑偟偰偄傞偺偱丂CV擖椡偵懳偟偰儀乕僗偵報壛偝傟傞揹埑偼丂1/50掱搙偵側傞偺偱 CV傪 1偐傜10V梌偊偨偲偟偰傕 180mV掱搙偟偐壜曄偝傟側偄丅 Initial CV傪偁偨偊側偗傟偽偙偺掱搙偟偐儀乕僗偵偼報壛偝傟側偄偺偩偐傜 Tr.偺B-E娫 掞峈 rb偼偲偰傕戝偒偄抣偱偟偐側偄丅丂幚嵺偙偺掱搙偺揹埑偱偼Ic偼戝曄彫偝偔丂nA僆乕僟乕偵側偭偰偟傑偆偺偱initial揹埑傪梌偊傞偺偩偑丅 rb = { (Kt/q) /Ic } *hfe
hfe傪100偲偟偰傕 Ic=100u偱 300K偔傜偄偱偁傞偺偵懳偟偰丂暘埑掞峈傪暲楍偵偟偨抣偼戝偒偔偰傕600兌掱搙偱偁傞偺偱傎傏捈愙揹埑傪 儀乕僗偵報壛偟偨傕偺偲摨偠偙偲偵側傞丅 偡側傢偪antilog amp偺Ic偺摦嶌斖埻偑悢uA偐傜悢昐uA側偺偱偁傞丅丂Ic偑憹偊傟偽摉慠報壛揹埑偼B-E娫偵偼偐偐傜側偔側偭偰偄偔偑丅丂偙傟偑杮棃僟僀儗僋僩偵梌偊傞傋偒偲偙傠傪掞峈暘埑偟偰傛偄棟桼丅 |
MS偺 antilog夞楬
MS偵偍偄偰偼捠忢屌掕偱巊梡偡傞Iref懁偺揹埑尮偵懳偟偰壒奒偺摍斾楍偺CV傪敪惗偝偣傞 KEY CV夞楬傪抲偒偝傜偵Rref偵摉偨傞掞峈晹暘傪OCTAVE愗傝懼偊偵棙梡偟偙偙偱KEY CV偵懳偟偰忔彍嶼傪峴偭偰偄傑偡丅
* MS20偺Key CV弌椡偼嵟掅Key偺C偐傜嵟崅ey偺C傑偱octave偛偲偵1/2/4/8V傪弌椡丅
KEY CV擖椡懁傪Hz/V擖椡(儕僯傾擖椡)偲偟偰偄傑偡丅丂偙傟偼
丂*Ic2=Iref*exp(Vcv/Vt)
忋婰偺幃偺Iref偵奩摉偡傞偐傜偱偙偺晹暘偼 EXPO娭悢偺塭嬁傪庴偗側偄偐傜Hz/V擖椡 偲尵偆偙偲偵側傝傑偡丅
幃忋偱偼儕僯傾側曄壔側偺偱偡偑夞楬偲偟偰杮摉偵儕僯傾側曄壔側偺偱偟傚偆偐丅丂Iref偲Ic1偼摨偠抣偵側傞偺偱Iref偺曄壔偑儕僯傾偱偁傟偽(*1)丂Vbe1偺曄壔偼 LOG曄壔偲側傝偦傟偑Q2偺B-E娫偵揱傢傞偺偱Vbe2傕LOG曄壔丄偦傟偑 EXPO曄姺偝傟傞偺偱 Ic2傕儕僯傾側曄壔偲側傞丅
*1:
Ic1偺曄壔偱嫮惂揑偵Vbe1偑Vbe偲Ic偺娭學偑 EXPO偱偁傞偙偲傪枮懌偡傞傛偆偵曄壔偡傞偺偱Ic1偺曄壔偑儕僯傾偱偁傟偽Vbe偺曄壔偼 LOG丅
傛傝扨弮偵偼 OP AMP偲FB儖乕僾撪偺NPN Tr.偱峔惉偝傟傞夞楬偼儀乕僗揹埵屌掕帪丄LIN. CV擖椡偵懳偟偰偼log amp偵側傞偲偄偆偙偲偱偡丅丂傛偭偰 antilog amp慡懱偲偟偰偼Log曄壔偺揹埑偑傕偆堦曽偺Tr.偺B-E娫偵報壛偝傟傟偽Ic偼儕僯傾偵側傞偲偄偆偩偗偱偡丅
MS20偺Hz/V擖椡偵懳偟偰偼捠忢丄壒奒偺摍斾楍偵懳墳偟偨Key CV偑擖椡偝傟丄偦傟偑Iref偵曄姺偝傟傑偡丅OP AMP偺 FB loop偵傛偭偰嫮惂揑偵偦傟偲摨偠抣偺Ic1偑敪惗偡傞偲摨帪偵Ic1偑LOG曄姺偝傟偨Vbe1偑敪惗偟傑偡丅丂偙偺嵺Ic1偑Octave曄壔偁傞偲偡傞偲Vbe1偺曄壔偼18mv丄Ic1偺曄壔偑敿壒暘偩偲偡傞偲Vbe1偼1.5mV偲Vbe1偺曄壔偼儕僯傾側曄壔偲側傝傑偡丅
Vbe1偺曄壔偼忋弎偲摨條偵Q2偺Vbe2偵摨検偱揱払偝傟丄Q2偺EXPO曄姺偱Ic2偑敪惗偟傑偡丅丂CV=0V帪偼Ic1偺曄壔=Ic2偵側傝Ic1偺曄壔偑僐僺乕偝傟偨宍偵側傝Hz/V偺揹埑擖椡偼儕僯傾偵Ic2偵曄姺偝傟傑偡丅 偡側傢偪儕僯傾擖椡偺揹埑曄壔偑antilog out偺揹棳偲偟偰儕僯傾側揹棳側偺偱偡偑儕僯傾擖椡偵報壛偟偰偄傞揹埑偑巒傔偐傜2偺傋偒忔偺EXpo KBD CV側偺偱弌椡揹棳傕Expo偲偄偆偙偲丅
CV偑0V偱側偗傟偽Vbe2偺摦嶌揰偵墳偠偰Ic1偑忔彍嶼偝傟偨抣偑Ic2偲側傝傑偡偑Hz/V擖椡偺KEY CV偺摍斾娫妘偵曄壔偼偁傝傑偣傫丅
Log amp:丂丂丂丂Vbe=Vt*Ln(Ic/Is) .......(1)
antilog amp:丂丂Ic=Is* EXP(Vbe/Vt) .....(2)
偲側傝(2)偺Vbe偵(1乯幃傪戙擖偡傞偲EXP偲Ln偑憡嶦偝傟傑偨Vt偑憡嶦偝傟傞Oct/V擖椡偵偍偗傞Vt偺塭嬁偼偁傝傑偣傫丅丂偝傜偵偼Is傕憡嶦偝傟偰偄傑偡丅丂
Ic = Is * EXP(Vt*Ln(Ic/Is) / Vt)
丂 = Is * EXP(Ln*(Ic/Is))
丂 = (Is * Ic) / Is
|
儕僯傾 CV IN偵懳偟偰偼Vt偑徚偊傞偺偱壏搙曄壔偵懳偟偰偼塭嬁偟側偄偺偐偲巚偄偒傗忋幃偑惉傝棫偮偺偼Vbe1 亖 Vbe2偺帪偩偗偱偡丅偡側傢偪椉Tr.偺摦嶌揰偑摨偠応崌偺傒側偺偱摉慠Iref偺埵抲丅Oct/V擖椡偺儀乕僗偵揹埑偑偐偐偭偰偄傟偽椉Tr.偺摦嶌揰偑堎側傞偺偱偆傑偄嬶崌偵忋婰偺傛偆偵Vt偑徚嫀偝傟傑偣傫丅偨偩儕僯傾擖椡懁偺CV偺捈慄曄壔偵偨偄偡傞Antilog弌椡偼懳悢-巜悢曄姺偱摨偠偔捈慄曄壔偱偁傞偙偲偼曐帩偝傟傑偡丅 Oct/V擖椡懁偵CV偑偐偐偭偰偄傞応崌偼儕僯傾擖椡偱偁偭偰傕Vt偺戝偒偝偵墳偠偰壏搙偺塭嬁傪庴偗Antilog OUT偺捈慄偺孹偒偑憹戝偟傑偡丅Oct/V懁偺CV偑戝偒偔側傞傎偳奼戝偟偰偄偒傑偡丅摦嶌揰偺嵎偵斾椺丅 偙傟偩偲儕僯傾擖椡懁偵EXPO摿惈偺 KBD CV傪擖傟偨応崌丄壒抯偵側傞偐偲巚偄偒傗儕僯傾擖椡偵EXPO曄壔偺CV傪報壛偟偰偄傞偺偱捈慄偺孹偒偑曄傢偭偰傕EXPO偺僀儞僞乕僶儖帺懱偼塭嬁偟傑偣傫丅偡側傢偪偙偺捈慄偺孹偒偼奐巒OFFSET偵斀塮偼偟傑偡偑丅椺偊偽儕僯傾擖椡 1V/2V/4V/8V偺曄壔偵懳偟偰4V偲8V偺帪偺Output偺揹棳攞棪丄摨條偵2V偲4V丄1V偲2V偺攞棪偼2攞偱曄壔偟側偄偺偱壒抯偵偼側傝傑偣傫偑揹棳抣偵Offset偑晅偄偰偟傑偄傑偡偺偱婎弨抣偑偢傟傞偲偄偆偙偲偱偡丅 Oct/V CV=0偱偼Vt偑僉儍儞僙儖偝傟傞偺偱0偱偡偑OCT/V懁偵1V傪報壛偟偰antilog偵18mV傪壛偊偨応崌丄 0亷偐傜40亷偺曄壔偱敿壒偪傚偄僺僢僠偑忋偵偢傟傞掱搙偲側傝傑偡丅摉慠OCT/V 偵戝偒側揹埑傪偐偗傟偽偝傜偵偢傟傑偡偑antilog懁偵揹埑傪僾儔僗偺揹埑傪偐偗偰偄傞偺偱僺僢僠傪偁偘傞偺偑栚揑偱偁傝尦偵傕偳偟偰0V偵偡傟偽儕僯傾擖椡懁偺弌椡偼2偭偺Tr.偺摦嶌揰偑堦抳偟偰壏搙偺塭嬁傪庴偗側偔側傞傢偗偱偡偟幚梡揑側斖埻傪峫偊偰傕壏搙偲僺僢僠偺偢傟偼嫋梕斖埻偐偲丅婎杮壒奒偲偟偰偺偢傟偼側偄傢偗偱偡丅
KORG偺VCO偺antilog偼偙偺傛偆偵曄懃揑側巊梡朄偱偡偑偙偙偱KORG偺傛偆偵儕僯傾擖椡偵Expo KBD CV傪擖傟傞偺偱側偔儕僯傾CV傪擖傟儕僯傾側Ic偺弌椡傪峴偭偨応崌偱傕Vbe2=Vbe1偱側偔Vcv偵揹埑傪壛偊傞偲忋婰偺傛偆偵壏搙曄壔偱孹偒偺堎側傞弌椡傪摼偙傟偼壏搙偑崅偄傎偳孹偒偑偍偍偒偔側傞丄偡側傢偪antilog AMP偵偍傞壏搙偵傛傞僗僷儞偺掅壓偲媡偺斀墳偱偁傝偙偺摦嶌偲傕偆堦偮偺antilog AMP偺慻傒崌傢偣偱偙偺孹偒傪挷惍偡傟偽Vt偺梫慺傪僉儍儞僙儖偱偒傞偙偲偵側傝傑偡丅 忋偺曽偱彂偄偨Hillwood偺SY1800偺antilog曗彏偼Vt偵斾椺偟偨揹埑傪敪惗偡傞夞楬傪巊偭偰KBD CV偲忔嶼傪峴偆偙偲偵傛偭偰antilog偺Vt偺塭嬁傪僇僢僩偡傞曽朄偱偡偑偙偺応崌偼忔嶼婍偑撪憼偝傟偨Vt揹埑敪惗夞楬偲偟偰婡擻偟傑偡丅偙傟偼杮幙揑偵偼2偭偺摦嶌揰偱摦偄偰偄傞2偭偺Tr.偺Ic偲Vbe偺娭學偲Vt偺娭學傪偆傑偔巊偭偨夞楬偵懠側傜側偄偺偱偟傚偆丅偡側傢偪Iref傪屌掕偟偰偦偙偑奐巒揰偵側偭偨帪傕偆堦曽偺摦嶌揰忋偵偄傞Tr.偺Ic偲Vbe偲Vt偺娭學偱偡丅拞乆墱偺怺偄夞楬丅偲偄偆偐Ic偲Vbe偺幃偑慡偰傪暔岅偭偰偄傞偺偱偡偑丅 暿偺page偵傕彂偒傑偟偨偑MS偺antilog Tr. 2SC1583偵偼價僯乕儖僉儍僢僾偑偮偗傜傟偰偁傞掱搙偺壏搙曗彏偲偄偆偐壏搙曄壔傪娚榓偡傞慬抲偡傞慬抲偑側偝傟偰偄傑偡偑偙偺岠壥偼偼偨偟偰Oct/V偵懳偟偰偺慬抲側偺偐偙偲偵傛傞偲忋婰偺儕僯傾CV懳墳側偺偐偲傂偦偐偵巚偭偰偟傑偄傑偟偨偑....丅 |
堦斒揑側 Oct/V偺 antilog 偲 MS偺 antilog偺堘偄偼丄Q1偺Vbe偑堦斒偺 antilog偑屌掕偵側傞偺偵懳偟偰 MS偺antilog偼 KEY CV偺曄壔傪庴偗偰曄摦偟傑偡丅丂Q2偺Vbe偺曄壔偼椉幰偱摨偠偱偡丅
antilog AMP偺挷惍
MS20/10偺VCO偺挷惍偺崁傪尒傞偲Pitch Adj.偲OP AMP偺 offsetnull挷惍偺2偭偺POT偵傛傝孹偒偲OFFSET傪挷惍偡傞傛偆偵側偭偰偍傝 Pitch Adj,傪Tune HIGH, offset null傪Pitch LOW挷惍偲屇傫偱偄傑偡丅丂MS50偱偼OCT/V偺SPAN挷惍偑捛壛偝傟偰偄傑偡偑丆MS20/10偱偼SPAN挷惍偼CV擖椡偺VR偱愝掕偡傞傛偆偵側偭偰偄傑偡丅丂偙傟偼MS20/10偱偼婎杮antilog(Oct/V擖椡)偺Scale壏搙曗彏偑娙棯壔偝傟偰偄傞偙偲傊偺懳張偩偲巚傢傟傑偡丅
傑偢偼堦斒揑側antilog AMP偵偍偄偰偼 Oct/V擖椡偵懳偟偰偺壒奒偺摍斾楍傪寛傔傞SPAN(SCALE)挷惍偲尞斦偲VCO敪怳廃攇悢偺懳墳傪寛傔傞OFFset挷惍偑偁傝傑偡丅丂MS偺antilog偵偼偦傟偵壛偊偰 OP AMP偺 Offset null挷惍偑偮偄偰偍傝偙傟傪Tune LOW偲偟偰偄傑偡丅丂傑偨Oct/V偺OFFSET傪Tune HIGH偲屇傫偱偍傝椉幰偺挷惍偱Key偵懳偡傞VC偺幚敪怳廃攇悢丄Octave娫偺岆嵎傪挷惍偡傞傛偆偱偡丅
偙偙偱堦斒揑側antilog偵偼 OFFsetnull挷惍偼偁傝傑偣傫偑MS偵偼側偤偐偮偄偰偄傑偡丅丂Oct/V偺SPAN挷惍偲偟偰偼報壛偝傟偨 CV傪18/1000偵暘埑偡傞偺偑SPAN挷惍偱偡丅丂 Hz/V KBD CV偵懳偟偰偼偙偺 SPAN挷惍偑婎杮偄傜側偄偺偵OFFset Null偑昁梫偱偐偮偦傟偑Tune LOW愝掕偲尵偆偺偑側傫側偺偐丅
忢壏偱 antilog揹棳偺娭學幃偼丄
丂俬c2=俬ref{倕倶倫((CV)/26mv)}
偙傟偵懳偟偰OP AMP偺OFFset Null偑偁傞応崌偼丄
丂俬c2=(俬ref+Inull){倕倶倫(CV/26mv)}
偲側傝丄 Iref偺曄壔偲偼暿偵offset null挷惍偱敪惗偡傞俬null偲尵偆屌掕抣偺揹棳抣偑晅偔偙偲偵側傝傑偡丅丂OP AMP偵偍偄偰棟憐揑偵偼偙偺抣偼0偱偡偑幚嵺偼敪惗偡傞偨傔偦傟傪0偵偡傞偲偄偆偺偑栚揑偺 POT偩偲巚傢傟傑偡丅
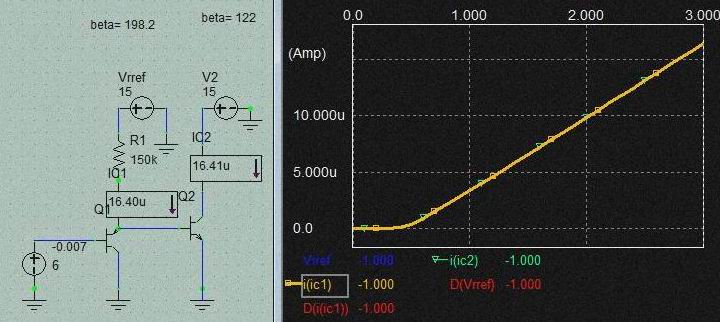
偟偐偟KORG埲奜偺antilogAMP傪搵嵹偟偨synth偵偍偄偰偼偙偺 null挷惍pot傪搵嵹偡傞婡庬偼傎傏懚嵼偟傑偣傫偺偱偙傟偼 Hz/V synth摿桳偺傕偺側偺偱偟傚偆偐丠丅丂傑偢偼偙偺抣偑晅壛偝傟偨応崌偺 antilog嬋慄偑偳偆側傞偺偐傪峫偊偰傒傑偡丅
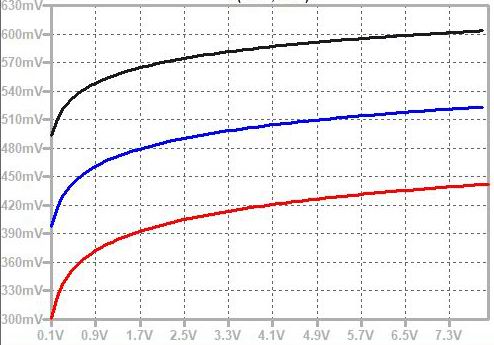
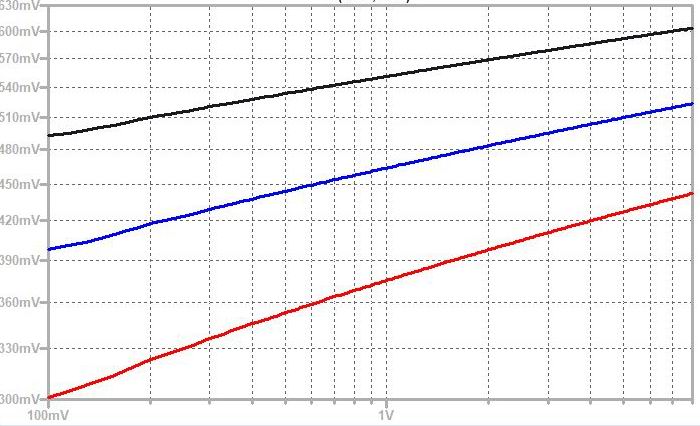
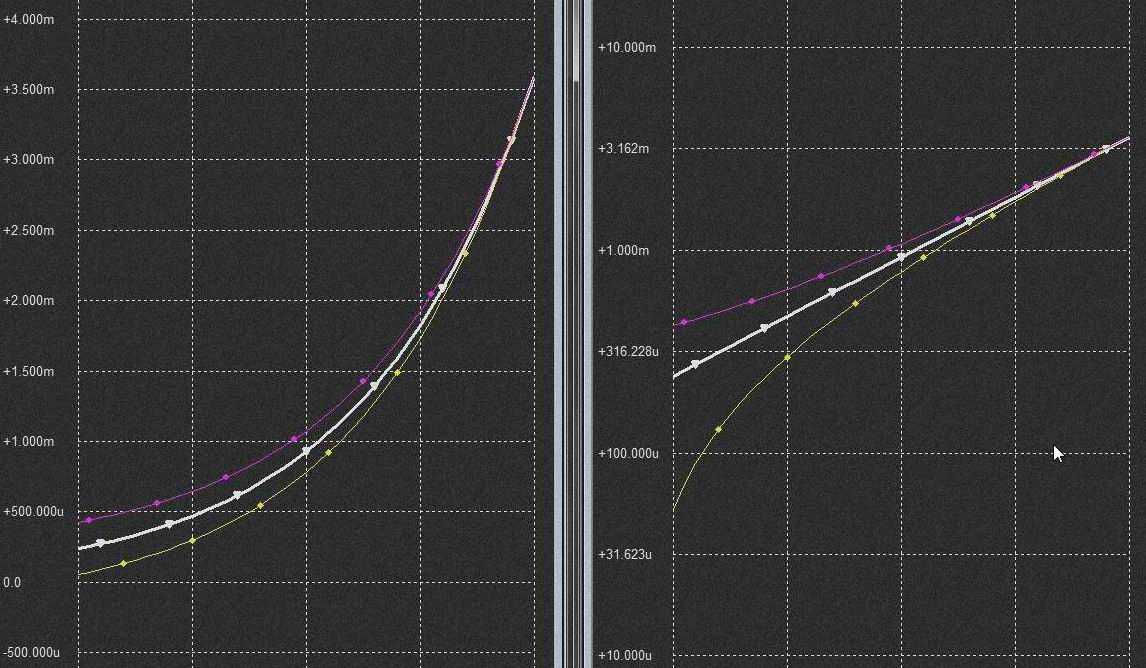
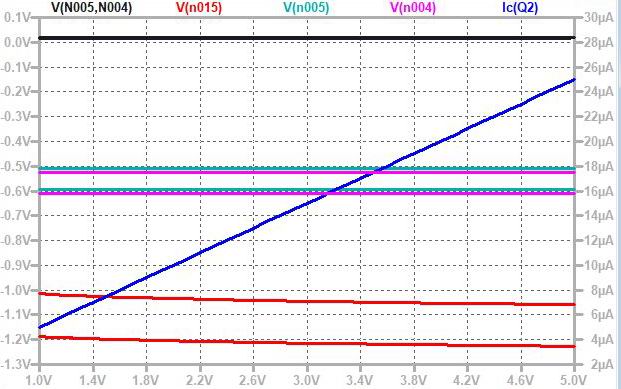
嵍偑Y幉儕僯傾丄塃偑LOG僗働乕儖偱偡丅丂儕僯傾僗働乕儖偱偼傛偔傢偐傝傑偣傫偑LOG僗働乕儖偱尒傞偲Hz/V擖椡偺KEYCV偱嶌傜傟偨壒奒偺摍斾嬋慄偑捈慄曄壔偱側偔掅偄曽偱僗僩儗僢僠偑偐偐偭偰偄傞偺偑妋擣偱偒傑偡丅丂偙傟偼Hz/V KBDCV偵傛傞EXPO僇乕僽偲屌掕揹棳抣(Inull)偺壛嶼側偺偱EXPO僇乕僽懁偺揹棳抣偑偪偄偝偔側傟偽側傞傎偳屌掕揹棳抣偺塭嬁傪庴偗偰偄傞偙偲傪帵偟偰偄傑偡丅丂恾拞偺僺儞僋偺僇乕僽偼屌掕揹棳抣偑僾儔僗偺応崌偱偡偑 EXPO偑0偵嬤偔側傟偽僇乕僽偼悈暯慄偵側傝丄傑偨墿怓偺僇乕僽偼屌掕揹棳抣偑儅僀僫僗偺応崌偱偡偑摨條偵EXPO偑彫偝偔側傞偲僇乕僽偼Y幉傪慟嬤慄偲偟偰摦偒傑偡丅丂椉幰偲傕EXPO嬋慄偺揹棳抣偑戝偒偔側傟偽杮棃偺捈慄曄壔偺僇乕僽偲側傝傑偡丅
Hz/V擖椡偵壒奒scale傪帩偭偨KEYCV傪擖傟傞偲KEYCV偺scale偑姰帏偱傕忋婰Inull偑0偱側偗傟偽掅堟偱僇乕僽偑嬋偑偭偰偟傑偄摍斾娭學偑偢傟傞偺偱 OP AMP偺offset null傪挷惍偡傞昁梫偑偁傞丅丂偝傜偵偼MS synth偵偍偄偰偼偙偺僗僩儗僢僠傪巊偭偰antilog偲尵偆傛傝偼VCO懁傕娷傔偨僩乕僞儖偱偺僩儔僢僉儞僌挷惍傪峴偭偰偄傞傕偺偲巚傢傟傑偡丅丂杮棃偱偁傟偽OP AMP偺 offset傪0偵偡傞婡擻傪僗僩儗僢僠嶌梡傪棙梡偟偰僩乕僞儖僩儔僢僉儞僌挷惍偵巊偆偲偄偆儐僯乕僋側愝寁偱偼側偄偐偲巚傢傟傑偡丅
丂MS偺Iref嵟彫抣: KEYCV=1V Rref=800K.......... 1.25uA(Oct/V in=0V)
丂MS偺Iref嵟戝抣: KEYCV=8V Rref=100K............ 80uA(Oct/V in=0V)
Key CV=1V乮嵟掅偺C偺Key)偱 OCT 32feet帪 Iref偑1.25uA偲側傝傑偡偺偱偙傟偑偙偺偲偒偺 antilog out偲側傝傑偡丅丂
捠忢偺 Oct/V僔儞僙偵偍偄偰偼Iref偼屌掕偱偁傞偺偱 偙偺揹棳offset偼扨偵Iref偑懡彮憹尭偡傞偩偗偺偙偲偱偡偐傜丄Oct/V擖椡偵揹埑傪報壛偡傞偙偲偱夝徚偱偒傞傢偗側偺偱 offset null挷惍偼偄傜側偄偺偱偟傚偆丅
|
偪側傒偵 Oct/V僔儞僙偺 Iref偺抣偼偲尵偆偲丄ROLAND偺100MM VCO偱偼
丂Iref: 10V/100K ...............100uA 偲Iref偼戝偒偄偱偡偑幚嵺M180 KBD偺嵟掅Key偺 CV=1V帪偵initial偺OFFset偲偟偰antilog AMP偵 栺-6V偑偐偐偭偰偄傞偺偱偙偺帪 antilog AMP偺Oct/V擖椡偵偐偐傞揹埑傪-5V偲偡傞偲偙偺帪偺antilog揹棳弌椡偼栺3.3uA偲側傝MS偺栺3攞掱搙偵側偭偰偄傑偡丅 |
* 梋択
|
* 傕偆堦偮偺 Expo Converter
OP AMP + Dual Tr.偺antilog AMP偲嫟偵桳柤側夞楬偲偟偰 ARP曽幃偺僄儈僢僞僼僅儘儚偲偟偰偺PNP丄+ NPN偺儅僢僠僪儁傾Tr.傪巊偭偨夞楬偑偁傝傑偡丅丂偙偪傜偺夞楬偼傛傝僔儞僾儖側峔惉偱偡偑婎杮尨棟偼摨條偵僄儈僢僞僼僅儘儚傪壏搙僙儞僒乕偲曗惓夞楬偵偡傞傕偺偱EXPO摿惈帺懱偼師抜偺 Tr.偺摿惈傪棙梡偟傑偡丅(壓恾丅NPN, PNP偺媡峔惉傕偁傝) 偨偩偟夞楬偼扨弮偱傕摦嶌尨棟偼偙偪傜偺曽偑暋嶨偱偡丅(*1)丂偙偺夞楬偱偼壏搙曄壔偵懳偟偰Ic偼姰慡偵屌掕偱偒偢傢偢偐偵曄壔偟傑偡丅 媡偵夞楬偺峔惉忋Ic偑曄壔偟側偄偲NPN偺Vbe傕曄壔柍偟丄傕偟偦偆偱偁傟偽壏搙曄壔傪NPN偺Ic2偼傕傠偵偆偗偰偟傑偄傑偡偺偱丅 偙偺夞楬偼忋婰偺OPAMP偲Dual Tr.傪巊偭偨夞楬傛傝傢偐傝偵偔偄偱偡丅Dual Tr.偺夞楬偺曽偼僙儞僒乕懁偺Tr偺Ic1傪屌掕偡傞偙偲偵傛傝* OFFSET曗彏偺僌儔僼偺傛偆偵Vbe1偑曄壔偟偰師抜偺Vbe傪曄壔偝偣摦嶌揰傪曄壔偝偣Ic偑屌掕偡傞偲偄偆傢偐傝傗偝偑偁傝傑偡丅偡側傢偪OPAMP偺夞楬偺曽偼摦嶌偑撈棫偟偰偄偰Ic傪堦掕偵曐偮偺偼OPAMP偺晧婣娨斀墳偱Ic偑屌掕偝傟傞偙偲偵傛傝Ic偑屌掕側偺偩偐傜Vbe偺摦嶌揰偑壏搙忋徃偵懳偟偰-2mV偲偄偆偐棟憐抣暘壓偑傞偙偲偵傛偭偰摨條偵師抜偺Tr.偺摦嶌揰傕曄傢偭偰Ic偑屌掕偝傟傞偲偄偆僟僀儗僋僩側斀墳丅 偙偪傜偺曽偼摦嶌偑廳忯偝傟偰偄傞丅壏搙忋徃偱曄壔偑偁傞偲Ic1偺憹壛曄壔偑敪惗偟偰偦傟偑100%晧婣娨偲側偭偰Vbe傪媡曄壔偝偣偰Ic1偺曄摦傪傢偢偐偵梷偊傞丅偙偺応崌傕Ic1偺曄摦偑偍偝偊傜傟傞偙偲偵傛偭偰Vbe1偼Ic1偑屌掕抣偵嬤偄偺偩偐傜Vbe1偺摦嶌揰偑忋婰偲摨條偵壓偑傞偺偩偑Ic1偑姰慡偵屌掕偵側偭偨傜Q2偺Vbe2偼曄壔偣偢壏搙曗彏偵側傜側偄偺偩偑偙偺応崌 +儮Ic1* Re1 = -儮Vbe1偲側傞傛偆側偩偗Ic1偑憹偊傞傢偗側偺偱Vbe1偺摦嶌揰偼杮棃偺栚揑抣偐傜傢偢偐偵忋徃丄偦傟備偊Ic1傕傢偢偐偵忋徃偟偰偦傟偑Ic1姰慡屌掕偵斾傋偰Vbe1偑壓偑傝愗傜側偄寢壥偲側傝暯峵偟傑偡丅 偙傟偼忋婰偺壏搙曗彏偺僌儔僼偵偍偄偰壏搙曄壔偱傢偢偐偵Ic偑忋徃偡傞偙偲偼Vbe偺壏搙曄壔偑-2mv/亷傛傝傢偢偐偵払偟側偄偱暯峵偟偰偄傞偙偲傪堄枴偟傑偡丅
側偤PNP + NPN偺峔惉側偺偐丄壖偵 NPN僄儈僢僞僼僅儘儚 + NPN Tr.偺峔惉偩偭偨応崌丄壏搙曄壔偱嚈Vbe1偑掅壓偟偰僄儈僢僞僼僅儘儚弌椡偑忋徃偟偰偄傑偄壏搙曗彏偵偼側傝傑偣傫丅偡側傢偪僄儈僢僞僼僅儘儚偺嚈Vbe1偼掅壓偟偰弌椡傕掅壓偡傞峔惉偵偡傞堊偵偼 PNP + NPN 偐 NPN + PNP 偺慻傒崌傢偣偑昁梫側偺偱偡丅丂摨峔惉偺Tr.傪巊偄偨偗傟偽 OP AMP偺応崌偲摨條丄嵎摦峔惉偵偟側偗傟偽側傝傑偣傫丅 偦偺応崌 OP AMP傪徣棯偟偨宍偺暔傕傛偔偁傝傑偡丅 傑偨CV忋徃偵懳偟偰Ic1偼儕僯傾偵掅壓偟傑偡偑僄儈僢僞僼僅儘儚弌椡揹埵偼PNP Tr.偺偨傔 Vcc - R2*Ic1偵側傝儕僯傾偵忋徃偟傑偡偺偱偦傟偵愙懕偝傟偰偄傞NPN Tr.偺Vbe偼儕僯傾偵憹壛偟傑偡丅丂偙傟偵傛偭偰忋婰偺 OP AMP偺 antilog偱偼慜抜偵斀揮憹暆婍偑堦偮昁梫偩偭偨偺偑徣棯偝傟偰偄傞偲偄偆媄傕擖偭偰偄傑偡丅
傛偭偰偙偺夞楬偱偼Ic偼僄儈僢僞僼僅儘儚偺壏搙摿惈暘偺曄摦偑偁傝壏搙偑忋偑傟偽Ic偑憹偊丄嚈Ic1 * R2 暘偩偗 Vbe1偑掅壓偟傑偡丅丂偦偟偰偙偺嚈Vbe1暘偺掅壓偑NPN Tr.偺Vbe2偵斀塮偝傟椉 Vbe偑摨偠偩偗掅壓偟傑偡丅丂NPN偺Ic2偺曄摦暆偼 PNP偺Ic1偺曄摦暆偲摨偠偵側傝 PNP偺壏搙曗彏摿惈偑 NPN偵宲彸偝傟傞偲偄偆峔憿偵側偭偰偄傑偡丅丂偙偺晹暘偑OP AMP偺 antilog偲摨偠偱偡丅
CV 0V偺帪 Q1(PNP)偲 Q2(NPN)偼儅僢僠僪儁傾偲偄偆慜採側偺偱偙偺帪椉C-E娫傪棳傟傞揹棳偼 摨偠偱 Ic1 = Ic2
Vbe1 = Vb2 - CV = Vb2 - Vb1
Ic2/Ic1 = Is/Is * exp((Vb2 -(Vb2 -Vb1)/Vt) 偲側傝Is偼徚嫀偝傟傑偡偑Ic2偺EXPO僇乕僽偵偼 Ic1偡側傢偪 CV=0V帪偺Ic1偺崁偑偮偒傑偡丅丂偙偺Ic1偼忋婰偺捠傝壏搙偵傛偭偰懡彮曄摦偟偙偺曄摦暆偼僄儈僢僞僼僅儘儚偺壏搙摿惈偲側傝傑偡丅丂傑偨OP AMP偺antilog偲摨偠傛偆偵 CV=0V帪偺偙偺Ic1偺抣傪Iref偲偡傟偽 CV抣偵傛傞Ic2偺抣偑傢偐傞偲偄偆偙偲偱偡丅 OP AMP斉偺傛偆偵Ic偑姰慡偵屌掕偟偰偄傟偽壏搙偺塭嬁偼Vbe偵100%尰傟Vbe偑曄摦偟偨帪偺Ic偺抣偑壏搙偵塭嬁偝傟側偄抣偲摨偠偵側傝傑偡偑偙偺応崌偼Ic偺旝彫曄摦偱偡偑曄壔揹埑偼嚈Ic1 * R2側偺偱Vbe偲偟偰偼偦偙偦偙曄摦偟偦偺抣偼Ic屌掕帪偲傎傏摨偠偲偄偆岻柇側夞楬偱偡偑偪傚偭偲僩儕僢僉乕偵傕巚偊傑偡丅丂嚈Ic偲嚈Vbe偑摨偠 晧婣娨儖乕僾撪偵偁傞偺偱惂栺忦審傪枮偨偡傛偆偵摦嶌偡傞偲偙偺傛偆側寢壥偵側傞偺偑柺敀偄丅
* 摦嶌斖埻
傎傏OP AMP偺 antilog偲摨偠摦嶌傪彮側偄晹昳偱峔惉偟偰偄傞丅丂傢偐傝偵偔偄偺偼CV偺曄壔偱偼Ic1偑儕僯傾偵曄壔偡傞偑丄偙偺帪Vbe1偼旝彮曄壔偱幚幙曄壔偟側偄偲埖傢傟傞丅丂壏搙曄壔偵懳偟偰偼傎傏Ic1偼曄壔偟側偄偺偱嚈Vbe1偑偦偺暘掅壓偡傞丅丂Ic1偑慡偔曄壔偟側偄偲偙偺夞楬偼峔惉忋偮偠偮傑偑崌傢側偄偺偱旝彮偺曄壔偑偁傞丅丂偡側傢偪晧婣娨偵傛傝Ic偺曄摦棪8%偑嚈Vbe1 =栺2mV偵嬤偄抣傪偲傞偵懌傝傞嚈Ic1偺抣偵偍偝傑傞傛偆偵暯峵偟丄R2*嚈Ic1 = -嚈Vbe1偲側偭偰 NPN偵懳偟偰偟偰偙偺曄壔偑OFFSET壏搙曗彏偵側傞丅
|
|
丒梋択2
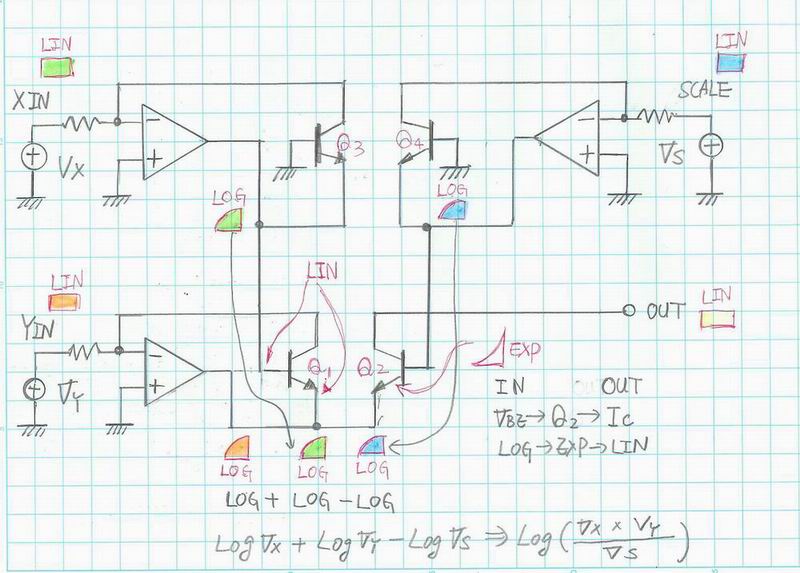
丒antilog amp偲 log amp傪巊偭偨 忔嶼婍 antilog amp偺墳梡偲偟偰偼log amp偲儁傾偱巊偆偲1徾尷偺忔嶼婍傪嶌傞偙偲偑偱偒傑偡丅 偙傟偼IC偺RC4200偺峔憿偦偺傕偺偱偡丅 antilog amp偺儕僯傾擖椡偵揹埑傪報壛偡傞偲OPAMP弌椡(Ve)偼LOG曄壔偵側傝傑偡丅 偙偺偨傔Yin擖椡晹暘偺 OP AMP偲Q1偺峔惉晹暘偩偗偲傟偽Log amp偱偡偑Q2偺Vbe偲Ic偺娭學偼EXPO側偺偱 Ic2偼偙偺応崌LINEAR弌椡偵側傝傑偡丅 摨條偵Xin懁偺OPAMP偲Q3偺峔惉偼Log amp偲偟偰摦嶌偟傑偡偑Q1偺儀乕僗偵報壛偝傟傞揹埑偱Q1偺Vbe1偼曄壔偟傑偣傫偺偱報壛偝傟偨揹埑偼偦偺傑傑Q1偺僄儈僢僞偵揱払偝傟傑偡丅偙偺晹暘偑廳梫偱偡丅堦曽 Scale in懁偺 OPAMP偲Q4偱峔惉偝傟傞夞楬傕Log amp偱偡丅偙偺弌椡偼Q2偺儀乕僗偵擖傝傑偡偑Q1偺儀乕僗偵報壛偝傟偨揹埑偺帪偺傛偆偵Vbe1偑曄壔偟側偄偙偲偼側偔Q2偺Vbe偼摉慠偙偺儀乕僗偺揹埑偱曄壔偟傑偡丅 Antilog擖椡偼Q1偲Q2偱偁傝Q1偼儅僀僫僗擖椡丄Q2偼僾儔僗擖椡偱偡偑奺Log AMP偼儅僀僫僗弌椡側偺偱Q1偵懳偟偰偼壛嶼偵側傝Q2偵i懳偟偰偼尭嶼偵側傝傑偡丅傑偁Q1偲Q2偺峔惉偑嵎摦側偺偱偁偨傝傑偊側偺偱偡偑寢嬊丄Q2偺僄儈僢僞偑X偲Y偺Log OUT偱憹壛丄Q2偺儀乕僗偑scale偺LogOUT偱掅壓偡傞偲偄偆偙偲偱偡丅傑偨奺Log OUT偼僾儔僗偵偼側傝傑偣傫丅
Q2偺摦嶌揰偺堏摦乮Vbe乯偲偟偰偼 Log Xin + Log Yin - Log Scale偱 Q2偺Vbe偑曄壔偟傑偡偺偱 偙傟偑 Q2偺 Vbe偲Ic偺娭學偑 EXPO偲偄偆偙偲偱Log * Exp (惓妋偵偼Ln * Exp )偱 Log偲Expo偑庢傟偰儕僯傾側 Vx* Vy /Vs偵側偭偰忔嶼偑偱偒傞偲偄偆偙偲偱偡丅 忋婰偺MS20偺antilog夞楬偱偼儕僯傾擖椡偲EXPO擖椡偺墘嶼偱壏搙曄壔偵懳偟偰偺塭嬁偑偱傑偟偨偑偙偺夞楬偵偍偄偰偼塭嬁傪庴偗傑偣傫丅
|
<2026/02/24 rev1.14>
<2025/09/21 rev1.13>
<2021/03/02 rev1.12>
<2019/10/29 rev1.11>
<2019/08/13 rev1.10>
<2019/06/04 rev1.9>
<2019/05/06 rev1.8>
<2019/05/05 rev1.7>
<2018/08/15 rev1.6>
<2017/07/18 rev1>