1:丂FM婎杮尨棟
2:丂analog FM
3:丂FM偲PhaseModulation
4:丂FM偲攞壒
5:丂Linear FM偲EXP FM
6:丂FM偲phase modulation偺堘偄
Digital壒尮偱偼偍側偠傒偺FM曄挷傕 analog synth偱幚尰偱偒傑偡丅丂VCO傪audio懷堟偺惓尫攇偱曄挷偡傟偽FM曄挷偵側傞傢偗偱偡偑丄扨弮偵 oct/V偺 VCO傪曄挷偟偨応崌偼exponential側 FM曄挷偵側傝偙傟偼 analog synth偱偼 X- mod.側偳偲屇偽傟 ring modulator揑側岠壥傪嶌傝弌偡応崌偵巊梡偝傟傑偡丅
exponential FM曄挷偼曄挷攇偱曄挷傪偐偗傞偲尦偺僺僢僠偑曄壔偟偰偟傑偆 偺偱丄僺僢僠傪曄壔偝偣側偄偱壒怓偺傒曄壔偝偣偨偄応崌偼丂linear FM曄挷偲偄偆曽朄傪梡偄傑偡丅丂偙傟偼 VCO偺 Hz/V擖椡偵曄挷攇傪擖椡偡傞偙偲偱幚尰偱偒丄婎杮揑偵偼 Digital 壒尮偺 FM偲摨偠尨棟偱摦嶌偟傑偡丅丂偡側傢偪曄挷攇偱曄挷傪偐偗偰傕僺僢僠傪曄壔偝偣偢攇宍傪曄壔偝偣傞偙偲偑壜擻偱偡丅
曄挷傪偐偗傟偽VCO偺僺僢僠偑摦偔偺偑偁偨傝傑偊偱曄壔偟側偄偺偼傊傫偲巚傢傟傞偐傕抦傟傑偣傫丅丂 偦偺尨棟偼屻偱愢柧偡傞偲偟偰丄偄傢傫偲偟偰偄傞偙偲偼曄挷偝傟傞懁偺敪怳婍(僉儍儕傾)偲曄挷梡偺敪怳婍(儌僕儏儗乕僞)偺敪怳廃攇悢傪摨偠(偐惍悢攞)偵偟偰丄椉幰偺敪怳婍偵偼廃攇悢偺弶婜愝掕梡 CV偺懠偵 Key CV傪偮側偓傑偡丅丂偦偟偰曄挷梡偺敪怳婍偱僉儍儕傾偵懳偟偰曄挷傪偐偗傑偡丅
偙偺応崌 key CV偱壒掱忣曬傪椉敪怳婍偵梌偊偰傕偪傖傫偲椉敪怳婍偼僩儔僢僉儞僌偟偰摦偔偲偄偆偙偲偱偡丅丂曄挷偑尨場偱椉幰偺僺僢僠偑偢傟傞偲尵偆偙偲偼婎杮揑偵偁傝傑偣傫丅丂扐偟偙偺傛偆偵摦嶌偝偣傞偨傔偵偼摿掕忦審偑枮懌偝傟側偗傟偽側傝傑偣傫丅
摿掕忦審偲偼丂曄挷攇偑僉儍儕傾偺惍悢攞偵偁偭偰曄挷攇偺怳暆曄壔(攇宍怳暆偺旝暘抣)偺+偲- 偺榓偑0偱偁傟偽僉儍儕傾僺僢僠偼曄壔偟傑偣傫丅
偙傟偼捠忢偺斃憲攇偵曄挷怣崋傪廳忯偝偣怣崋揱払偝偣傞偲偄偆FM曄挷偺杮棃偺巊偄曽偐傜偡傟偽摿堎側巊梡曽側偺偱偡偑 壒尮偲偟偰偺FM偱偼婎杮揑側巊偄曽偱偡丅
杮奿揑側FM曄挷偺壒尮偲偟偰偼傗偼傝digital曽幃偵孯攝偑偁偑傞偺偼摉慠側偺偱偡偑丄analog曽幃偺FM偲偄偆偺偼攇宍丄攞壒丄廃攇悢丄敪怳偲偄偭偨偄傠偄傠側婎杮僥乕儅傪娷傫偱偄傞偺偱庢傝忋偘偰尒傑偟偨丅
FM壒尮娭學偺忣曬偼懡乆偁傞偲巚偄傑偡偑堄奜偲偄偆偐丄戝慜採偱偁傞崁栚丄偨偲偊偽 FM 偲phase modulation偺堘偄丄exponential FM偲 linear FM偺堘偄偲偐丄FM偱偼曄挷攇偱僉儍儕傾傪曄挷偟偰傕僺僢僠偑曄摦偟側偄巊梡朄偑偱偒傞偙偲摍偺崁栚偵懳偟偰丄擺摼偱偒傞尨棟愢柧偑側偐側偐尒偮偗傜傟側偐偭偨偺傕偙偙偱偙偺僥乕儅傪庢傝忋偘偨偒偭偐偗偱偡丅
偦傕偦傕偙偺page傪彂偔偒偭偐偗偵側偭偨偺偼偳偆偟偰 analog FM曄挷偵偍偄偰偼 self feedback傪峴偆偲pitch偑曄摦偟偰偟傑偆偺偐偲偄偆媈栤揰偱偟偨丅
偄偔偮偐偺幚椺攇宍
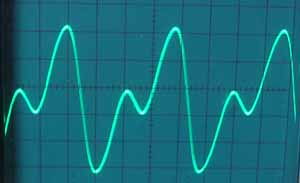
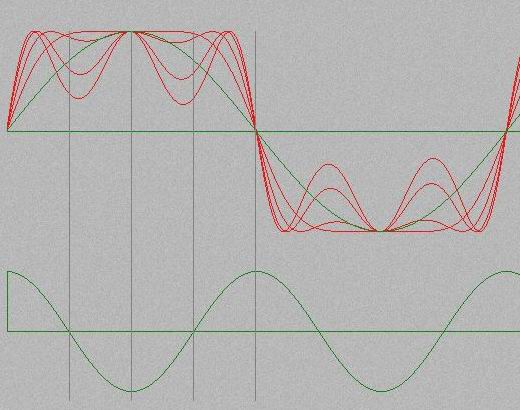
* 僉儍儕傾/儌僕儏儗乕僞廃攇悢斾丂1:1丂曄挷怺搙彫
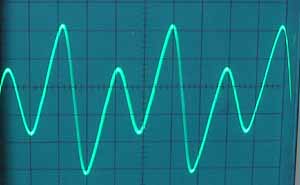
* 僉儍儕傾/儌僕儏儗乕僞廃攇悢斾丂1:1丂曄挷怺搙戝
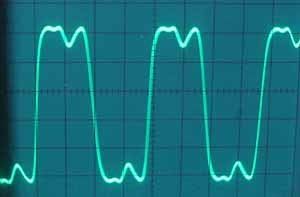
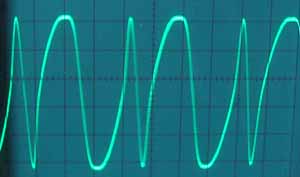
* 僉儍儕傾/儌僕儏儗乕僞廃攇悢斾丂1:2
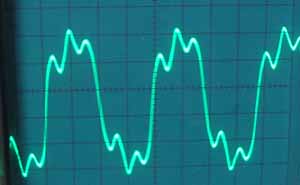
* 僉儍儕傾/儌僕儏儗乕僞廃攇悢斾丂1:3
忋婰偺攇宍偼 analog modeling synth ION偱偺偺Linear FM mode偱偺攇宍偱偡偑analog synth傪僔儈儏儗乕僩偟偰偄傞偺偱phase modulation偱偼側偔FM側偺偱僉儍儕傾丄儌僕儏儗乕僞偺廃攇悢丄埵憡傪崌傢偣傞偺偑側偐側偐戝曄偱偡丅
傑偢偼FM曄挷偺幃偱偡偑,(幃偺惗惉夁掱偼暿婰)
FM曄挷偺幃偲analog VCO偺懳墳
丂E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) }
丂* fm ......儌僕儏儗乕僞VCO偺敪怳廃攇悢丅
丂* Fcl .....僉儍儕傾VCO敪怳廃攇悢丅
丂* 儮F .......柍曄挷帪偺僉儍儕傾VCO偲曄挷帪偺嵟戝(嵟彫)敪怳廃攇悢偺嵎
丂* 儮F/fm丂= m ..... modulation INDEX
儮F偵偮偄偰
-----------------
堦斒揑側FM傗synth偵偍偄偰LFO側偳偱曄挷偟偨応崌偱偼弌椡攇偼曄挷攇偵傛偭偰僺僢僠曄摦傪偆偗傞傢偗偱偦偺嵺丄曄挷攇偺亄怳暆偺僺乕僋抣偱嵟戝敪怳廃攇悢偵側傝丄亅怳暆偺僺乕僋抣偱嵟彫敪怳廃攇悢偵丄0偱僉儍儕傾廃攇悢偵側傞傢偗偱偡丅丂嵟戝敪怳廃攇悢乕僉儍儕傾廃攇悢傕偟偔偼丄僉儍儕傾廃攇悢乕嵟彫敪怳廃攇悢偑儮F偱偡丅 丂嵟戝廃攇悢曃嵎側偳偲屇偽傟傑偡丅
弌椡偺敪怳廃攇悢偼 FM壒尮偺応崌丄儌僕儏儗乕僞偺廃攇悢偑僉儍儕傾廃攇悢偺惍悢攞偵偁傞帪(偐偮曄挷攇怳暆偺旝暘抣偺+,-偺榓偑0偺帪) 偼僉儍儕傾偺敪怳廃攇悢偲摨偠偵側偭偰偟傑偆偺偱偪傚偭偲偙偺昞尰偼偍偐偟偄偲傕偲傟傑偡偑偙偺幃偼FM曄挷偺堦斒幃側偺偱偙偆昞尰偝傟傑偡丅 寢嬊儌僕儏儗乕僞偺怳暆(p-p)偺 1/2偺捈棳揹埑偱偳偺偔傜偄僉儍儕傾VCO偺敪怳廃攇悢偑曄壔偡傞偐偲偄偆抣偲峫偊偰偄偄偺偱偼側偄偐偲巚偄傑偡丅丂梫偼儌僕儏儗乕僞偺傾儅僂儞僩儗儀儖偵憡摉偡傞傢偗偱偡偑丄忋婰偺幃偼 analog synth偺FM偺幃偲偄偆傢偗偱側偔FM曄挷偺堦斒幃側偺偱偙偺儗儀儖傪曄挷怳暆偱偳偺偔傜偄廃攇悢偑曄壔偡傞偐偲偄偆抣乮廃攇悢曃嵎乯偲偟偰掕媊偟偰偄傑偡丅
傑偨儮F/fm傪modulation INDEX 偲屇傃屻偺曽偱帵偡儀僢僙儖娭悢傪巊偭偨攞壒偺嫮搙傪寁嶼偡傞偨傔偺抣偲側傝傑偡丅
1/fm偼儌僕儏儗乕僞(曄挷攇)偺愊暘梫慺偵傛偭偰弌尰偡傞崁偱FM曄挷偑儌僕儏儗乕僞偺廃攇悢偱傾儅僂儞僩儗儀儖偑曄壔偟偰偟傑偆偙偲側偳傪帵偟偰偄傑偡偑徻嵶偼屻偱帵偟傑偡丅
SIN{丂}偺堄枴
----------------------
SIN{丂}偺妵屖偺拞偺抣偼妏搙偱偡丅丂偙偺応崌妵屖撪偺(寁嶼寢壥/360) 偵懳偟偰偺偁傑傝(忚梋)偑 {丂} 撪偺抣偮傑傝妏搙偲夝庍偝傟偦偺SIN偑怳暆偲側傝傑偡丅
2兾(儔僕傾儞)偼360搙偱 墌廃堦廃偩偐傜偦傟偵廃攇悢偲帪娫傪偐偗偨抣偼傗偼傝妏搙偲側傝傑偡丅丂偮傑傝宱夁帪娫t偺妏搙偺椵愊抣偱忋婰偺傛偆偵墌廃偼360搙側偺偱偦傟偱妱偭偨偁傑傝偑偦偺帪娫偺墌廃1廃偵懳偡傞埵憡妏偵側傝傑偡丅
僉儍儕傾偺傒偱曄挷偑偐偐偭偰偄側偄応崌偼扨弮側摍懍墌塣摦側偺偱SIN乷 2兾Fcl*t}偱偡偑SIN攇偱曄挷傪偐偗傟偽摍懍偱偼側偔側傞偺偱偄傢偽SIN攇宍偺僥乕僽儖偺撉傒弌偟偵廃婜揑側恑傒丄抶傟偑弌丄偦傟偺尨場傪曄挷攇懁偺SIN攇偑偵側偭偰偄傞丅
僉儍儕傾偵懳偟偰廃攇悢偺戝曄掅偄曄挷攇偱偁傟偽價僽儔乕僩偲側傝偙偺応崌丄廃婜揑側恑傒抶傟偑挿帪娫懕偔宍偲側傞偺偱偦傟偑偼偭偒傝偲偟偨壒掱偺曄壔偲偟偰昞傟傑偡偑忋婰偺傛偆偵儌僕儏儗乕僞偺廃攇悢傕AUDIO懷堟偺応崌偼僉儍儕傾偺1廃婜偺娫偱偺埵憡偺恑傒丄抶傟偲側傞偨傔攇宍偺曄宍偲偟偰尰傟傞丅
(儮F/fm)*SIN(2兾fm*t)偺崁
-------------------------------------
(儮F/fm)*SIN(2兾fm*t)丂偺堄枴偼SIN(丂)偺斖埻偑 +/-1側偺偱 嵟戝 +/-(儮F/fm) 丂儔僕傾儞丂僆儕僕僫儖偺廃婜偵懳偟偰偙偺抣 (妏搙)偑壛嶼偝傟傞偲偄偆偙偲偱偡丅
偨偲偊偽 偙偺崁偑 0.5偱偁傟偽 (0.5/2兾)*360搙=29搙偱柍曄挷帪偺儕僯傾側埵憡恑峴帪娫偵懳偟偰儕僯傾偵埵憡妏偑憹壛偵懳偟偰嵟戝 埵憡妏偑29搙恑傓偲偄偆偙偲偱偡丅
偦傟偺堄枴偡傞偲偙傠偼妏懍搙偑忋偑傞偙偲偲摨偠側偺偱摨偠帪娫宱夁偱傕偦偺帪偺怳暆偼埵憡偑恑傫偩埵抲偺怳暆傪斀塮偡傞偙偲偵側傝傑偡丅
媡偵埵憡偑嵟戝-29搙抶傟傞婜娫偱偼妏懍搙偑壓偑傞偙偲偵側傞偺偱摨偠宱夁帪揰偱慜偵偁傞埵憡埵抲偺怳暆偑斀塮偝傟傑偡丅
偙偙偱廳梫側偺偼偙偺僾儔僗儅僀僫僗偝傟傞埵憡暘偼堦掕抣偱偼側偔帪娫揑偵曄壔偟偰偄傞偙偲偱偡丅丂堦掕抣偱偁傟偽扨偵恑峴攇宍偵懳偟偰僆僼僙僢僩偑偮偔偩偗偱戝尦偺攇宍恑峴偦偺傕偺偼僆儕僕僫儖偲曄壔偟傑偣傫丅
帪娫揑偵曄壔偟偰偄傞偺偱恑傫偩傝丄抶傟偨傝偑惗偠偰偦傟偑帪娫幉偑埑弅丄怢挿偟偨偲摨偠岠壥傪梌偊偰偄傑偡丅
偝傜偵偙偺曄壔検偑 1廃婜偺斖埻偱偼+/- =0偵側傞応崌偼 1廃婜傪捠偣偽僺僢僠偺曄壔偼側偄偺偱偡丅
fm 偑 Fcl 偺惍悢攞偵偁傟偽 Fcl偺1廃婜撪偱埵憡偑恑傫偱傕偁偲偱埵憡偑抶傟傞偺偱+,- = 0偱慡懱偱偼 Fcl 偺廃攇悢曄摦偼側偟偱偡丅
偙傟偑惍悢攞偱側偄帪偺巊梡朄偑杮棃偺FM曄挷丄偮傑傝斃憲攇偵曄挷攇偲偟偰偺 audio怣崋傪廳忯偡傞巊偄偐偨側傫偱偟傚偆偑丄FM壒尮偱偼偦傟偼旕惍悢攞壒傪敪惗偝偣傞帪偺巊偄曽偲側傝傑偡丅
傑偨 曄挷攇偑僉儍儕傾偺1/2偱偁偭偨傛偆側応崌 Fcl 偺 1僒僀僋儖偱偮偠偮傑偁傢偣偑姰寢偟側偔側傞偨傔 Fcl 偺 1僒僀僋儖傛傝懡偄帪娫偮傑傝 fm偺傕偆堦僒僀僋儖偱 +,- = 0偺摦嶌偑姰寢偡傞偙偲偵側傝傑偡丅丂偙偺応崌惍悢攞偱偼側偄偱偡偑斾椺娭學偵偼偁傞偨傔堦墳 僺僢僠偼僉儍儕傾偺廃攇悢偱暦偙偊傑偡丅(徻嵶偼屻弎)
(儮F/fm)*SIN(2兾fm*t)偺儮F=0偺応崌偼偙偺崁偼堄枴偑側偔側傝傑偡丅偮傑傝 modulation amount 偑 0偲偄偆偙偲偱偡丅丂fm偑0偱偁傞応崌偼偳偆偱偟傚偆丅丂傗偼傝 SIN(丂)偺崁偑0偲側傞偺偱堄枴偑側偔側傝傑偡丅
fm偵娭偟偰偼analog synth偲偺懳墳偱偼偪傚偭偲庍慠偲偟傑偣傫偑丂捈棳偱偁傟偽0Hz側偺偱偙偺幃忋偱偼 0 偩偗傟偳傕捈棳梫慺偼扨偵僉儍儕傾VCO偺敪怳廃攇悢傪寛傔傞梫慺偵側偭偰偟傑偆偺偱偙偺幃偲偼娭學側偄梫慺側偺偱偟傚偆偐丅丂analog synth偵偍偗傞捈棳CV偼堦掕抣偱偁偭偰傕偦傟偑愊暘偝傟傞宍偱敪怳廃攇悢偵塭嬁偡傞傢偗偱偡偑偙偙偱偼偦傟偼僉儍儕傾傪敪怳偝偣傞偨傔偺僷儔儊乕僞偵側偭偰偟傑偆偲尵偆偙偲偱偟傚偆偐丅
0Hz偵偼側傜側偄偑掅懍側LFO偺応崌偼桳岠偱Fcl傛傝fm偑偼傞偐偵彫偝偗傟偽僉儍儕傾偺1廃婜偵懳偟偰偁傞弖娫偼曄挷攇偼偁傞怳暆偱巭傑偭偰偄傞傛偆側傕偺側偺偱偦偺怳暆暘偑僉儍儕傾偺撉傒弌偟妏偵捛壛偝傟偰僉儍儕傾偺廃攇悢偑曄壔偡傞偙偲偵側傞偺偱偟傚偆丅
(摍懍墌塣摦)埵憡偺恑峴偲曄挷攇偺娭學
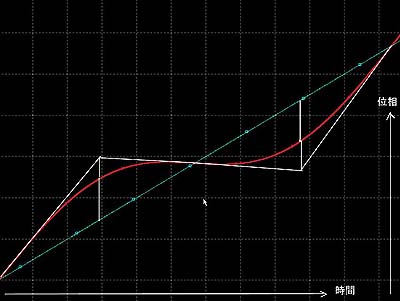
帪娫恑峴偵懳偡傞柍曄挷偺埵憡偺恑峴嬶崌偼堦掕側偺偱偦偺椵嶼抣偲偟偰偺帪娫幉偵懳偡傞埵憡恑峴偼堦掕抣傪愊暘偟偰捈慄忋徃偱偡丅
偦傟偵懳偟偰惓尫攇偺曄挷攇傪壛偊傞偲丂0..90搙偺斖埻偱偼忋徃妏偑偍偍傓偹偁偑傝丄90搙偱柍曄挷偲摨偠丄90搙..270搙娫偱偼孹偒偑壓偑偭偰偄傑偡丅丂270搙..360搙娫偵側傞偲嵞傃妏搙偑忋偑傞傛偆側恑峴偵側傝傑偡丅
偱偡偐傜戝榞0..90搙娫偼埵憡妏偺恑峴偑憗偔偵恑傒僉儍儕傾惓尫攇偺0,..90搙暘傛傝傕偁偲偺妏搙埵抲偵懳墳偡傞怳暆偑惗偠丄90..180搙娫偼埵憡妏偺恑峴偑抶偔側偭偰僉儍儕傾惓尫攇偺偺偙傝偺妏搙偵懳偡傞怳暆偑敪惗偡傞偙偲偵側傝傑偡丅
惓尫攇偱曄挷傪偐偗傞偙偲偼扨弮偵峫偊傟偽曄壔検偼 +, +, - , -偺傛偆側婥傕偟傑偡偑埵憡偺恑峴搙偼惓尫攇偦偺傑傑偺 +, +, -, -,偮傑傝 0..180搙傑偱偼柍曄挷帪偵偔傜傋偰僩乕僞儖偱偼恑傫偱偄偰 180搙偱摨偠偵側傝 180..360搙傑偱偼僩乕僞儖偱偼抶傟偰偄偰360搙偱摨偠偵側傞丅
恑峴嬶崌偺懍偝偺曄壔偼 COS攇偺曄壔偱+,-,-,+偲側傝傑偡丅丂偮傑傝忋婰偺曄挷偑偐偐偭偨捈慄偺孹偒偲摨偠偵側傝偦傟偼曄挷SIN攇傪旝暘偟偨宍偲偄偆偙偲偱偡丅丂
恾偐傜僉儍儕傾偺1廃婜撪偱丄曄挷攇偺曄壔偑憗偄(廃攇悢偑崅偄)曽偑曄挷攇偺忋徃丄壓崀偵嵺偟偰孹偒偑戝偒偔側傞偙偲偑傢偐傝傑偡丅丂偡側傢偪曄挷搙偑崅偄偲偄偆偙偲偱偡丅丂捈棳偺応崌偼孹偒偑僉儍儕傾偺孹偒偲摨偠偵側傞偺偱曄挷搙偼0偲偄偆偙偲偵側傝傑偡丅
壓恾偵曄挷攇偺旝暘曄壔偵懳偡傞僉儍儕傾偺曄宍偺條巕傪帵偟傑偡丅
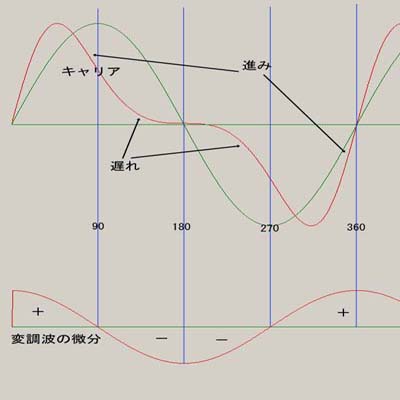
曄挷攇偺旝暘攇宍偑0搙偐傜90搙傑偱偺斖埻偱偼埵憡偑恑傒傑偡偑偦偺曄壔偼堦掕抣偵嬤偄抣偐傜彉強偵棊偪偰偒偰捈慄壓崀偵嬤偔側傞偺偱僉儍儕傾偺攇宍傕偦傟偵墳偠偨曄壔傪偟偰丄巒傔偼恑峴偑憗偄偑偩傫偩傫恑峴偑棊偪偰偒傑偡丅
曄挷攇偺旝暘攇宍偑90搙偐傜180搙傑偱偺斖埻偱偼偙傫偳偼埵憡偑抶傟丄偦傟偵懳偡傞僉儍儕傾攇宍偺撉傒弌偟埵抲偼140搙慜屻偺強偵偒偰偄傞偺偱尦乆偑捈慄壓崀偺攇宍偵側偭偰偄傞偺偱曄挷攇偱曄挷傪庴偗偨攇宍偼曄挷攇偺旝暘攇宍偺宍傪庴偗偮偄偨宍偵曄壔偟偰偄傑偡丅
曄挷攇偺旝暘攇宍偑180搙偵偒偨偲偙傠偱丄僉儍儕傾偺恑傒傕抶傟傕側偔側傝傑偡丅
|
* ANALOG FM analog linear FM偺摦嶌偐傜FM偺幃傪摫偒傑偡丅 analog FM偱偺VCO偺 廃攇悢偲CV偺懳墳偼丄 Vcv = Vcl + Vm* cos(2兾fm*t)
丂丂丂丂丂Vcl: 僉儍儕傾廃攇悢偵懳偡傞CV抣
Fvco =
丂丂丂丂丂Fvco: VCO敪怳廃攇悢
丂丂丂丂丂佺: 0偐傜帪娫t 傑偱偺愊暘
丂丂丂丂丂E(t): FM弌椡偺怳暆揹埑偺帪娫曄壔
曄挷攇偑捈棳偺応崌偼巒傔偺抜奒偱 偙偙偱 儮F = k*Vm丂側偺偱曄挷攇 CV揹埑傪揔摉側傾儅僂儞僩儗儀儖偱報壛偝偣傟偽(儮F/fm)* cos(2兾fm*t)丂偺崁偑摼傜傟傞偲偄偆懳墳偵側傝傑偡丅丂偱偡偐傜CV偺報壛揹埑偑壗V偺帪偵廃攇悢偑壗Hz曄壔偡傞偐偲偄偆娭學偑傢偐傟偽忋婰幃傪妶梡偱偒傞傢偗偱偡丅 忋婰偺幃惗惉偺棳傟偱曄挷攇傪COS偲偟偰偄傞偺偼埲壓偵帵偡棟桼偵傛傞偨傔偱偡丅 捠忢偺 analog VCO偼捈棳揹埑傕偟偔偼LFO側偳偺掅懍偺 CV傪梌偊偰摦嶌偝偣傞傛偆偵側偭偰偄傑偡丅丂偙傟偵懳偟偰 FM曄挷偱偼 audio懷堟偱曄挷梡VCO傪巊梡偟傑偡丅丂VCO偼捠忢 CV傪揹棳偵曄姺偟偰 偦偺揹棳偱 capacitor傪廩揹偝偣丄偁傞僞僀儈儞僌偱曻揹偝偣傞偲偄偆摦嶌傪孞傝曉偟偰敪怳婍偲偟偰婡擻偟偰偄傑偡丅 偙偺堊 capacitor偺斀墳偼愊暘婍偲側傞偺偱 捈棳揹埑(揹棳)傪壛偊傞偲僺僢僠偑曄壔偡傞傢偗偱偡偑audio懷堟偺 CV偵懳偟偰傕CV傪揹棳曄姺偟偨曄挷攇傪愊暘偟偨傕偺偑 capacitor偺廩揹揹埑偵側傞堊椉幰偺娫偱埵憡偑90搙曄壔偟傑偡丅丂傛偭偰 曄挷攇偑 SIN攇偱偁偭偨応崌丄廩揹揹埑偼 -COS攇偵側傝傑偡偺偱丄忋婰偺愢柧偱巊偭偨傛偆偵僉儍儕傾偺SIN攇偵懳偟偰SIN攇偱曄挷傪偐偗偨寢壥偺攇宍偑摼偨偄応崌偼丄偁傜偐偠傔曄挷攇偑COS攇 偵側傞傛偆偵椉幰偺埵憡傪儘僢僋偟側偗傟偽側傝傑偣傫丅 偝傜偵愊暘婍傪捠偭偨曄挷攇偺怳暆曄壔傪旝暘偟偨傕偺偑僉儍儕傾攇宍偺恑峴偵塭嬁傪梌偊傞偺偱 曄挷攇宍 ---> 愊暘 ---> 旝暘 --> 偲偄偆娭學偵側傝傑偡丅
偨偲偊偽曄挷攇偑COS攇側傜 忋婰偺椺偱旝暘寢壥偑SIN攇偺応崌偨偲偊偽僉儍儕傾丄儌僕儏儗乕僞廃攇悢偑摨偠帪丄曄挷寢壥偺攇宍偼帪娫曽岦偵旕懳徧側備偑傫偩攇宍偵側傝傑偡丅丂COS攇帪偼嫎攇偺傛偆側帪娫幉曽岦偵懳徧側攇宍偱偡丅
偙傟偵懳偟偰埲壓偵帵偡Phase Modulation偼曄挷攇偺壛嶼偵懳偟偰偼愊暘梫慺偑側偔愊暘梫慺偼僉儍儕傾偺埵憡恑峴偵嵺偟偰偺摍懍墌塣摦梫慺偺傒偵愊暘梫慺偑惗偠傑偡丅
|
Frequency modulation 偲 phase modulation偺堘偄
digital VCO
digital FM偱偼敪怳婍偵憡摍偡傞晹暘偵 VCO傪僔儈儏儗乕僩偟偨峔惉偺傕偺偲丄扨弮偵巒傔偵帵偟偨 捈慄忋徃偺僌儔僼偵曄挷攇傪僾儔僗偡傞傛偆側峔惉偵偟偨傕偺(偄傢備傞 phase modulation)偲偑峫偊傜傟傑偡丅
digital VCO偺峔惉椺傪埲壓偵帵偟傑偡丅丂 偙傟偼嵟廔揑偵偼 ROM 儊儌儕乕偵奿擺偝傟偨 SIN攇僨乕僞傪冇偱撉傒弌偡峔惉偺VCO偱偡偑丄偙偺応崌 埵憡偺恑峴偼 Z^-1偺 digital抶墑慺巕偲壛嶼婍偲婣娨儖乕僾偱峔惉偝傟偨愊暘婍偱偡丅偙傟偑phase accumulator 偲偟偰婡擻偟傑偡丅愊嶼抣偑偁傞抣傪挻偊傞偲phase accumulator偼reset偝傟傞偨傔偙偺嫇摦偲偟偰偼SAW攇偲偄偆偙偲偱偡丅
曄挷攇CV傕僉儍儕傾 CV偲摨偠壛嶼婍傪棙梡偟偰偄傞偨傔丄偙偺愊暘婍偺塭嬁傪 analog VCO偲摨條偵庴 偗偰偟傑偄傑偡丅
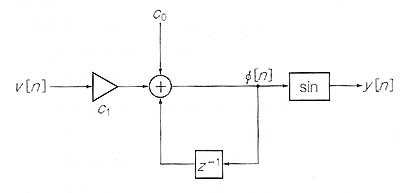
偙偺 digital VCO偱 帺暘偺弌椡偱曄挷傪偐偗傞丂self modulation傪偐偗偨偲偒偺弌椡攇宍偲丄愊暘嶌梡傪庴偗偨偁偲偺曄挷攇偺堦椺傪帵偟傑偡丅
僀儊乕僕恾
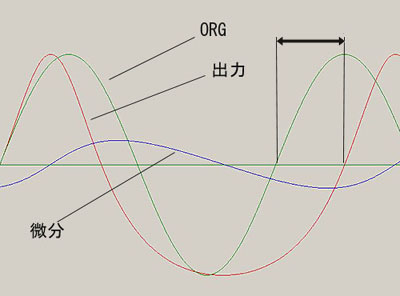
弌椡攇宍偼帪娫幉曽岦偵旕懳徧側惓尫攇丠偲偄偭偨姶偠偺攇宍偱偐偮廃婜偑戝尦偺僉儍儕傾怣崋偵懳偟偰 偺傃偰偄傑偡丅丂偮傑傝僺僢僠偑壓偑偭偰偄傑偡丅
傑偨愊暘婍丂捠夁屻偺曄挷攇宍(岎棳惉暘偺傒)偼-COS攇偺娫墑傃偟偨攇宍偵側偭偰偄傑偡丅丂偙傟傪 旝暘偟偨攇宍偑僉儍儕傾VCO(偙偺応崌偼僉儍儕傾丄儌僕儏儗乕僞偑摨堦偩偑)丂偵嶌梡偡傞傢偗偱偡偑偙偺攇宍偼 弌椡攇宍偲摨偠宍偵側傞傢偗偱偡丅(摉慠怳暆偼彫偝偄偱偡)
偙偺堊 惓尫攇偺+怳暆晹暘偱偼埵憡偑憗偔恑傒丄-怳暆晹暘偱偼埵憡偑抶偔恑傓偺偱偙偺傛偆側弌椡攇宍偑惗惉 偝傟傞傢偗偱偡丅
偱偼巆傝偺廃婜偑怢傃偰丄僺僢僠偑壓偑傞尨場偼偳偆偟偰偐偲偄偆偙偲偱偙傫偩偼愊暘婍捠夁屻偺慡晹偺 CV忣曬(僉儍儕傾偺弶婜敪怳廃攇悢愝掕梡捈棳CV傪娷傓)偺曄壔傪埲壓偵帵偟傑偡丅
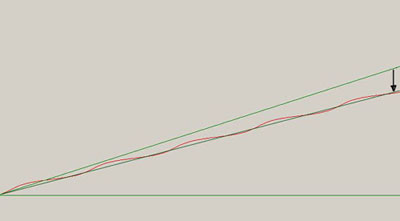
孹偒偺戝偒偄曽偺捈慄忋徃偼曄挷傪偐偗偰偄側偄帪偺曄壔丄 孹偒偺彫偝偄曽偼曄挷傪偐偗偨帪偺曄壔偱偡丅 丂屻幰偺応崌偼捈慄忋徃(捈棳CV)偵忋婰偺曄挷攇偑廳忯偝傟偨宍偵側偭偰偄偰偐偮捈慄偺孹偒偑掅壓偟偰偄傑偡丅丂 偡側傢偪偙傟偑僺僢僠掅壓偺尨場偲偄偆傢偗偱偡丅(儅僀僫僗 DC惉暘偑愊暘偝傟偰僆儕僕僫儖偺愊暘憹壛傪 墴偝偊傞)
忋婰偺旕懳徧曄挷攇(弌椡攇宍)偱偼儅僀僫僗晹暘偺柺愊偺曽偑戝偒偄偺偱 +, -偑僶儔儞僗偡傞 偨傔偵偼(AC僇僢僾儕儞僌偡傞偵偼)儅僀僫僗偺捈棳暘偑側偔側傟偽偄偄偺偱偦傟偑僉儍儕傾偺捈棳CV 偵壛嶼偝傟寢壥偑忋婰偺捈慄忋徃偺妏搙偵斀塮偝傟傞傢偗偱偡丅
< 愊暘偵偮偄偰 >
亄怳暆偲乕怳暆偺柺愊偑摨偠廃婜攇宍傪愊暘偡傟偽丄寢壥偼廃婜攇宍偵側傝傑偡丅丂
偟偐偟亄怳暆偲乕怳暆偺柺愊偑摨偠偱側偄廃婜攇宍傪愊暘偡傟偽亄偐乕偳偪傜偺曽岦偵敪嶶偟偰偟傑偄傑偡丅丂
偙偺敪嶶尨場偑捈棳僆僼僙僢僩惉暘偱偡丅
偮傑傝捈棳惉暘偲廃婜攇宍惉暘偑撈棫偵愊暘偝傟偨寢壥傪懌偟偨傕偺偑嵟廔寢壥偲側傞傢偗偱偡丅丂 忋婰偺椺偱偼曄挷攇偑扨撈偱愊暘偝傟傟偽丄廃婜塣摦傪偟側偑傜儅僀僫僗曽岦偵敪嶶偡傞傢偗偱偡丅
phase modulation
偙傟偵懳偟偰 僉儍儕傾CV擖椡偲曄挷CV擖椡偑暿宯摑偱擖椡偝傟傞峔惉偵偡傟偽丄曄挷攇偼愊暘婍偺塭 嬁傪庴偗側偔側傝傑偡丅丂傕偆彮偟惓妋偵尵偆偲忋婰偺 phase accumulator晹暘偵偼僉儍儕傾CV偺傒 傪偄傟傞偙偲偵偟偰埲壓偺傛偆偵偡傞偲尵偆偙偲偱偡丅
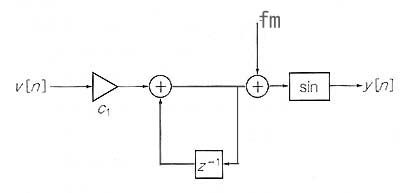
偙偆偡傞偙偲偵傛傝曄挷攇偼愊暘偺塭嬁傪庴偗傑偣傫丅丂偮傑傝婎杮揑偵偼僺僢僠傪惗傒弌偡梫慺偼 僉儍儕傾CV+phase accumulator晹暘側偺偱偡丅丂曄挷擖椡偵捈棳傪壛偊偨応崌傪峫偊傞偲偙偺応崌偼 忋婰偺VCO偺応崌偲堎側傝愊暘偝傟側偄偺偱抣偼堦掕抣傪曐偮偺偱扨偵弶婜埵憡偑偢傟傞偲偄偆堄枴 崌偄偵側偭偰捈棳偱僺僢僠偑曄壔偡傞偙偲偼側偔側傝傑偡丅
偮傑傝丄偙偺復偺堦斣弶傔偺埵憡恑峴偺捈慄忋徃偺恾偱捈棳怣崋偵憡摍偡傞曄挷攇傗丄+偲-偱柺愊偺堎 側傞曄挷攇傪廳忯偟偨応崌偲摨偠偵側傞傢偗偱偁傝丄丂E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) } 偙偺幃偲曄挷擖椡偺壛嶼曽朄偑摨偠偲偄偆傢偗偱偡丅
忋婰FM偺愊暘梫慺傪側偔偟偨曽幃偑 phase modulation偲偄傢傟傞傛偆偱偡丅丂 偮傑傝丂E(t)=SIN乷 2兾Fcl*t + a*SIN(2兾fm*t) } 偲偄偆偙偲偱偡(a偼掕悢(曄挷偺怺偝))丅
扨弮偵儌僕儏儗乕僞偺曄挷傪壛嶼偟偨宍丅
FM偲 PM偵偮偄偰傕偆彮偟峫偊偰傒傑偡丅
FM曄挷偱僉儍儕傾偲儌僕儏儗乕僞偺廃攇悢傪摨偠偔偟偰丄椉幰偺廃攇悢傪僔儞僋儘偝偣側偑傜廃攇悢傪 棊偲偟偰偄偔偲廃攇悢偑掅偄傎偳曄挷搙偑憹偟偰暋嶨側攇宍偵側傝傑偡丅
愊暘宱楬傪捠偭偨曄挷攇偼廃攇悢偑壓偑傟偽扨埵帪娫偁偨傝廩揹偝傟傞帪娫偑憹偊傞偺偱怳暆偑憹偊傞 偙偲偵側傝傑偡丅(廃婜偑巭傑偭偰偟傑偊偽捈棳偵側傞傢偗偱偡偹丅)丂 偱偡偐傜曄挷搙偼忋偑傞傢偗偱偡丅
偙傟偼偙偺復偺巒傔偺曽偱媈栤揰偲偟偰偁偘偨
E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) }丂丂偺幃偺捈棳偵懳偡傞懳墳偲偐偲偐傜傫偱偔傞傢偗偱偡偑丄弮悎 FM曄挷偱偼SIN(2兾fm*t)偑愊暘偝傟傞傢偗偱偡偐傜寢嬊 (1/fm)* cos(2兾fm*t)偲側傞傢偗偱偙偺 1/fm偵傛偭偰曄挷攇偺廃攇悢偑偝偑傟偽愊暘屻偺怳暆偼忋偑傞偙偲偵側傝傑偡丅
FM曄挷偺摦嶌偑忋婰偺幃偵曄姺偱偒傞偲偄偆偙偲偱偡偹丅丂 傛偔尒傟偽偙偺幃偼丂 FM偲偼曄挷擖椡偺壛嶼埵抲偑偙偲側傞堎側傞 phase modulation偺摦嶌傪偦偺傑傑嬶徾壔偟偨幃偱偁傞傢偗偱偡丅
偮傑傝曄挷攇偺曄挷搙僷儔儊乕僞偲偟偰偺(儮F/fm)傪庢傝嫀傞偲偄偆偐掕悢偵偡傟偽忋幃偼 phase modulation偦偺傑傑偺摦嶌偵側傝 1/fm 偱曄挷攇偺廃攇悢偱曄挷搙傪僗働乕儕儞僌 偡傞偙偲偱 FM曄挷偲摍壙偵側傞偲偄偆偙偲偱偡丅
丂丂* FM曄挷偺幃丂丂丂E(t)=SIN{ 2兾Fcl*t + (儮F/fm)* cos(2兾fm*t) }
丂丂* phase modulation偺幃丂丂丂E(t)=SIN{ 2兾Fcl*t + a*sin(2兾fm*t) }
偙偙偱 a:=儮F/fm傪戙擖偡傞偲忋婰幃偼丂FM偲摨偠偵側傝傑偡丅丂 扐偟偙傟傜偺幃偼fm=0偲側傞捈棳偺応崌偵偮偄偰偼摦嶌傪偆傑偔昞尰偱偒傑偣傫偲偄偆偙偲偱偡丅
忋婰偺傛偆偵 FM偲PM偱偼 曄挷攇偑 COS偲 SIN偲堎側偭偰偄傑偡丅丂丂傛偭偰 PM偱惗惉偝傟傞僉儍儕傾 偲 FM偱惗惉偝傟傞僉儍儕傾傪摨偠攇宍偵偟偨偄応崌偼丂FM偺応崌 COS偱曄挷偡傞昁梫偑偁傝傑偡丅
埲壓偵 FM偱丂COS偲 SIN偱曄挷偟偨応崌偺攇宍偺堘偄傪帵偟傑偡丅
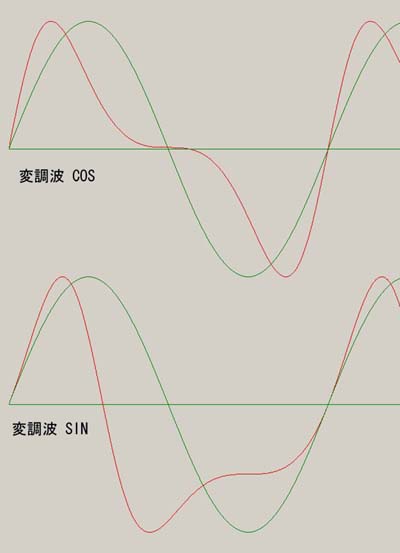
* FM壒尮偲攞壒
E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) }丂偺幃偐傜惗惉攇宍偺僉儍儕傾廃攇悢傪婎壒偲偟偨応崌偺攞壒峔惉傪昞偡幃傪摫偒偩偡偙偲偑偱偒傑偡丅丂偙偺幃傪 side band(懁攇懷)偺奺崁偺揥奐幃偲偟偰昞偡偲
E(t)= J0(m)仏sin(2兾Fcl*t)
丂丂丂 + J1(m){ sin[2兾(Fcl+ fm)]t - sin[2兾(Fcl- fm)]t }
丂丂丂 + J2(m){ sin[2兾(Fcl+2fm)]t + sin[2兾(Fcl-2fm)]t }
丂丂丂 + J3(m){ sin[2兾(Fcl+3fm)]t - sin[2兾(Fcl-3fm)]t }
丂丂丂 + ................
丂丂* Jn(m) ... 儀僢僙儖娭悢丅
丂丂* m ....... modulation INDEX m=儮F/fm
偲側傝傑偡丅(幃偺惗惉夁掱)丂
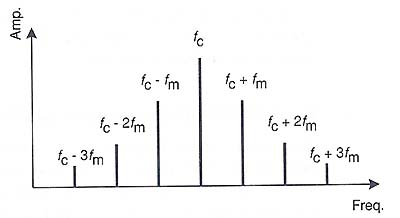
* side band 偺僀儊乕僕
戝尨懃偲偟偰丂side band 偼 僉儍儕傾廃攇悢傪拞怱偲偟偰 Fcl+fm , Fcl+2fm ....
Fcl-fm , Fcl-2fm....偲椉幰偺榓丄嵎惉暘偺廤傑傝偲側傝傑偡丅丂4徾尰偺AM曄挷偱偼 side band偼 Fcl+fm,
Fcl-fm偺 2偭偱廔椆偱偡偑 FM曄挷偱偼 嵎丄榓偲傕桳尷屄偱偼偁傝傑偡偑懕偒傑偡丅
奺攞壒峔惉梫慺(partial)偺娫妘偼曄挷攇偺廃攇悢偑崅偄傎偳峀偔側傝傑偡丅
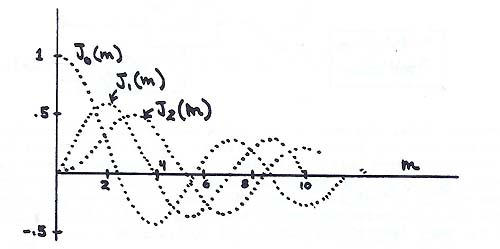
* 儀僢僙儖娭悢
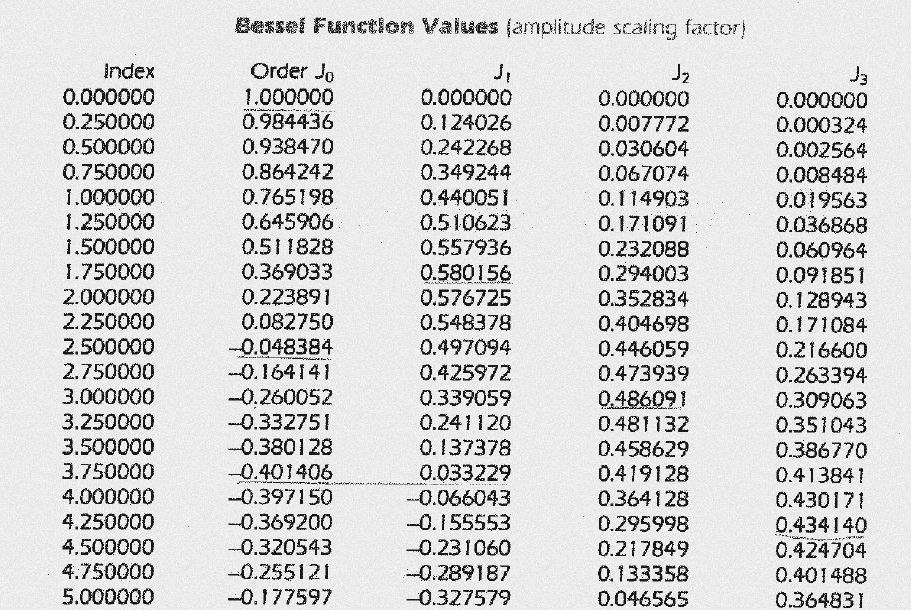
*儀僢僙儖娭悢昞(Index偼0.25扨埵偲偟偰偄傞応崌偺昞乯
side band偺峔惉梫慺偺奺崁(partial)偺怳暆偼忋恾偺儀僢僙儖娭悢偵傛偭偰媮傔傑偡丅
偨偲偊偽 J1(m)偺 partial偱偼偦傟偵憡摍偡傞儀僢僙儖娭悢傪慖傫偱丄儮F/fm偱媮傔偨m偺抣偵
奩摉偡傞X幉偺抣偐傜懳墳偡傞y幉偺抣傪媮傔偦傟傪怳暆偺學悢偲偟傑偡丅
忋恾偐傜傢偐傞傛偆偵儮F/fm偺抣偑戝偒偄傎偳 m 偼戝偒偔側傝傑偡偺偱婎壒偵懳偡傞攞壒偺 娷傒曽偺妱崌偑憹偊傑偡偟丄偦傟偑恑峴偟偰偄偗偽攞壒孮偺怳暆偺榓偺曽偑婎壒傛傝戝偒偔 側傞偺偱寢壥廃攇悢偼婎壒偺僺僢僠傪曐偰側偔側傝傑偡丅
偙傟偼僉儍儕傾偺廃攇悢偲曄挷攇偺廃攇悢偑惍悢攞偺娭學偵偁偭偰傕m偑偍偍偒偗傟偽僺僢僠 偼曄壔偡傞偲偄偆偙偲偱偡丅丂 偙傟偩偲偪傚偭偲榖偑柕弬偟偰偟傑偄傑偡偹丅丂偦偺傛偆側忬懺偵側偭偰偄傞帪偼曄挷攇偺 儅僀僫僗懁偺怳暆偑僺乕僋偵側傞埲慜偱 Fcl-fm偑儅僀僫僗偵側傞丄偮傑傝曄挷攇偺儅僀僫僗惉暘 偲摨偠怳暆偺儅僀僫僗偺捈棳傪偐偗偨寢壥偑 0Hz埲壓偵側偭偰偟傑偆傛偆側忬懺偱寢嬊丄曄挷攇宍 偑怳暆曽岦偵旕懳徧偵側偭偰偄傞偲峫偊傟偽偮偠偮傑偑崌偆傛偆偵巚偄傑偡丅
偄偔偮偐偺椺傪峫偊傑偡丅
僉儍儕傾偲曄挷攇偺廃攇悢偑摨偠帪偨偲偊偽 440Hz偺帪丅
僉儍儕傾傛傝戝偒偄廃攇悢偺side band偵懳偟偰忋婰幃偺奺崁偺廃攇悢偵偩偗拲栚偡傞偲丅
( Fcl+ fm) ....(Fcl+2fm).......偺崁)
*丂440+440=880 ............ 440*2
*丂440+880=1320 .......... 440*3
*丂440+1320=1760 ........ 440*4
*丂.....
( Fcl- fm) ....(Fcl-2fm).......偺崁)
*丂440-440=0 ................... 440*0
*丂440-880=-440=440 ......440*1
*丂440-1320=-880=880 .... 440*2
*丂.....
偲側偭偰僉儍儕傾廃攇悢偵懳偟偰 2,3,4,5.....攞壒偺側傜傃偵側傝傑偡丅 僉儍儕傾傛傝彫偝偄廃攇悢偺side band崁( Fcl- fm) ....(Fcl-2fm).......偺崁) 傕懚嵼偟偰偄傞偺偱 奺攞壒偵尒棫偰偨梫慺傪懌偟偨寢壥僾儔僗丄偙偺彫偝偄廃攇悢偺梫慺傪懌偟偨寢壥偑崌惉攇宍偱偡丅 ( 0Hz傛傝儅僀僫僗懁偵廃攇悢偑偒偨応崌偼僾儔僗埵抲偺梫慺偲壛嶼偟傑偡丅
儮F/fm偺儮F偺崁傪440Hz偲偟偨帪偺side band 偺奺崁 ( partial )偺怳暆傪儀僢僙儖娭悢偐傜媮傔偨昞傪 埲壓偵帵偟傑偡丅
*丂Fcl= 440Hz
*丂fm = 440Hz
*丂m=儮F/fm= 440Hz/440Hz=1
*丂僉儍儕傾(婎壒) .....0.77 *(440Hz)
*丂戞2攞壒丂 0.44* ((440+440=880) -(440-440)=0 )
*丂戞3攞壒丂 0.11 *((440+880=1320) +(440-880)=-440..婎壒 )
*丂戞4攞壒丂 0.02 *((440+1320=1760) -(440-1320)=880)
*丂.....
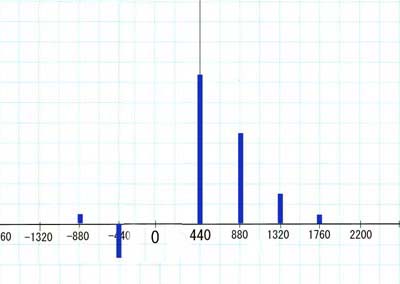
* 僔儈儏儗乕僔儑儞攇宍
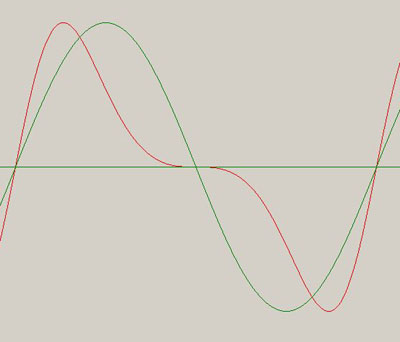
* 嵞崌惉攇宍(忋婰峔惉偱)
忋恾偼丂E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) } 偺幃偵抣傪偄傟偰攇宍傪昞帵偟偨椺偲丄儀僢僙儖娭悢偐傜媮傔偨怳暆偱丄攞壒壛嶼偵傛偭偰嵞峔抸偟偨攇宍偱偡丅丂攞壒偺悢傪尷掕偟偰偄傑偡偺偱姰慡偵摨偠攇宍偵偼側偭偰偄傑偣傫偑丄戝懱摨偠攇宍偱偁傞偙偲偐傜忋婰偺寁嶼丄夝庍偑娫堘偭偰偄側偄偙偲偵側傝傑偡丅
|
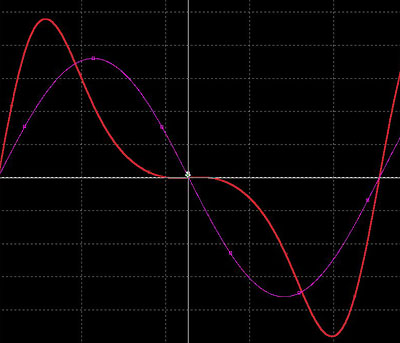
偙偺忬懺偼幃傪巊傢側偔偲傕姶妎揑偵棟夝偱偒傑偡丅丂曄挷攇偺旝暘攇宍偐傜丄僉儍儕傾攇偺1/2廃婜僞僀儈儞僌偱恑傒偲抶傟偑柍偔側傞偺偱偙偺僞僀儈儞僌偱柍曄挷偺僉儍儕傾攇宍偲曄挷帪偺僉儍儕傾攇宍偺怳暆偼摨偠偵側傝傑偨曄挷攇偺1/4廃婜偺僞僀儈儞僌偱曄挷搙=0偵側傞偺偱偦偺僞僀儈儞僌偱偺曄挷偝傟偨僉儍儕傾攇偲柍曄挷僉儍儕傾攇偺孹偒偼摨偠偵側傞偙偲偑傢偐傝傑偡丅
忋恾偵偍偄偰曄挷攇旝暘攇宍偺0偐傜90搙嬫娫偱偼柍曄挷僉儍儕傾偵懳憡庤曄挷偝傟偨僉儍儕傾偼孹偒(曄壔)偑媫 偵側傝90搙偐傜180傑偱偼媡偵曄挷偝傟偨僉儍儕傾偺曽偑孹偒偼娚傗偐偵側傝180搙偱曄壔=0偵側傝180搙偐傜360傑偱偼媡偺斀墳偵側傝傑偡丅 偡側傢偪曄挷偝傟偨僉儍儕傾攇偼90搙傪拞怱偲偟偨帪丄嵍塃偱旕懳徧側攇宍偵側偭偰偍傝敿廃婜偵偍偄偰攇宍偼旕懳徧偱嫎攇偵嬤偄儔儞僾攇忋偺攇宍偵側傞偙偲偼姶妎揑偵傕柧敀偵傢偐傞偱偟傚偆丅 忋婰偺椺偱偼敪怳廃攇悢偲嚈F偑摨偠抣側偺偱嵟戝偱880Hz帪偺孹偒偑摼傜傟傞億僀儞僩偑偁傝嵟彫偱0Hz偺孹偒偵側偭偰偄傑偡丅丂偱偼嚈F偑偦傟埲忋戝偒偄応崌偑偳偆側傞偺偱偟傚偆偐丠丅 |
曄挷搙傪攞偵偟偨応崌
*丂Fcl= 440Hz
*丂fm = 440Hz
*丂m=儮F/fm= 880Hz/440Hz=2
*丂僉儍儕傾(婎壒) .....0.2 *(440Hz)
*丂戞2攞壒丂 0.59* ((440+440=880) -(440-440)=0 )
*丂戞3攞壒丂 0.37 *((440+880=1320) +(440-880)=-440婎壒 )
*丂戞4攞壒丂 0.15 *((440+1320=1760) -(440-1320)=880 )
*丂.....
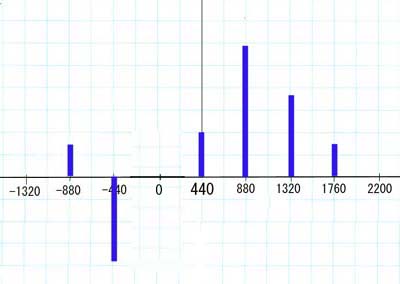
* 僔儈儏儗乕僔儑儞攇宍
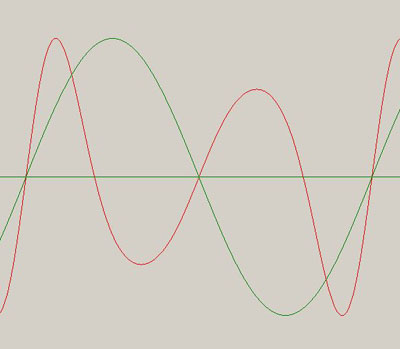
* 嵞崌惉攇宍(忋婰峔惉偱)
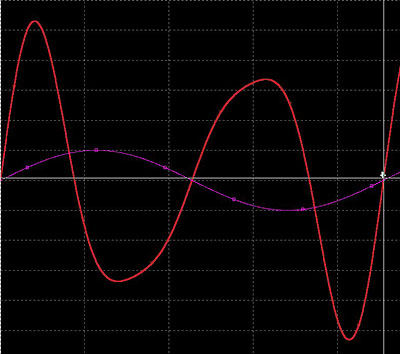
偙偺応崌偼曄挷攇偺儅僀僫僗晹暘偱夁曄挷偵側偭偰偄傞傛偆側忬懺偱偟傚偆偐丅丂 寢壥曄挷攇偑忋壓懳徧偵側傜偢丂DC僆僼僙僢僩偑僾儔僗偵側傝僺僢僠偼僉儍儕傾廃攇悢傪曐偭偰偄側偄丅
偱傕惗惉偝傟傞僉儍儕傾攇宍偼尦偺僉儍儕傾攇宍偺惍悢攞偵側偭偰偄傑偡偹丅丂側偵偐旈枾偑偁傝偦偆偱偡丅
僉儍儕傾偺廃攇悢 440Hz偱曄挷攇偺廃攇悢偑880Hz偺帪偼丄僉儍儕傾傛傝戝偒偄廃攇悢偺 side band偵懳偟偰
*丂440+880=1320 ....... 440*3
*丂440+1760=2200 ....... 440*5
*丂440+2640=3080 ....... 440*7
*丂.....
*丂440-880=-440=440 ...... 440*1
*丂440-1760=-1320=1320 ... 440*3
*丂440-2640=-2200 ........ 440*5
*丂.....
偲側偭偰僉儍儕傾廃攇悢偵懳偟偰 3,5,7,.....偺婏悢攞壒偺暲傃偵側傝傑偡丅丂摨條偵( Fcl- fm) ....(Fcl-2fm).......偺崁)偺崁傪懌偟傑偡偑丄抣偑 -440Hz, -1320Hz, -2200偲側傞偺偱晞崋斀揮偟偰傗傞偲傗偼傝婏悢攞壒偺側傜傃偵側傝傑偡丅
*丂Fcl= 440Hz
*丂fm = 880Hz
*丂m=儮F/fm= 440Hz/880Hz=0.5
*丂僉儍儕傾(婎壒) .....0.94*(440Hz)
*丂戞3攞壒丂 0.24* ((440+880=1320) -(440-880)=440丂)
*丂戞5攞壒丂 0.03 *((440+1760=2200) +(440-1760)=-1320丂)
*丂.....
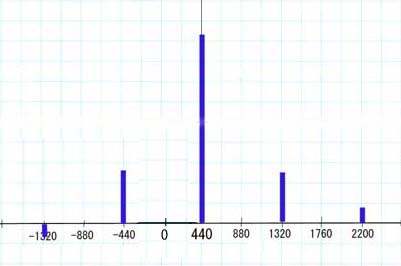
* 僔儈儏儗乕僔儑儞攇宍
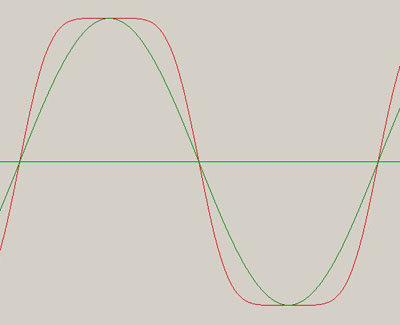
* 嵞崌惉攇宍(忋婰峔惉偱)
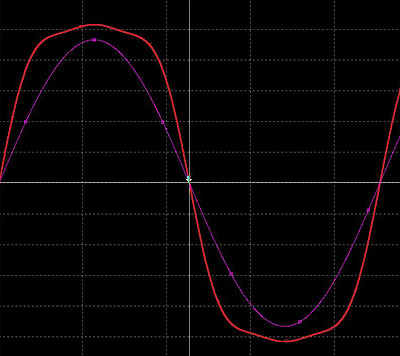
嵞崌惉帪偺攞壒悢偑彮側偄偺偱僔儈儏儗乕僔儑儞攇宍偲慡偔摨偠偵偼側偭偰偄傑偣傫丅
婏悢攞壒偺傒偺峔惉側偺偱嬮宍攇偵嬤偄宍偺攇宍偑惗惉偝傟偰偄傑偡丅丂儮F傪壓偘傟偽懳徧榗傒攇宍偲
側傝傑偡丅
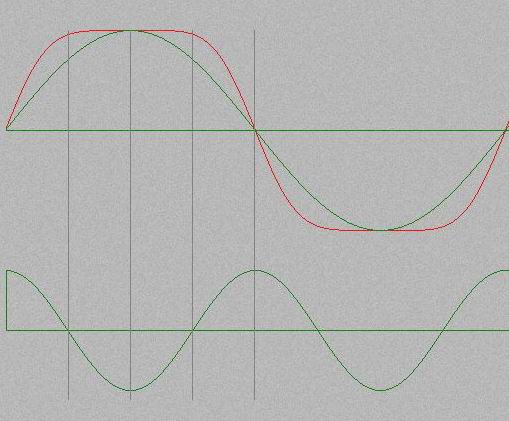 * 2攞偺廃攇悢偺曄挷攇偺旝暘抣(COS)偲弌椡攇宍偺娭學 僉儍儕傾偲曄挷攇偺廃攇悢偑摨偠応崌偲堎側傝忋婰偺応崌偼僉儍儕傾偺敿廃婜偵懳偟偰曄挷偝傟偨僉儍儕傾攇偼嵍塃懳徧偵側傝傑偡丅丂偙傟偼曄挷攇偺旝暘攇宍傪尒傟偽傢偐傝傑偡偑僉儍儕傾偺1/4廃婜偱曄挷攇偺恑傒丄抶傟偺愊嶼抣偼0偵側傝偙偺帪揰偱曄挷攇偺旝暘偺儅僀僫僗怳暆偼MAX偵側傞偺偱柍曄挷僉儍儕傾偺怳暆偲曄挷僉儍儕傾攇偺怳暆偑摨偠偱偐偮僉儍儕傾攇偺孹偒偼0偲側傝偦偙偐傜1/2廃婜傑偱偼媡曄壔偲側傞偺偱僉儍儕傾偺90搙傪拞怱偲偟偰嵍塃懳徧攇偑弌尰偡傞丅 傑偨曄挷攇偺90搙偺僞僀儈儞僌(僉儍儕傾偺45搙)偱曄挷攇偺怳暆=0偵側偭偰偄傞偺偱偙偺僞僀儈儞僌偱偺曄挷偝傟偨僉儍儕傾攇偺怳暆偲摨偠怳暆埵抲偵偁傞柍曄挷僉儍儕傾攇偺孹偒偼摨偠偵側傞偙偲偑棟夝偱偒傞偱偟傚偆丅 摉慠丄曄挷攇偺0偐傜90搙傑偱偺僞僀儈儞僌偱偼恑傒丄90搙偐傜180搙偺僞僀儈儞僌偱偼抶傟傪斀塮偟偰曄挷偝傟偨僉儍儕傾攇偺宍偑偱偒偁偑偭偰偄傑偡丅忋恾偼彮偟傢偐傝偵偔偄偺偱偡偑嵞崌惉帪偺恾傪尒傟偽偰僉儍儕傾偺45搙傛傝慜偲屻偱偼曄壔嬶崌偑戝暆偵堎側偭偰偄傞偺偑曄挷攇偺怳暆=0偺僞僀儈儞僌傪斀塮偟偰偄傞偙偲偑柧敀偵傢偐傞偲巚偄傑偡丅 偡側傢偪曄挷偝傟偨僉儍儕傾偺45搙埵抲偺怳暆偐傜僺乕僋怳暆傑偱偼傢偢偐側抣偱偁傝偦傟偵懳偟偰偦偙偐傜偼曄挷攇偺恑峴偑抶偔側傞僼僃乕僘偵側傞偨傔偝傜偵曄挷偝傟偨僉儍儕傾偺孹偒偼備傞傗偐偵側傝丄90搙埵抲偱曄壔偑柍偔側傝傑偡丅 嚈F偑傛傝戝偒偔側傟偽攇宍偺棫偪忋偑傝偼傛傝塻偔側傝嬮宍攇偵嬤偯偒傑偡偑夁曄挷偵側傞偨傔僉儍儕傾偺45搙丄135搙晅嬤偑傊偙傫偩宍偵側傝傑偡丅
|
忋婰偺椺偐傜攞壒偺婎杮峔惉偼僉儍儕傾偲曄挷攇偺廃攇悢嵎偱偒傑傝丄( side band偺暆傕)奺攞壒偺怳暆儗儀儖偼嶲徠偡傞儀僢僙儖娭悢偺埵抲偱寛傑傞偮傑傝儮F/fm偱偒傑傝傑偡丅儮F偼偮傑傞偲偙偲曄挷攇偺傾儅僂儞僩儗儀儖側偺偱偦傟偵傛偭偰壒怓丄僺僢僠偑曄壔偡傞偲偄偆偙偲偵側傝傑偡丅
曄挷攇偑僉儍儕傾偺廃攇悢偺 1/2偺応崌偼偳偆偱偟傚偆偐丅丂 僉儍儕傾440Hz丄曄挷攇 220Hz偺応崌傪峫偊傞偲 Fcl+fm=660Hz, Fcl-fm=220Hz偵側傝傑偡丅丂 偨偲偊偽曄挷搙 儮F=220Hz偲偟偨応崌丄
*丂Fcl= 440Hz
*丂fm = 220Hz
*丂m=儮F/fm= 220Hz/220Hz=1
*丂僉儍儕傾(婎壒) .....0.77*(440Hz)
*丂戞1.5/0.5攞壒丂 0.44* ((440+220=660) -(440-220=220))
*丂戞2.0攞壒丂丂丂丂 0.11 *((440+440=880) + (440-440=0))
*丂.....
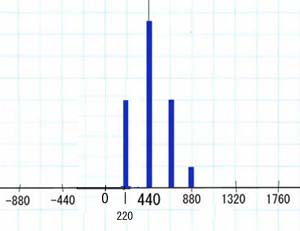
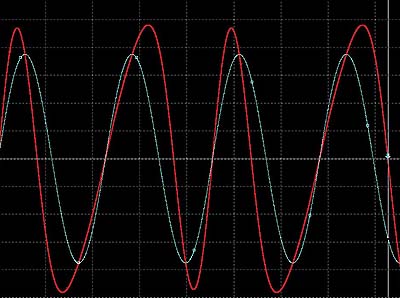
恾偐傜堦墳僺僢僠440Hz偵側偭偰偄傞偺偑傢偐傝傑偡丅丂 扐偟攇宍偵偼曄挷偑偐偐偭偰偄傞宍偵側偭偰婎壒偺2廃婜偱摨偠攇宍偑孞傝懼偊偡宍偵側偭偰偄傑偡丅丂 曄挷偵傛偭偰廃攇悢偑曄傢傟偽傑偝偵杮棃偺FM曄挷側偺偱偡偑偙偺応崌廃攇悢偼曄傢傜偢PWM偺傛偆偵埵憡 偑曄壔偟偰偄傑偡偺偱埵憡曄挷偲偄偆偺偱偟傚偆偐丅
偱偼660Hz偲220Hz偺梫慺偼偳偙偵徚偊偨偐偲偄偆偙偲偱忋婰偺梫慺偐傜傑偢 440Hz偲660Hz傪壛偊偨帪偺 僌儔僼傪埲壓偵帵偟傑偡丅
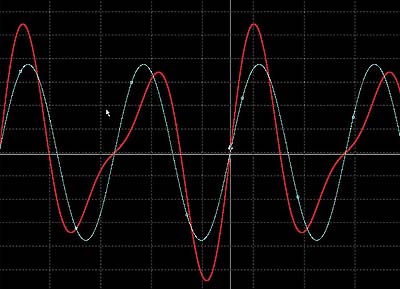
椉幰偑惍悢攞偺娭學偵側偄偺偱婎壒偺2廃婜偱摨偠攇宍偑弌尰偡傞宍偲側傝傑偨埵憡曄挷偲怳暆曄挷偑 偐偐偭偰偄傑偡偑廃攇悢偼440Hz偱偡丅丂 440Hz偲220Hz偺応崌偼偳偆偱偟傚偆偐埲壓偵偦偺傛偆偡傪帵偟傑偡丅
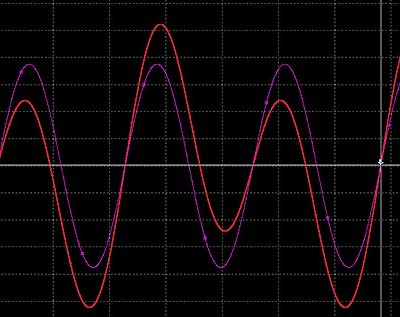
偙偺応崌傕摨條偵廃攇悢偼440Hz偱偡偑怳暆曄挷偲埵憡曄挷偑偐偐偭偰偄傑偡丅丂 寢嬊椉攇宍偺廃攇悢娭學偑妱傝愗傟傞抣偵偁傞帪偼崌惉寢壥偼怳暆偺戝偒偄曽偺廃攇悢偵側傞傛偆偱偡丅
傛偭偰慡 partial傪懌偟偨攇宍傕婎壒偵憡摍偡傞440Hz偺怣崋偲偟偰擣幆偝傟傞偙偲偵側傝傑偡偑丄
660Hz偲220Hz偺 partial 偺塭嬁偼埵憡曄挷偲怳暆曄挷偵側偭偰昞傟偰偄傑偡丅丂
曄挷攇偲僉儍儕傾偺嵎偑傕偭偲憹偊傟偽價僽儔乕僩偺傛偆側攇宍偵側傞偺偱偟傚偆丅
|
嶲峫:
E(t) = SIN{ 2兾*Fcl*t + (嚈F/fm)* SIN( 2兾*fm*t) }
壛朄掕棟偐傜
傛偭偰
偙偙偱
傑偨 傛偭偰埲壓偺揥奐幃傪摼傞丅
E(t)= J0(m)仏sin(2兾Fcl*t)
|
Linear FM 偲 exponential FM
analog FM偵栠偭偰丄linear FM偱偼曄挷攇偑僉儍儕傾偺惍悢攞偵偁偭偰曄挷攇偺怳暆曄壔偺 + 偲 - 偺榓偑0偱偁傟偽僉儍儕傾偺僺僢僠偼曄壔偟傑偣傫丅丂偙傟偼忋婰偺愢柧偐傜傕柧傜偐偱偡偑丂1廃婜撪偱埵憡偺恑傒抶傟偑憡嶦偝傟傞偺偱晹暘揑偵攇宍偑曄宍偟偰傕1廃婜偱傕偲偵傕偳傞偲偄偆傢偗偱偡丅
堦曽 exponential FM丂偮傑傝懡偔偺 analog synth偱昗弨揑偵巊傢傟偰偄傞 oct/V 偺 CV 巇條偱偼丄 oct/V 偺僉儍儕傾敪怳婍傪曄挷偡傞応崌丄僉儍儕傾偲儌僕儏儗乕僞偺敪怳廃攇悢偑惍悢攞偺娭學偑偁偭偰傕僺僢僠偼曄挷攇偱曄挷偟偨帪偲偡傞慜偱偼曄壔偟偰偟傑偄傑偡丅
偙傟偼寢嬊忋婰偺忦審拞偺怳暆曄壔偺旝暘攇宍偺 + 偲 - 偺榓偑0偵側傜側偄偐傜偱偡丅丂偮傑傝 oct/V偺CV擖椡偵擖傟傞慜傑偱偼 +,-偺怳暆攇宍偑摨偠曄挷攇偱偁偭偰傕 antilog amp傪捠偣偽丄儕僯傾側曄壔偑壒奒偺曄壔偵捛廬偝偣傞傋偔摍斾偺娭學偵曄姺偝傟傞傢偗側偺偱 +, - 1V偺曄挷攇偑 偨偲偊偽丂-1V帪 220Hz, 0V偱 440Hz, 2V偱880Hz偲偄偆僺僢僠曄壔傪傕偨傜偡傢偗偱擖椡偝傟偨曄挷攇偺旝暘攇宍偺+ , -偺柺愊偑堎側傞偙偲偵側偭偰偟傑偆偺偱僺僢僠偑曄壔偟偰偟傑偆傢偗偱偡丅
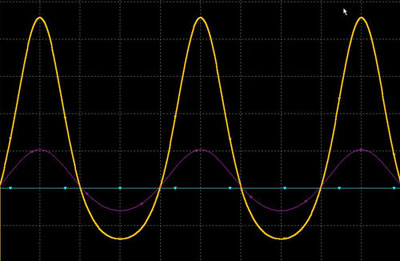
* antilog 捠夁屻偺曄挷攇偺椺
偙傟偼暿偺妏搙偐傜傒傞偲偙偺旕懳徧惓尫攇偺DC暘傪偲傝偺偧偔傋偔僆僼僙僢僩偑敪惗偟偰偦偺寢壥捈棳儗儀儖偑曄摦偟偰偦偺捈棳偑僉儍儕傾VCO偺 CV偵壛嶼偝傟僺僢僠偑曄傢傞偲傕偄偊傞偱偟傚偆丅
梫偼廃攇悢偺儕僯傾側曄壔偵懳偟偰壒奒偼摍斾曄壔側傢偗偱偁偭偰丄偦傟敪惗偝偣傞偨傔偺 oct/V VCO偼儕僯傾側曄壔偱偼側偄偲偄偆棟桼偱偁傞傢偗偱偡丅
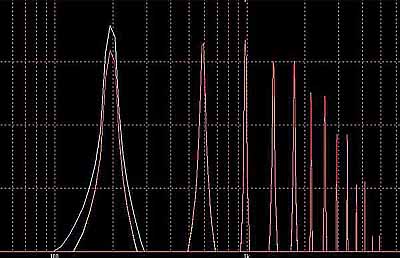
* linear FM ... FM曄挷偟偰傕婎壒(忋恾偺偄偪偽傫戝偒偄嶳)偼摦偐側偄丅
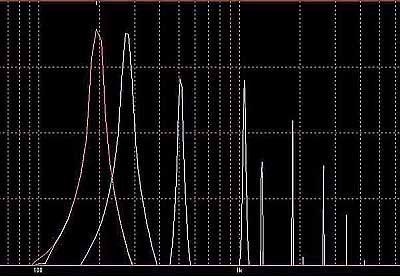
Expo FM ...FM曄挷偡傞偲婎壒(忋恾偺偄偪偽傫戝偒偄嶳)偺僺僢僠偑忋徃偟偰偟傑偆
| Analog VCO偺Hz/V擖椡傪巊偆偲Digital偺FM偵嬤偄摦嶌偑偱偒傞傢偗偱偡偑偙傟偩偗偱偼摦嶌偼晄姰慡偱偡丅偡側傢偪忋婰偺夁曄挷摦嶌傪幚尰偡傞偨傔偵偼敪怳曽岦傪媡夞揮偡傞昁梫偑偁傝傑偡丅丂偙偺傛偆側媡夞揮摦嶌偑壜擻側VCO傪Thru ZERO VCO偲屇傃傑偡丅 |
FM偲phase modulation偺堘偄
師偵嵞搙丄 side band(懁攇懷)偺奺崁偺揥奐幃偵拲栚偟偰傒傑偡丅

* 儀僢僙儖娭悢
E(t)= J0(m)仏sin(2兾Fcl*t)
丂丂丂 + J1(m){ sin[2兾(Fcl+ fm)]t - sin[2兾(Fcl- fm)]t }
丂丂丂 + J2(m){ sin[2兾(Fcl+2fm)]t + sin[2兾(Fcl-2fm)]t }
丂丂丂 + J3(m){ sin[2兾(Fcl+3fm)]t - sin[2兾(Fcl-3fm)]t }
丂丂丂 + ................
忋幃偐傜 曄挷攇fm偺廃攇悢偑0偵側傟偽攞壒偺敪惗偡傞崁偑側偔側傝丄傑偨儮F/fm偺崁偑亣偵側傞偺偱m 偑亣偵側傝奺paratial偺怳暆偼0偵側傞堊丄柍曄挷偵側傝傑偡丅丂phase modulation偱捈棳偱偼僺僢僠 曄壔偑側偄偲偄偆偙偲偺棟桼偵傕側傞傢偗偱偡丅
堦曽丄弮悎FM偺応崌傕偙偺幃偐傜攞壒偼側偄傢偗偱偡偑丄FM偼曄挷偵偐偐傢傞梫慺偑愊暘梫慺傪捠夁偡傞偺 偱曄挷攇偑捈棳偵側傟偽埵憡妏偺恑峴偼2兾(Fcl+fm)*t丂偲側傝丄曄挷攇偑廃婜傪傕偮応崌偼偦傟偑愊暘偝傟 傞偺偱偨偲偊偽COS攇傪擖傟傟偽SIN攇偵側傞傢偗偱偙傟偑椉幰偺堘偄偱偡丅
傕偆堦揰廳梫側偙偲偼丄
忋婰偺揥奐幃偐傜丄奺partial偺怳暆偵偐偐傢傞傢偐傞梫慺 Jn(m)偺 m傪曄挷攇廃攇悢偵偐偐傢傜偢堦掕抣偵
偟偨応崌偑 phase modulation偺杮棃偺幃偵側傝傑偡丅丂傛偭偰丄
*1:丂僉儍儕傾廃攇悢偲曄挷攇偺廃攇悢斾傪摨偠偵曐偭偨傑傑廃攇悢傪曄壔偝偣偨応崌丅
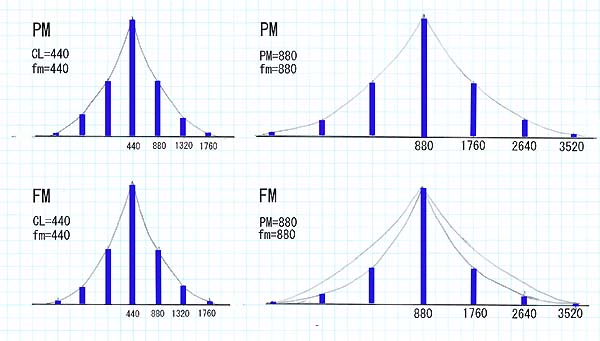
*丂phase modulation ---> 奺攞壒偺儗儀儖偼曄傢傜側偄丅
*丂FM 丂丂丂丂丂丂丂丂丂 --->丂廃攇悢偵奺攞壒偺儗儀儖偑曄壔丅
偲偄偆寢壥傪摼傑偡丅丂偙偺応崌 side band偺峔惉偑曄傢傜側偄偺偱 m偺抣偑曄挷攇偺廃攇悢偱曄壔偟側偄
phase modulation偼廃攇悢偑曄壔偡傞偲偄偆埲奜偵偼杮幙揑側曄壔偑偁傝傑偣傫丅
FM偺応崌偼 1/fm偺崁偑丂m偵嶌梡偡傞偺偱偦傟偵懳墳偟偨儀僢僙儖娭悢偺抣偑曄壔偡傞偺偱丄 奺partial偵懳偡傞怳暆偼曄壔偟傑偡丅 丂偍偍傓偹 m偑2埲壓偺斖埻偱偼廃攇悢偑掅偄傎偳攞壒偺怳暆偼崅偔側傝傑偡丅
壒尮偲偟偰偱偼側偔偰杮棃偺FM曄挷偱偼偙偺傛偆側巊偄曽偼偟側偄偺偩偲巚偄傑偡偑丄壒尮偲偟偰偺巊梡偱偼丄 僗儁僋僩儖偺帪娫曄壔偺側偄屌掕攇宍偲偟偰巊偆梡搑偱偼側偄偐偲巚傢傟傑偡丅丂偙偺応崌FM偱偼曄挷廃攇悢偱 僗働乕儕儞僌偝傟偰偟傑偆偺偱攇宍傪堦掕偵曐偪偨偄応崌偼丄傾儅僂儞僩儗儀儖傪 Key CV偱僩儔僢僉儞僌偡傞 昁梫偑偁傝傑偡丅
偙傟偑Hz/V analog syth CS30偺Linear FM婡擻偵偍偄偰modulator level偵懳偟偰VCA傪夘偟偰Key CV偵傛傞 Key tracking傪偟偰偄傞棟桼偐偲巚傢傟傑偡丅
偙傟偵懳偟偰丄
*2:丂僉儍儕傾廃攇悢屌掕偱曄挷攇偺廃攇悢傪曄壔偝偣偨応崌偼丄
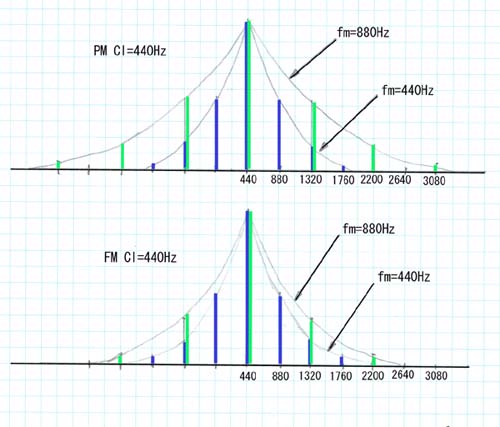
*丂phase modulation ---> 奺partial偺怳暆傪崌寁偟偨抣偼曄傢傜側偄丅
*丂FM 丂丂 ---> 奺partial偺怳暆傪崌寁偟偨抣偼曄挷廃攇悢傪崅偔偟偨曽偑掅偄丅
* 忋婰偺傛偆偵side band偺奺partial偺怳暆抣傪崌寁偟偨抣( sideband power distribution 偲偄偆傒偨偄
偱偡偑 )偑 FM偱偼曄挷攇偺廃攇悢偑崅偔側傞偲彫偝偔側傝傑偡丅丂梫偼慜偺寢壥偲摨偠偲偄偆傢偗偱偡丅
偙傟偼暿偺尒曽偱偼 side band偺暆偲偄偆偐峀偑傝 (total bandwidth... 偙傟傪曄挷搙偲偄偆丠) 偑 FM偱偼戝暆偵偼曄壔偟側偄偑 phase modulation偱偼曄挷攇偺廃攇悢偑掅偔側傞偲嫹傑傞偲偄偆偙偲偱偡丅
偱偡偐傜 phase modulation偱偼 曄挷廃攇悢偑0偮傑傝捈棳偺帪 side band偺暆偼0偱 怳暆偼桳尷抣 ( 帪娫偵娭學側偔堦掕抣 )側偺偱捈棳偱偼曄挷偝傟側偄偺偱偁傝丄FM偺応崌偼 side band偺暆偑嫹傑傞 偵偮傟偰奺 partial偺抣偑忋偑傞偺偱side band偺峀偑傝偼偁傑傝曄壔偟側偄丅丂 曄挷廃攇悢偑0偵側傟偽怳暆抣偼嵟戝( 帪娫亣偱怳暆傕亣 )偵側傞偺偱偡丅
偮傑傝捈棳偑堄枴傪帩偭偰敪怳偵娭梌偟偰偟傑偆偲偄偆偙偲偱偡..... 愊暘婍偺敪嶶偩偐傜丂 filter偺pole偲杮幙揑側堄枴偼摨偠偱偡偹丅
壛偊偰摉慠側偑傜曄挷攇偺廃攇悢偑曄壔偡傞偲(Fcl+fm)偺抣偑曄壔偡傞偺偱奺partial偺暆偑曄壔偟偰 僉儍儕傾傪婎壒偵傒偨偰偨応崌偺攞壒偺峔惉偑曄壔偟傑偡丅
偙偺復偺巒傔偺曽偱帵偟偨丂E(t)=SIN乷 2兾Fcl*t + (儮F/fm)*SIN(2兾fm*t) }丂偲偄偆堦偮偺幃偑
旕忢偵懡偔偺梫慺傪娷傫偱偄傞偲偄偆偙偲偑偍傏傠偘側偑傜傢偐偭偨傛偆側婥偑偟傑偡丅
寢嬊偺強Analog VCO偼昁慠揑偵愊暘梫慺傪 撪書 偟偰偄傞偺偱 phase madulation偼尨棟揑偵偱偒偢analog乮 Linear乯FM偺傒偑壜擻偲側傝傑偡丅傑偨phase modulation偵偍偄偰偼曄挷偺怺偝偺僷儔儊乕僞傪嚈F/fm偵抲偒姺偊傞偙偲偱FM曄挷偲摨偠幃偵側傞偺偱攇宍偺曄宍偲偄偆堄枴偱偼僺僢僠曄摦偺尦偺捈棳梫慺偑敪惗偟側偄傑偨曄挷攇傪COS攇偵偡傞昁梫偺柍偄phase modulation偺曽偑埖偄傗偡偄偲偄偆偙偲側偺偱偟傚偆偐丅
<2019/08/11 rev0.2>
<2018/12/03 rev0.1>
<2003/11/30 rev0.0>