差動(増幅)回路のからくり

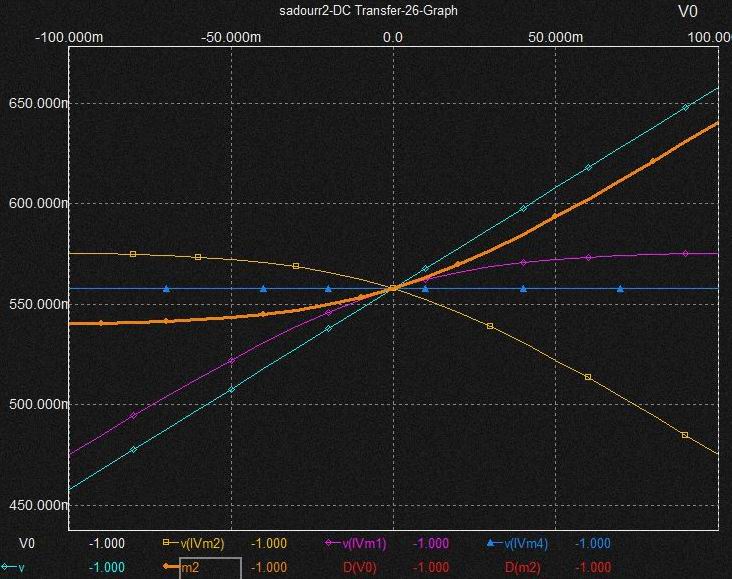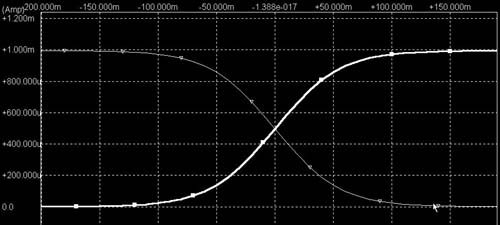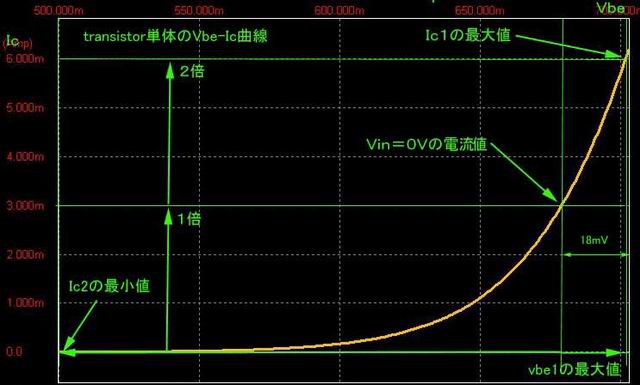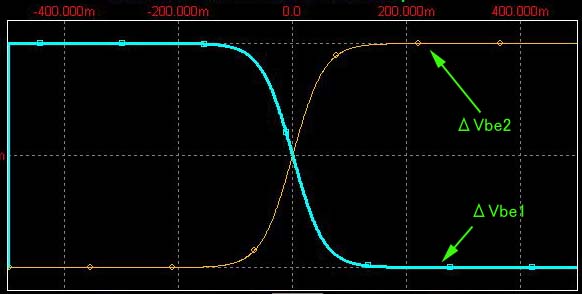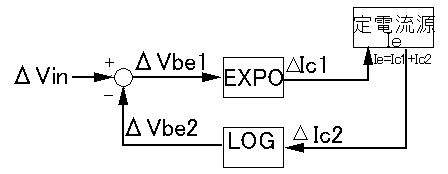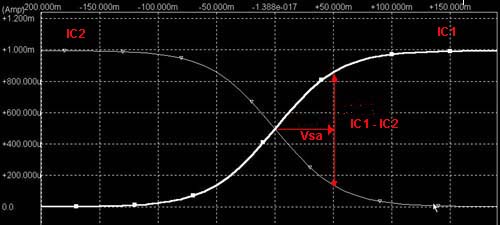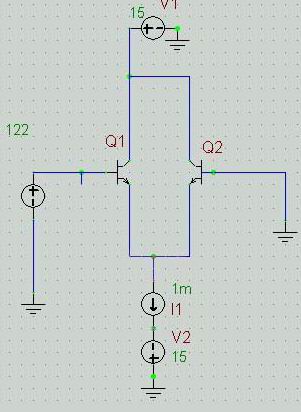
差動増幅では定電流源により増幅器の増幅要素のひとつであるgmを変えられる。　またこの定電流源があるので新たにB-E間をバイアスする必要は無い。　ベースに加える印加電圧の変化に対してIcの変化はEXPOにはならずかといって単純な直線変化になるわけでもない(直線変化の範囲はわずか)。　印加電圧の+/- 振幅変化に対してIc1、2の変化は対称である。　このことから印加電圧はQ1のB-E間のみににダイレクトにかかるのではなくさらにQ2のB-E間に対しても影響を与えていることがわかる。
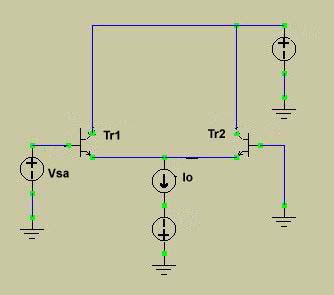
差動回路においては Q1, Q2が定電流源Ieを共有している。　そのため、印加電圧Vin（上図ではQ1のBに印加する電圧。　Q2のBはGND）が増加してIc1がΔIc1増えるとIc2はそのΔIc1分低下してバランスしなければならない。　この動作を実現するためのフィードバックループが差動回路の動作の本質です。
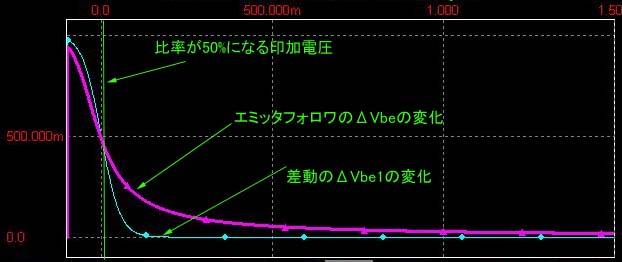
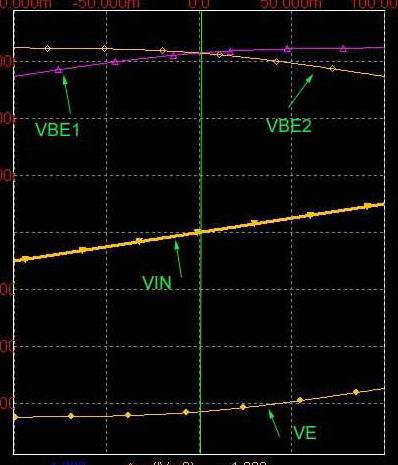
共有電流IeはQ1、Q2のB-E間微分抵抗の比で分流するため、Vinの増加でQ1の微分抵抗が低下してIc1が増えるとその分Ic2が減るようにQ2の微分抵抗が増加する為にはVbe2が低下することになります。　すなわち⊿Vinは Q1、Q2の両方のB-E間にかかる。　このためVinの上昇でVbも上昇すればVeも上昇し結果Vbe2は低下するわけですがこれは⊿Vinの分圧が逆方向にQ2のB-E間にかかるということ。(定電流源の端の電位は相手しだいなのでこの場合Veが上昇することがQ2に対して印加電圧が分圧されることを意味する。
差動増幅という意味はQ1とQ2のVbeの差を増幅するという意味である。　よってVb1とVb2の値を同じに保ちつつ( 両Tr. のベースに同じ電圧Vinをかける ) Vinの値を上昇させても微分抵抗比は変わらないのだからIc1,Ic2の変化は生じない。　すなわちVeがVinに追従して上昇して両Vbeは変化しないという一見不思議な反応、これもエミッタが定電流源につながっているからの反応。( Vbeが変化しないということはVeが上昇するということ)

上記のような負帰還反応によって印加電圧V1のごく小さな範囲においてはトランジスタのVbeとIcの間の非線形（EXPO)な特性が改善されリニアな特性になりさらに温度変化において上記の構造により両トランジスタの特性が同じであれば動作点の変動を防ぎ単体トランジスタのような温度変化の影響を受けにくくなる。

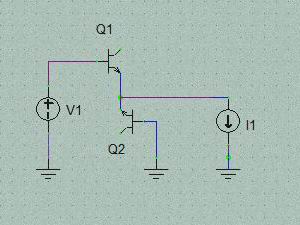
* 2っのTr.のVbeに印加される電圧の関係

上図において、Vin(上図ではV1)=0V時 Q1とQ2の Vbeは同じ条件になるため Ic1=Ic2となる。　この状態で Ic1,Ic2は定電流源の約1/2となります。　注意しなければならないのはVin=0Vで両transistorは活性化されており、Vin=0Vというのはこの場合はVbe1とVbe2の差が0Vということです。

Ic1,Ic2の最大値はこの値の2倍ですから、Vbe1,Vbe2の最大値は印加電圧=0V時のVbe1の値より最大約18mV(*0)しか変化できなくなるわけです。　すなわち Vin=0V以降、印加電圧Vinをどれだけあげても Vbe1の変化は 18mVに圧縮されてしまうということです。　残りの電圧はQ2のB-E間にかかる。　この場合当然Ve電位は固定でなく上昇変化しているということなのでVbe2はその分低下する。
*0: 電流が2倍になる為のVbeの変化量。

Ic1の上昇カーブは指数的に上昇するのではなく、指数的-->直線的-->対数的--->Ieの値に収束というカーブを取る。これはQ1とQ2の力関係でIcのカーブが変化すると言うことです。　正確には⊿Ic1=-⊿Ic2を実現する為のQ2による負帰還の強さ(⊿VinのQ2のB-E間にかかる逆方向の分圧の大きさ)によってIc1のカーブが変化します。
両者の特性が同じような範囲ではカーブは両者の逆特性によってリニアになりQ2の方が強い範囲（分圧比大）では本来のEXPOカーブがLOGカーブのように停滞してしまう。　この現象は定電流が両トランジスタに分流する際の両B-E間の微分抵抗の変化と考えるとわかりやすいです。
印加電圧Vinがマイナスの領域では⊿VinはQ1に多く逆方向でかかるので⊿VinがほぼQ1のVbeにかかっている形になりVinのリニアな変化に対してIc1はEXPOな本来な変化に近くなります。

Vinの分圧具合
水: Vin
桃: Vbe1
黄: Vbe2
橙: Vbe2の反転(Offset調整)
Vinの変化に対して Vin=0VでVbe2のカーブをあわせてさらに反転させるとVinに対するVbe1とVbe2の分圧の様子がよくわかります。　VinマイナスでVbe1が追従、Vbe2が停滞、Vinがプラスでは逆。　Vin= +/- 100mV以降ではVbe1,Vbe2は定常化(変化無しとVinに完全追従)。　Vin= +/- 20mV位の範囲が Vbe1とVbe2がほぼ逆特性カーブなので Ic1とIc2の変化がリニアになる。　その範囲を超えるとIcの分流は片方が変化がなくなりもう一方は - EXPO変化と言うトランジスタの Vbe - Ic関係に戻るべく推移。

* 電流特性

⊿Vinに対するQ1のVbeの分圧具合をエミッタフォロワとの違いで考えるとエミッタフォロワは分圧の対象となるもう一方はReなので抵抗値固定で Vbe -Ib指数関係、またIeも同様なのでそれの負帰還による逆特性によって EXPO * LOG特性で最終的にはリニアな電流特性が生じます。
差動回路の分圧においてはReに該当するQ2のB-E間抵抗は固定でなく変化します。　また電流値が固定化されているので後には飽和し、結果リニアな区間は Vin=0V近辺のごくわずかな領域となります。

上図のようにエミッタフォロワにおけるΔVbeの変化はゆっくりであって、0に近づきはするが0にはならない（- EXPO変化)。　それに対して差動のΔVbe1の変化は上記のようにQ2のｒπ2の影響を受けるので急激であり0になる。　このためIcはエミッタフォロワの場合、上昇となり差動の場合収束となる（変化分が0になるのでIc1は加算されない）。

本質的な反応はQ1、Q2が定電流源Ieで駆動されているため⊿Ic1の上昇に対して同量の⊿Ic2の下降が起こる必然からそれを実現できるように⊿Vinが⊿Vbe1と⊿Vbe2に分圧されるということでその際Q1とQ2のB-E間に対して Vinの分圧は逆方向でかかります。

抵抗の直列回路の分圧とVbe1とVbe2
抵抗の直列回路において印加電圧は抵抗値の大きいほうによりかかる（より分配される）。Q!とQ2のB-E間にかかる分圧ぐあいはTr.の動作点が高い方がB-E間の微分抵抗が小さいのだから⊿Vinの分配は小さく動作点の低い方はB-E間の微分抵抗は大きいので⊿Vinの分配は大きい。
印加電圧が0Vの時、動作点が同じだから分圧比はQ1、Q2で同じ。Q1のベースは印加信号につながり、Q2のベースはGNDで固定。印加電圧が全てQ1にかかるのであれば共通電位のVeは変化がないが両B-E間抵抗の直列接続なので印加電圧はQ1、Q2のB-E間に分配され中点のVe電位が変化(*1)。
印加電圧がプラスになればVb1上昇でVeも上昇するが上昇幅が同じであればVbe1に印加電圧の変化が伝わっていないことになる。　よってVb1の変化に対してVeの変化はそれより小さい値で変位する。 Q2についてはVe電位があがることはVbe2が下がることになる。
⊿Vinの増加によって動作点が変化しQ1のB-E間微分抵抗は下がり、Q2のB-E間微分抵抗は上がるので印加電圧のB-E間にかかる分圧比はQ2の方が大きくなる。Q2はベース電位がGNDで固定であるからVeが上昇することはVbe2が低下してB-E間微分抵抗が大きくなりQ2のB-E間に逆方向にかかる印加電圧の分圧比も上がる。Vinのさらなる上昇に対してVeの上昇率はVinに追従していくのでVbe1は変化しなくなっていき逆に印加電圧はQ2のB-E間に全部かかるような状態になりVbe2はVinに追従して低下していく。これがIc1が増えれば、同量Ic2が減るという反応を生じさせるメカニズム。またVbeの変化に対するIcの変化はリニアでなくEXPOなのでそれを満足するように分圧比が反映される。

* Vin/Vbe1/Vbe2/VEの関係
*1:
Vin変化以前のVbeの積算値に対して⊿Vinが各B-E間にB-E間微分抵抗値に応じて分配されるイメージ。

* 印加電圧の分配

* Vinを変化させた時のQ1 VbeとIcの変化の関係
複数の素子が動いていても各素子の基本動作は素子単体時の特性で動いているわけなので、Q1においては上図のtransistor単体のVbe - Ic曲線において　差動増幅におけるVin=0V時と同じIcの値をかりに3mAとするとIcの値は0から6mA近くまで移動することになる。
Vinが上昇するほどQ1のB-E間に印加される電圧が減っていくのがわかると思います。 Q1とQ2に分配される電圧の比率は以下の図のようになります。　⊿Ic1=-⊿Ic2の関係を成り立たせるためにこれだけの比率さが生じるということ。
注意点はVbeの値はそれまでの積算値 + ⊿Vbeであってそれの⊿Vinに対する分配比が以下のグラフのようになることであって積算値では無い点。　積算値(動作点)のバイアス具合によって比率は変化しています。

* Q1/Q2の動作点移動における⊿Vinの分圧比

印加電圧は　一見、Q1だけに作用しているように見えるが、上記のように　Q1の B-E間だけでなく、Q2のB-E間にも作用している。　ただし印加電圧はQ2の B-E間に対しては逆方向にかかる。(ベースがGNDなので)（定電流源は高インピーダンスなのでこの場合つながっていないのと同じ）
この差動増幅回路も一種の負帰還回路である。すなわち Vinが増加してVbe1が増え、Ic1がtransistor本来の指数的に増大しようとするとIc2が急激に減ろうとするわけで、Ic2の減少はQ2のVbe2を低下させこれはQ1のエミッタ電位を上昇させQ1のB-E間にかかる電圧を低下させるように働く（のでVbe1の変化は抑えられる)。

このため Ic1は急上昇できずゆるやかな上昇になり、Q2においてはIcの指数曲線を下降する方向に動いているのでΔIc1と同じだけの-ΔIc2を得る為にはVbe2の変化は大きくならなければならない。　このことは同時にΔVinの配分をΔVbe2よりにすることで実現される。　すなわちΔVbe1はΔVbe2の負帰還により小さくなっていく。

*差動回路の負帰還の構造
⊿Ic1が急激に増加しようとするとその分⊿Ic2が低下しそれに見合う分⊿Vbe2が低下しその分が⊿Vinから引かれ⊿Vbe1の分配が抑制されるので急激な⊿Ic1の増加はおこらないような関係で平衡する。
定電流源の必然から⊿Ic1の増加に対して同量の -⊿Ic2変化はLOG変換され⊿Vbe2の低下となる。　最終的に⊿Vbe1のEXPO変換で⊿Ic1が増加、⊿Ic2の低下をLOG変換した値の⊿Vbe2の低下分が⊿Vinからさし引かれた値が⊿Vbe1となる。

この回路はまたQ1,Q2のB-E間微分抵抗ｒπ(*1)の比で定電流が分流する回路でもある。　だからVbe1とVbe2が同じ値で変化するのならIc1,Ic2は変化しないわけである。
*1:　このｒπというのは微分抵抗であるから　単純に印加電圧の分割比と抵抗値の比が同じになるわけではなく、Vbe - Ic曲線の傾きの逆数であり微分抵抗です。
* ｒπ=hFE/gm
　ｇm=(q/KT)*Ic　----->常温でｇm=Ic/26m
　ｒπ = hFE / (Ic/26m)

* 計算式 *

PN junctionの基本性質の式と定電流源（Io）の関係からカーブが導き出されます。
*　Ic2＝Is＊exp(Vbe2/Vt).....Tr1に基本式を適用
*　Ic1＝Is＊exp(Vbe1/Vt).....Tr2に基本式を適用
*　Io=Ic1+Ic2..............................定電流源との対応
*　Vsa=Vbe1-Vbe2.....................印加電圧
*　　-Vsa=-(Vbe1-Vbe2)=Vbe2-Vbe1
*　　Vt=kT/q　(熱電圧)　常温で26mV　
Ic1/Ic2=exp((Vbe1-Vbe2)/Vt) .....指数の性質から式を変形
Ic1=Ic2(exp(Vsa/Vt).......................Vsaを代入
Ic1=Io-Ic2............................................Io=Ic1+Ic2 より
Io-Ic2=Ic2(exp(Vsa/Vt)
Io=Ic2(1+exp(Vsa/Vt)
* Ic2=Io/1+exp(Vsa/Vt)
Ic2/Ic1=exp((Vbe2-Vbe1)/Vt)
Ic2=Ic1(exp(-Vsa/Vt).....-Vsaを代入
Ic2=Io-Ic1
Io-Ic1=Ic1(exp(-Vsa/Vt))
Io=Ic1(1+exp(Vsa/Vt)
* Ic1=Io/(1+exp(-Vsa/Vt))

Ic1とIc2は以下のようになり、
* Ic1=Io/(1+exp( -Vsa/Vt))
* Ic2=Io/(1+exp( Vsa/Vt))
Vbe1=Vbe2=0Vの時 Ic1=Ic2=Io/2となります。
計算上は Io=Ic1+Ic2　、Vsa=Vbe1-Vbe2　という条件とtransistorの裸特性で上記式が得られる。
印加電圧に対する出力電流特性(Ic)のグラフを以下に示します。

* 出力電流特性　Ic1(太白)　Ic2(白)　(X軸:印加電圧)

transistorの特性と Ieを両transistorが共有するという条件を与えれば、計算式からはわりと簡単に特性が得られるのでわかったような気がしてしまいますが、なかなかこれだけでは本質がわかりませんね。

* gm と増幅率 *

差動増幅ということで、こんだは増幅について考えます。　入力電圧に対する出力電流の関係を相互コンダクタンス(transconductance)　 gm といいます。　この場合差動出力におけるgmはΔ(Ic1-Ic2)/ΔVsaです。
Vsaが0から+Vsaだけ変化した時のIc1-Ic2というのは上図の通りですから、
Ic1-Ic2=Io/{1+exp(+Vsa/Vt)} *2ということになります。　よってgmは、
　gm=Δ(Ic1-Ic2)/ΔVsa　=　d/dx{ 2Io/(1+exp(+vsa/Vt)}
　　　=(-2Io/Vt)*{{exp(+Vsa/Vt)}/{(1+exp(+Vsa/Vt)}^2}
展開して絶対値を取って　(2Io/Vt)* {{exp(+Vsa/Vt)}/1+2{exp(+Vsa/Vt)}+exp(+2Vsa/Vt)}
Vsa=0の時の接線の傾きは Io/2Vt となるので、上記カーブの直線性が確保されている範囲での　gm =Io/2Vtとなります。
シングル出力時は Io/4*Vtです。

コレクタ-+電源間に負荷抵抗Rcをつけた時のコレクタ-GND間の電圧をそれぞれVout1、Vout2とすると微小変化 ΔVout1とΔVout2は
　ΔVout1=(-Io*Rc/4Vt)*ΔVsa
　ΔVout2=(Io*Rc/4Vt)*ΔVsa
差動出力時はΔVout1-ΔVout2の絶対値=(Io*Rc/2Vt)*ΔVsa
よって、
　* シングル出力時の増幅度=Io*Rc/4Vt
　* 差動出力時の増幅度=Io*Rc/2Vt

上図のように印加入力電圧に対して出力のカーブは指数的変化、直線変化、対数的変化となり、直線性のよい部分は入力信号の0Vを中心としたわずかな範囲となります。

* 関係式から得られるもの

Q1はtransistorのVbeとIcの関係式、　Ic1=Isat(exp(Vbe1/Vt)　を満たして動作しているわけだが、Ic1とIc2の関係は以下のようにも表される(上の計算式の項参照)。
　Ic1=Ic2(exp(Vin/Vt)

これはtransistorの裸特性がIc2の変化により去勢されている状態を示している。
相手(Ic2)の特性にtransistor(Q1)の裸特性をかけると去勢された Q1の特性(Ic1)が出てくるというのは1次LPFにおいてHPFの電流特性をcapacitorの特性(積分)に入れるとLPFの電圧特性が出てくるのと同じようなもの。　どちらも相補的な特性を持つ。
上式のVinは印加信号電圧の変化そものなので (exp(Vin/Vt) はTr.の裸特性のEXPO変化でありそれにIc1の逆特性であるIc2をかけると相補的なIc1の特性が現れる。

ここでのIc2の変化というのはIeの分流比を反映しているわけで、Q2の分流比が大きいということは抵抗ｒπ2が小さいこと。　Ic2とIc1は相補的なカーブであるのでｒπ1とｒπ2も逆の関係になる。
このことはIc2が大きいときはQ1のrπ1も大きいということ、つまりΔVinのｒπ1 とｒπ2による分圧比の関係と同じであるということなので、Ic2のカーブはΔVbe1 の変化のカーブと同じ形ということになる。
exp(Vin//Vt)で得られるtransistorの裸特性が負帰還によってQ1のB-E間にかからなくなる具合をかけたということだから、上記の式はVinのかわりにQ1に実際に印加される電圧Vbe1でEXPOカーブを動かした場合と同じであるから、Ic1=Isat(exp(Vbe1/Vt)と同じということだ。
Ic2の変化、すなわちΔVbe1のカーブを積分したものがVbe1のカーブと形が同じになる。　Vinが十分マイナスにある時、Vbe1は直線上昇し、 Vinが0Vにもなると傾きがlog的な変化をし、さらにVinがあがると変化はさらにゆるやかになる。

<2023/04/26 rev0.5>
<2018/09/29 rev0.4>