ごく基本的なオブジェクト

このページは，下の画像のような形状をどうやって作るのかについてです。

box（立方体） sphere（球） cylinder（円柱）
cone（円錐） cone（円錐台） torus（トーラス）

大きさを分かりやすくするために，次の画像の上に立方体や球などを作っていきます。

立方体（box）

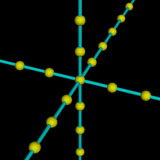
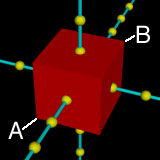
object {
	box { <-1, -1, -1>, <1, 1, 1> }
	texture { pigment { rgb <1, 0, 0> } }
}

「box { <-1, -1, -1>, <1, 1, 1>}」が立方体の形状を指定する部分です。box { } 内の最初の<-1, -1, -1>がAの座標，2番目の <1, 1, 1>がBの座標です。立方体はこのように，角の座標を二つ指定することでつくることができます。

球（sphere）

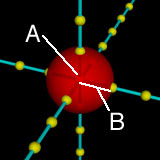
object {
	sphere { <0, 0, 0>, 1 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

「sphere { <0, 0, 0>, 1 }」が球の形状を指定する部分です。sphere{ } 内の <0, 0, 0>が球の中心（A）の座標，1が球の半径（B）です。

円柱（cylinder）

object {
	cylinder { <0, -1, 0>, <0, 1, 0>, 1 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

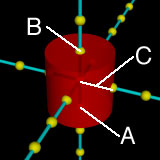
「cylinder { <0, -1, 0>, <0, 1, 0>, 1 }」が円柱の形状を指定する部分です。cylinder{ } 内の最初の <0, -1, 0>が円柱の底面の円の中心の座標（A），2番目の <0, 1, 0>が円柱の上面の円の中心の座標（B），最後の1が円柱の円の半径（C）になります。上面と底面とどちらを先に指定しても，結果は同じですが。

次のように書くと横向きの円柱になります。上向きの円柱を作っておいて，90度回転させたものと同じです。

object {
	cylinder { <-1, 0, 0>, <1, 0, 0>, 1 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

円すいと円すい台（cone）

円すいと円すい台はいっしょにみてみましょう。円すいは円すい台の特殊なケースと考えたほうがいいような気がしますので，まず円すい台からです。

object {
	cone { <0, 1, 0>, 0.5, <0, -1, 0>, 1.0 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

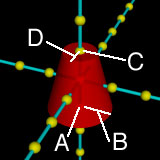
「cone { <0, 1, 0>, 0.5, <0, -1, 0>, 1.0 }」が円すい台または円すいの形状を指定する部分です。cone { } 内の「 <0, 1, 0>, 0.5」が円すい台の上面の円の中心の座標（A）とその半径（B），「 <0, -1, 0>, 1.0」が円すい台の底面の円の中心の座標（C）とその半径（D）になります。

このとき，上面の円の半径を0にすれば，下の画像のような円すいになります。

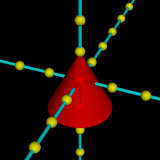
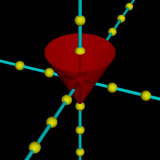
まあ上と下がどちらが広くてもOKなので，下のように書くと逆向きの円すいができます。上向きの円すいを作っておいて180度回転させたときと同じ形になります。

object {
	cone { <0, 1, 0>, 1, <0, -1, 0>, 0 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

上面と底面の半径を同じ値にすれば円柱になってしまいますが，これはあまり意味ないですね。

トーラス（torus）

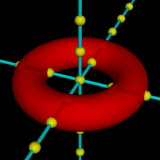
object {
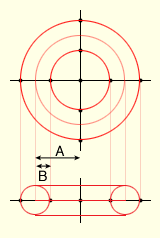
	torus { 1.5, 0.5 }
	texture { pigment { rgbf <1, 0, 0, 0.2> } }
}

「torus { 1.5, 0.5 }」がトーラスの形状を指定している部分です。torus { } 内の最初の数値が下の画像のA，2番目の数値が下の画像のBの値になります。原点を中心として円を1周させるとトーラスができますが，原点から円の中心までの距離がA，円の半径がBになります。

戻る