内分点と画像の拡大・縮小

＃４内分点と画像の拡大・縮小 2002.08.03（初版）2004.01.02（加筆）


　平面上に幾つかの点があって、これらの点をなめらかにつなぐ曲線を求めることを
補間といいます。つまり本来１つの曲線で表されるはずが、部分的な点しか分かって
いないとき、これらを元に不足した間の点を補って曲線を近似するのが補間です。

　ここでは最も簡単な線形補間を取り上げます。線形補間とは、点を折れ線で結ぶこ
とです。折れ線で近似とは何とも知恵のない話にみえますが、画像処理では強力な働
きをすることを以下で見てゆきます。

　２点間を線分で結んだとき途中の点は内分点になります。内分点は高校の数学で学
びます。
　この基礎事項が、画像の拡大・縮小を始め様々な画像処理で使われるアルゴリズム
の原理の１つです。


内分点

　まずは、内分点を求める式を導いておきます。



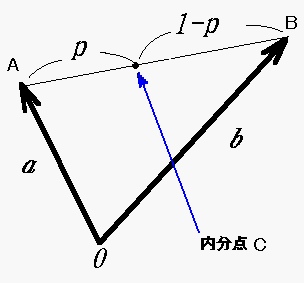　上の図で、点Ａ、Ｂを p:(1-p) に内分する点Ｃは次のようにして求まります。
ただし、pは０～１までの数です。

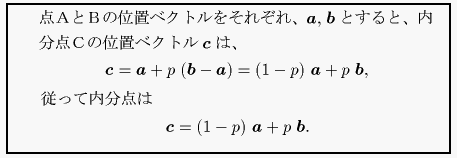　この式は、２つの点Ａ、Ｂの座標値を (1-p):p の割合で混ぜると点Ｃの座標値が
求まるという見方をすることもできます。この様な立場をとると、座標点だけではな
く座標ごとに値をもつ場の量に対しても使えます。
　例えば、大気の温度を地上からの高さ h の関数 T(h) で表すと、高さの差δが十分
に小さい２点間では、比 p:(1-p) に内分する高さの温度は

           T = (1-p) T(h) + p T(h+δ)

と線形近似することができます。

　これから考えるのは、画素（ピクセル）からなる座標での色データの関数を考えて、
i行j列の画素の色すなわちRGB値（Ｒは赤、Ｇは緑、Ｂは青の０～２５５の階調）を

            φ= φ(i,j),

と書くことにします。


画像の拡大（双線形補間）


　画像を拡大する場合を考えます。幅を zx倍、高さを zy倍すると、画像の画素数は拡大
した分増えますので、画素に隙間ができる格好になります。この隙間を補間して埋めるこ
とを考えます。
　それには、拡大した画像の座標値(i,j)から元の画像の対応する座標値(x,y)を座標変換
して求めます。変換は単なるスケール変換なので、拡大した倍率で割れば元の座標が求ま
って（つまり逆変換を行う）、

           x = i/zx,
           y = j/zy.

で与えられます。ここで (i,j) は画素の座標値なので整数値ですが、(x,y) は実数値にな
ることに注意しましょう。このとき、元の画像で (x,y) を囲む４つの画素の座標値を求め
ます。


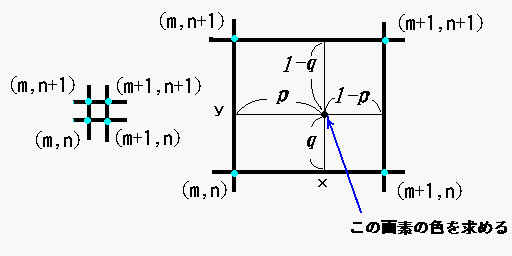　上の図に示すように、

        m <= x < m+1,  n <= y < n+1,

という関係を満たす整数 m,n を求めます。
　つまり、m は x の小数を切り捨てた整数値で、n は y の小数を切り捨てた整数値です。

　次に、点(x,y)の色φ(x,y)をこの点を囲む４つの画素の色

      φ(m,n),  φ(m+1,n),  φ(m,n+1), φ(m+1,n+1)

を使って、次のようにして線形補間して求めます。

これを双線形補間法といいます。以上で点(x,y)の色φ(x,y)すなわち拡大した画像での
点(i,j)の色φ(i,j)が求まりました。後はプログラムの実装です。


プログラム例


　完全なプログラムを示します。このプログラムは、Windows 95/98/2000 用の基本グラ
フィックス・クラスライブラリ GLIBW32 (ver 1.33以上)を使っています。
　また、このプログラムは画像の拡大と縮小の両方ができます。
// scale.cpp          (c) Yamada, K
#include "glibw32.h"

const int Xsize = 320, Ysize = 290; // ビットマップのサイズ

void scale(GRAPH&, GRAPH&, double, double);
void table(GRAPH& , int, int, int [2][2], int [2][2], int [2][2]);

int main()
{
    ginit(2*Xsize, Ysize);  // グラフィクス・ウィンドウを開く
    loadbmp("loadbmp.bmp"); // ビットマップのロード

    GRAPH g1,g2;
    g1.window(0, 0, Xsize-1, Ysize-1); // ロードした画像の座標
    g1.view(0, 0, Xsize -1, Ysize-1);
    g2.window(0, 0, Xsize-1, Ysize-1); // マッピングを行う座標
    g2.view(Xsize, 0, 2*Xsize-1, Ysize-1);

    // g1のピクセルをスキャンして、g2にマッピング
    scale(g1, g2, 2.0, 2.0); // 2×2倍に拡大する

    gend(); // グラフィクス終了

    return 0;
}

// オブジェクトg1の画像を拡大・縮小してオブジェクトg2にマッピング
// zx :幅の拡大・縮小率
// zy :高さの拡大・縮小率
void scale(GRAPH& g1, GRAPH& g2, double zx, double zy)
{
    int xs = Xsize/2;
    int ys = Ysize/2;
    int m,n;
    int R[2][2], G[2][2], B[2][2], r, g, b; //RGB値
    double x, y, p, q;

    for(int i = -xs; i < xs; i++){
        x = i/zx;
        if(x > 0) m = (int)x;
        else m = (int)(x-1);
        p = x - m;
        if(p==1){ p=0; m=m+1; }

        for(int j = -ys; j < ys; j++){
            y = j/zy;
            if(y > 0) n = (int)y;
            else n = (int)(y-1);
            q = y - n;
            if(q==1){ q=0; n=n+1; }

            if((m >= -xs) && (m < xs) && (n >= -ys) && (n < ys)){
                // 双線形補間
                table(g1, m+xs, n+ys, R, G, B);
                r = (int)((1.0-q)*( (1.0-p)*R[0][0]+p*R[1][0] )
                              + q*( (1.0-p)*R[0][1] + p*R[1][1]) );
                g = (int)((1.0-q)*( (1.0-p)*G[0][0]+p*G[1][0] )
                              + q*( (1.0-p)*G[0][1] + p*G[1][1]) );
                b = (int)((1.0-q)*( (1.0-p)*B[0][0]+p*B[1][0] )
                              + q*( (1.0-p)*B[0][1] + p*B[1][1]) );
            }
            else{
                r = g = b = 0;
            }  // 値が範囲外
            if( r < 0 ) r = 0; if( r > 255) r = 255;
            if( g < 0 ) g = 0; if( g > 255) g = 255;
            if( b < 0 ) b = 0; if( b > 255) b = 255;
            g2.pset(i+xs, j+ys, RGB(r,g,b)); // 補間した色で点を打つ
        }
    }
}

// (x,y)の周辺４画素の色を求める
void table(GRAPH& g, int x, int y, int R[2][2], int G[2][2], int B[2][2])  
{
    COLORREF crf[2][2]; // COLORREFはRGB値を４バイト整数で記憶するマクロ型
    for(int i = 0; i < 2; i++)
        for(int j = 0; j < 2; j++){
            g.getpixel(x+i, y+j, crf[i][j]); // 座標点の色を読み出す
            R[i][j] = GetRValue(crf[i][j]);  // Ｒ色の階調を取り出す
            G[i][j] = GetGValue(crf[i][j]);  // Ｇ色の階調を取り出す
            B[i][j] = GetBValue(crf[i][j]);  // Ｂ色の階調を取り出す
        }
}
プログラムでは、元になる画像を左半分に読み込み表示して、右半分に拡大縮小して描き
ます。表示する範囲を扱いやすくするために、画像の中心が画素座標の原点になるように
扱っています。
　双線形補間する部分のコードは、関数 scale() 内にあります。それほど複雑なコード
ではありません。


実行結果


　プログラムを実行した結果を下に示します。２×２倍に拡大した場合です。



拡大した画像は、なめらかに色調が変化していて上手くいっています。

　縮小した結果を下に示します。



縮小の場合も、上手く描かれていて成功といえるでしょう。

以上、画像の拡大・縮小の実行ファイルとソースファイルのダウンロードはこちらです、

画像の拡大と縮小
実行ファイル、ソース・ファイルと画像ファイル
Windows 95/98/2000 上で動作します。 　　ダウンロード
　　scale.lzh (205KB)

更に進んで 　以上のことが理解できれば、いろいろな画像変形も同じ手法でできます。要は、元の画像と変形した画像との間で座標変換を正しく定義することです。上の拡大・縮小プログラムでいえば、(i,j)から(x,y)への逆変換です。　以下の例は実行結果だけを示します。プログラミングの演習問題として挑戦してみてください。　１つ目は画像を４５°回転したものです。回転の場合も補間してマッピングする必要があります。単純に座標点を回転させるだけだと画素に穴が空いてしまうでしょう。　２つ目の例は、ＣＧの分野でテクスチャマッピング(texture mapping)と呼ばれるテクニックの典型です。　下は、背景画像を半球面上に貼り付けて、それを背景に射影するプログラムの実行結果です。MS Windows のスクリーンセーバーで、こんなのがディスプレイ内をうろうろと動き回るのがあるでしょう。テクスチャマッピング　高度な処理を行っている様にみえますが、拡大・縮小プログラムと本質的に同じです。違うのは座標変換のところだけです。実質的には数行程度書き換えるだけです。　この概念を理解するには、平面に描かれた世界地図から地球儀を描くことを考えることです。　平面の世界地図は緯度と経度の角度で描かれています。この２つの角度は３次元空間の球面上では極座標の２つの角度に対応しています。従って直角座標から、極座標への変換を定義して、その逆変換を行って描きます。 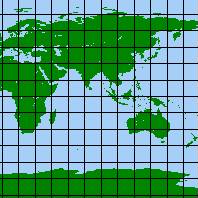== 変換 ==> 　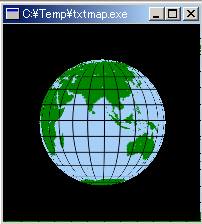上の右図は、そのようにして左の地図を球面に貼り付けて描いた地球儀です。分かってみると「なあんだ」というようなプログラムです。　次のページで簡単に解説します。

| 目次 | 次のページ |