 この図形は実軸(a軸)について対象(上下対象)です。つまり、a軸は左側のへこん
だ部分と右側の針の部分を結んだ線です。
この奇妙な球根を詳しく見るまえに、複素点列について意味を検討しましょう。点列
の初めの方は
この図形は実軸(a軸)について対象(上下対象)です。つまり、a軸は左側のへこん
だ部分と右側の針の部分を結んだ線です。
この奇妙な球根を詳しく見るまえに、複素点列について意味を検討しましょう。点列
の初めの方は
マンデルブロー集合とは、次のような複素数についての漸化式(点列)が、n → ∞ で発散しない(このことを有界といいます)ような、パラメータλの集合 です。λは複素数ですので、これを次のように表す(iは虚数単位)と
この集合は、横軸をa(実数軸)、縦軸をb(虚数軸)にとった平面内の図形としてあ らわされます。次の図の黒い部分がそうです。
この図形は実軸(a軸)について対象(上下対象)です。つまり、a軸は左側のへこん だ部分と右側の針の部分を結んだ線です。 この奇妙な球根を詳しく見るまえに、複素点列について意味を検討しましょう。点列 の初めの方は
となります。各zは複素数なので、
と表すことにします。 λが実数の場合(つまり b = 0)は、zの値はすべて実数値(つまり y = 0)とな ります。これを横軸をλ(つまりa)にとり縦軸をxにとって、この点列の挙動をプロ ットしましょう。漸化式を解くアルゴリズムは単純で、次の擬似コードで表現できます。
void mandel_plot(double a, double b)
{
double x = 0.0, y = 0.0, x1, y1;
for(int n=0; n < NMAX; n++){
x1 = x * x - y * y -a;
y1= 2.0 * x * y - b;
if( x1*x1 + y1*y1 > 4.0 ) return; // 発散
if( n > 500 ){
位置(a,x1)に点を打つ;
}
x=x1; y=y1; // 点列の更新
}
} |
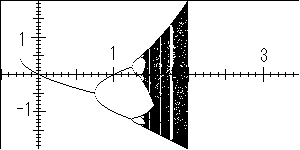 計算では、点列を1000点まで計算して後半の500点をプロットしています。図の
左側から始まる一本の線は、1点に収束していることを意味します(これを吸引不動点
といいます)。その後、この線は2つに分岐します。これは2点間を交互に移り変わる
ことを意味します(周期2)。それから4つに分岐(周期4)します。分岐は、2のべ
きの周期に分岐して、やがて複雑に入り込んだ挙動をします。点が密になっているとこ
ろはカオス帯とよばれます。その中で、白く抜けた帯状の部分は「窓」とよばれます。
また、左端と右端の途切れた領域は、発散(±∞)を意味します。
つまり、マンデルブロー集合には、(1)1つの点に収束する。(2)有限個の点の
間を行き来する(周期振動)。(3)有限の領域内を不規則に動き回る(カオス)。の
3つの挙動を示します。
またこの集合は、|λ| ≦ 2 、つまり半径2の円内にあることが分かっています。こ
のことから、繰り返し計算で、zが半径2の円を超えるとその点列は発散すると判定で
きます。この判定条件を使って上のコードでは
if( x1*x1+y1*y1 > 4.0 ) return; // 発散
と、捨てています。
さて、この分岐の挙動とマンデルブロー集合の領域との対応を示したのが次の図です。
計算では、点列を1000点まで計算して後半の500点をプロットしています。図の
左側から始まる一本の線は、1点に収束していることを意味します(これを吸引不動点
といいます)。その後、この線は2つに分岐します。これは2点間を交互に移り変わる
ことを意味します(周期2)。それから4つに分岐(周期4)します。分岐は、2のべ
きの周期に分岐して、やがて複雑に入り込んだ挙動をします。点が密になっているとこ
ろはカオス帯とよばれます。その中で、白く抜けた帯状の部分は「窓」とよばれます。
また、左端と右端の途切れた領域は、発散(±∞)を意味します。
つまり、マンデルブロー集合には、(1)1つの点に収束する。(2)有限個の点の
間を行き来する(周期振動)。(3)有限の領域内を不規則に動き回る(カオス)。の
3つの挙動を示します。
またこの集合は、|λ| ≦ 2 、つまり半径2の円内にあることが分かっています。こ
のことから、繰り返し計算で、zが半径2の円を超えるとその点列は発散すると判定で
きます。この判定条件を使って上のコードでは
if( x1*x1+y1*y1 > 4.0 ) return; // 発散
と、捨てています。
さて、この分岐の挙動とマンデルブロー集合の領域との対応を示したのが次の図です。
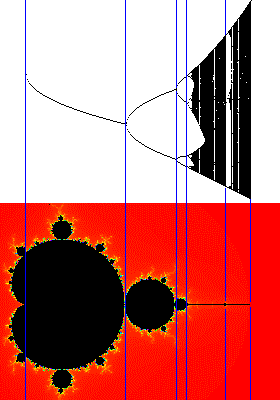 実軸(a軸)に沿って、3つの黒い球根の大きい順にそれぞれ不動点、周期2、周期4
となって、針の部分がカオス帯となっているのが分かります。また詳しく見ると、針の
部分に団子のような小さな球があり、この領域は周期3の「窓」に対応していることが
分かります。カオスの中にも更に構造があることが伺えます。
実軸(a軸)に沿って、3つの黒い球根の大きい順にそれぞれ不動点、周期2、周期4
となって、針の部分がカオス帯となっているのが分かります。また詳しく見ると、針の
部分に団子のような小さな球があり、この領域は周期3の「窓」に対応していることが
分かります。カオスの中にも更に構造があることが伺えます。
分岐図の実行ファイルとソースファイルのダウンロードはこちらです、
| マンデルブロー集合 (1)分岐図
実行ファイルとソース・ファイル Windows 95/ 98上で動作します。 |
mandel01.lzh (73KB) |
* このソフトウェアは、SYMANTEC. NORTON AntiVirus 5.0 でウィルス検査を 行っています。 * ファイルは吉崎栄泰氏による LHA (Copyright(c)1988-92 H.Yoshizaki)を 使って圧縮しています。
Copyright(c) 2000 Yamada,K