区別の仕方を変えると？（円順列、重複順列、組み合わせ）

区別の仕方を変えると？

「順列」や、「組み合わせ」では、並べる物の種類が全て違い、並べる方向は一定である場合を考えていました。
今度は、区別のしかたを変えた、次のような場合を考えてみます。

1.並び方の「方向」を区別して並べる（円順列）
2.同じ物は区別しない（重複順列、組み合わせ）
3.全く区別しない。

　　　　　3番はtrivialすぎてどうしようもないですよね。
なにも区別しないなら、並べないのと同じことです。
　　　　　つまり、１通りしかない。

では、以降で１と２について詳しく見ていくことにします。

1.並び方の「方向」を区別して並べる（円順列）

　　　　　順列では、例えばa,b,cの3つを並べるとすると、
　　　　　(a,b,c),(a,c,b),(b,c,a),(b,a,c),(c,b,a),(c,a,b)の６種類があります。

ですが、丸テーブルに並んで腰掛けるとすると、
(a,b,c)と(b,c,a)と(c,a,b）は区別がつかないことがわかります。

よくわからない人は、果物でも丸く並べてみて、自分が時計回りに回ってみてください。
別の並び方になっていても、実際には果物の位置は変わっていません。
なぜなら、「並べ替えていない」からです！

だから、(a,b,c)の文字をずらすと(b,c,a)と(c,a,b）になる、と考えられます。

では、(a,b,c)と(c,b,a)の二種類を考えてみましょう。
これらの文字をずらすと同じ物になるでしょうか？
答えはNoです。二つ目を1文字ずらすと(a,c,b)となって同じにはなりません。

実際、丸く並べた果物のうち、どれか二つを交換すると、
前とは違う並び方になりますよね。

このような並べ方の数は、(n-1)!で計算できます。
　　　　（裏返して重なる並び方があれば、(n-1)!/2とすればいいわけです。）

2.同じ物は区別しない（重複順列、組み合わせ）

それでは、同じ物は区別しない場合を考えてみましょう。
　　　　　順列は意外に簡単です。n^r.で計算できます。

つまり、これまでは、以前に並べたものと区別しなければならなかったため、
1ずつ引いた物をかけていたのですが、これからは、べつに何個とってもかまわないので、
　　　　　以前にどれを選んでも、次の選び方は、全部から選べるということなのです。

しかも並べ方はあくまでも考えるので、（番号はついたまま）
同じ個数を、選ぶ回数だけかけていくわけですから、n^rになるわけですね。

では今度は、並べ方もどうでも良い場合を考えましょう。（重複組み合わせ）
　　　　　実は、これは思ったよりも厄介なのです。

　　　　　ふつうは、k種類のものからn個を選ぶという重複組み合わせを考えるとき、
　　　　　n個+（k-1個のしきり)　から　k-1個のしきりをとると考えます。
　　　　　これは、k種類のものは、k-1個に区切れるから、その区切り方も全体の数にいれてやろうと考えるわけです。
つまり、しきりを入れて区別した後に、しきりと取っ払えばいいという考え方ですね。

　　　　　また、「ネットワーク型教材データベース　数学のいずみ」内の補足レポートによれば、
　　　　　種類ごとに項目分けしてしまえばいいとのことです。

　　　　　例として、3種類の物から10個とる場合を考えます。
1番目からm個とって、2番目からr個とって、また1番目からs個とって・・と繰り返して10個とればいいわけですね。

ここで、発想の転換。選び方は全部で30個あると考えます。
　　　　　種類をa,b,cとラベルづけすると、a、b、cのそれぞれが１０個ずつ選べるというわけです。

さらに、その10個を区別します。（ここがポイント）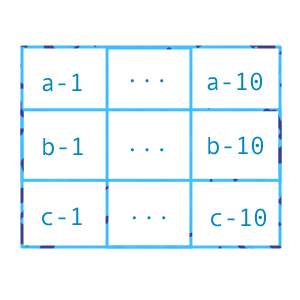

しかも、(a-1)を選ぶと(b-1),(c-1)は選べないと考えます。あくまでも前に進むしかないわけです。
（参考サイトでは、これを経路問題と呼んでいます）

わかりにくければ、取り出してから番号をつけると考えればいいでしょう。
いわば、番号の重複は許されないわけです。
あくまでも、1番目に選ばれたものは、種類に関わらず1番目に選ばれたもの、一つだけです。
もう一度取り出せば、それは２番目の物になってしまいます。

すると、始めに(a-1),(b-1),(c-1)の中から一つ選んだとすると、
次の選び方（縦2種類＋横10通り＝12通り）の中から、10通りを選べばいいわけですね。